Формула Байеса.

Весьма часто возникает следующая ситуация: до исследования мы имеем некоторые знания о вероятностях тех или иных событий, но под давлением вновь поступивших фактов вынуждены переоценить их. Как это сделать корректно? Ответ на этот вопрос даёт формула Байеса.

Первоначальные, "доопытные" вероятности называются априорными, а изменённые по результатам опыта - апостериорными. Теорема Байеса устанавливает количественную связь между ними.

Р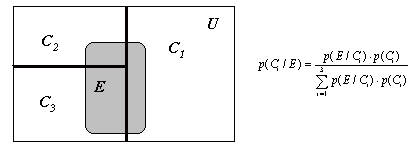 ис 5

Условия, при которых справедлива теорема Байеса, поясним следующим примером, которому соответствует рис.5.

Допустим, множество U разбито на три класса, то есть на три попарно несовместных события. Какое-нибудь из них обязательно происходит. Назовём их «конкурирующими причинами». Ещё есть событие Е, которое может происходить совместно с любой из «причин». Естественно назвать его «следствием». Вероятности известны. Условные вероятности - тоже известны. Допустим далее, что событие Е произошло. Ясно, что имело место и одно из событий С₁ , С₂ ,С₃ , но мы не знаем, какое именно. Спрашивается, как изменилось наше представление о том, что событие Е вызвала именно "причина" ? Другими словами, требуется оценить условную вероятность для всех значений i. Другими словами, требуется оценить -относительные площади пересечений на рис 5.

Событие Е можно представить как - то есть как объединение трёх пересечений. Вероятность его можно вычислить по формуле:

. Кроме этого, мы имеем тождество:

, откуда получим:

. (**)

Поскольку и числитель, и знаменатель последнего выражения известны, мы можем оценить искомые условные вероятности. Формула (**) и есть формула Байеса. Мы показали её справедливость для трёх конкурирующих причин, но она тривиально обобщается на любое их количество.

Пример. Пусть С₁ событие, заключающееся в наличии у данного человека туберкулёза, а С₂ – отражает отсутствие у него туберкулеза. Допустим, туберкулёзом болеет 0,5% населения. Значит, априорные вероятности . Пусть событие Е заключается в наличии затемнения флюорограммы. При наличии туберкулёза флюорограмма затемнена в 95% случаев, у нетуберкулезников - в 15% случаев (Это может быть вызвано погрешностями фотопроцесса или нарушениями в легких нетуберкулёзного характера).

Положим, некий человек сделал флюорограмму и на ней видно затемнение лёгких. Событие Е наступило. Как следует переоценить вероятности наличия и отсутствия у него туберкулёза?

Имеем: . По формуле Байеса получим:

.

То есть, затемнение флюорограммы заставляет считать, что вероятность наличия туберкулёза у пациента увеличилась от 0,5% до ~3,1%. То есть апостериорная (послеопытная) вероятность в шесть раз больше априорной (доопытной).

Случайные величины.

Случайной называется величина, которая с какой-то вероятностью принимает одно определённое значение из некоего диапазона. Понятие случайной величины в теории вероятностей не менее фундаментально, чем понятие вероятности.

Примеры.

Число посетителей данного магазина в течение рабочего дня;

число граммов сахара, проданных за этот день в этом магазине;

число ДТП со смертельным исходом, случившихся в регионе за квартал;

и тому подобное.

Следует всегда помнить, что

Появление различных значений данной случайной величины - попарно несовместные события:

магазин в день могут посетить 34 или 45 человек, но такой ситуации, когда магазин в течение дня посетило 34 и в тоже время 45 человек, быть не может.

Вопрос: если величина случайна, и мы не можем знать наперёд, какое значение она примет, то, что мы вообще можем знать о ней?

Ответ: мы можем знать вероятность её попадания в более или менее узкие диапазоны.

В наилучшем, предельном случае мы можем знать вероятность появления того или иного конкретного значения данной случайной величины.