
- •1. Общее представление об экономико-математическом моделировании
- •1.1. Определение экономико-математической модели
- •1.2. Классификация экономико-математических моделей
- •1.3. Основные этапы экономико-математического моделирования
- •2. Основы финансовой арифметики
- •2.1. Простой процент
- •Наращенная сумма при простом проценте
- •Текущая стоимость при простом проценте
- •Номинальная годовая процентная ставка
- •3. Математически методы анализа последовательностей платежей
- •3.1. Текущая стоимость последовательности платежей
- •3.2. Будущая стоимость последовательности платежей
- •3.3. Стоимость последовательности платежей в произвольный момент времени
- •4. Моделирование инвестиционных проектов
- •4.1. Дисконтирование денежных потоков инвестиционного проекта
- •4.2. Модель с постоянным процентным ростом свободных денежных потоков
- •4.3. Задача оптимального финансирования проекта
- •4.4. Задача оптимального выбора инвестиционных проектов
- •4.5. Анализ чувствительности денежных потоков проекта
- •4.6. Анализ безубыточности проекта
- •4.7. Влияние инфляции на денежные потоки проекта
- •4.8. Анализ финансового риска инвестиционного проекта
- •4.9. Имитационное моделирование денежных потоков проекта
- •5. Математические методы анализа платежей облигаций
- •5.1. Платежи облигаций
- •5.2. Доходность к погашению облигации
- •5.3. Текущая стоимость облигации
- •5.4. Продолжительность облигации
- •5.5. Чистые доходности
- •5.6. Использование чистых доходностей для оценки рыночной стоимости купонных облигаций
- •5.7. Синтетические бескупонные облигации
- •5.8. Описание оценки рыночной стоимости облигации в общем случае
- •5.9. Условия существования имитирующего портфеля и однозначности оценки рыночной стоимости облигации
- •5.10. «Чистые» коэффициенты дисконтирования, их нахождение и использование для оценки рыночной стоимости облигации
- •5.11. Нахождение чистых доходностей методом наименьших квадратов
- •5.12. Форвардные доходности
- •6. Моделирование процентного риска
- •6.1. Продолжительность и выпуклость портфеля облигаций
- •6.2. Чувствительность текущей стоимости портфеля облигаций к изменению доходности
- •6.3. Чувствительность собственного капитала финансовой организации к изменению доходности облигаций
- •6.4. Иммунизация будущих платежей от процентного риска
- •7. Моделирование кредитного риска
- •7.1. Использование линейной модели вероятности для оценки кредитного риска
- •8. Теория инвестиционного портфеля
- •8.1. Инвестиционный портфель и его основные характеристики
- •8.2. Диверсификация риска
- •8.3. Множество инвестиционных возможностей
- •8.4. Оптимизация инвестиционного портфеля
- •8.5. Множество инвестиционных возможностей при наличии безрисковой доходности
- •8.6. Оптимизация инвестиционного портфеля при наличии безрискового актива
- •8.7. Рыночная модель
- •8.8. Разложение общего риска финансового актива на систематическую и собственную составляющие
- •8.9. Модель оценки финансовых активов
- •9. Математические методы анализа финансовых производных
- •9.1. Основные виды финансовых производных
- •9.2. Рыночная стоимость форвардного контракта
- •9.3. Соотношение между рыночной стоимостью форвардного контракта и форвардной ценой базового актива
- •9.4. Форвардные контракты на покупку валюты
- •9.5. Форвардные контракты на процентные ставки
- •9.6. Фьючерсные контракты
- •9.7. Микрохеджирование с помощью фьючерсных контрактов
- •9.8. Макрохеджирование с помощью фьючерсных контрактов
7. Моделирование кредитного риска
7.1. Использование линейной модели вероятности для оценки кредитного риска
Линейная модель вероятности для оценки кредитного риска имеет вид:
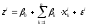 ,
, 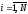 , (1)
, (1)
где
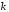 -
вид показателя,
-
вид показателя,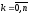 ,
,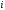 –
номер наблюдения,
–
номер наблюдения,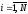 ,
,

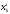 -
значение k-го
финансового показателя для i-го
наблюдения,
-
значение k-го
финансового показателя для i-го
наблюдения,
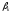 ,
,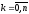 ,
– коэффициенты регрессии,
,
– коэффициенты регрессии,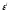 – случайное отклонение.
– случайное отклонение.
Показатели
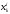 находятся с помощью финансовой отчетности
заемщика, например:
находятся с помощью финансовой отчетности
заемщика, например:
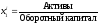 ,
,
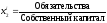 .
.
В модели предполагается, что для потенциального заемщика имеет место равенство, аналогичное равенствам (1), т.е.
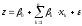 , (2)
, (2)
где
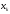 -
(известное) значениеk-го
показателя потенциального заемщика.
-
(известное) значениеk-го
показателя потенциального заемщика.
Заметим, что
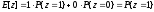 . (3)
. (3)
С другой стороны, как следует из равенства (2):
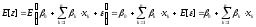 . (4)
. (4)
Из равенств (3) и (4) вытекает, что
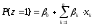 . (5)
. (5)
С
помощью значений
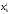 и
и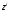 методом наименьших квадратов определяются
оценки
методом наименьших квадратов определяются
оценки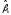 коэффициентов
коэффициентов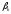 (т.е. решается задача:
(т.е. решается задача: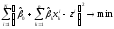 ).
).
Для потенциального заемщика строится прогнозное значение вероятности дефолта по формуле:
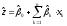 , (6)
, (6)
Основным
недостатком данной модели является то,
что прогнозное значение
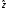 вероятности дефолта может не принадлежать
отрезку
вероятности дефолта может не принадлежать
отрезку .
Модели логит и пробит (которые мы
рассмотрим ниже) позволяют избежать
эту проблему.
.
Модели логит и пробит (которые мы
рассмотрим ниже) позволяют избежать
эту проблему.
(Как
будет показано в следующем параграфе,
в моделях логит и пробит
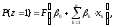 где
где – функция, область значений которой –
интервал , и для потенциального заемщика
прогнозное значение вероятности дефолта
полагается равным
– функция, область значений которой –
интервал , и для потенциального заемщика
прогнозное значение вероятности дефолта
полагается равным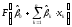 .)
.)
Использование моделей логит и пробит для оценки кредитного риска
В
моделях логит и пробит предполагается,
что для некоторого (ненаблюдаемого)
показателя дефолта
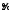 выполнены равенства
выполнены равенства
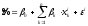 ,
,
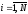 , (7)
, (7)
для известных наблюдений, и равенство
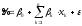 (8)
(8)
для потенциального заемщика.
Причем
без ограничения общности можно считать,
что стандартные отклонения случайных
ошибок
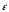 и
и равны 1.
равны 1.
Обозначим
через
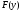 функцию распределения случайных ошибок
функцию распределения случайных ошибок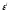 и
и .
В модели логит в качестве
.
В модели логит в качестве![]() выступает функция логистического
распределения:
выступает функция логистического
распределения:
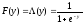 , (9)
, (9)
а в модели пробит – функция стандартного нормального распределения:
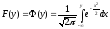 . (10)
. (10)
В
моделях логит и пробит, считается, что
(наблюдаемые) показатели дефолта
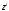 и
и связаны с (ненаблюдаемыми) показателями
связаны с (ненаблюдаемыми) показателями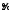 и
и следующим образом:
следующим образом:
 (11)
(11)
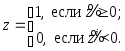 (12)
(12)
Из (8) и (12) следует, что
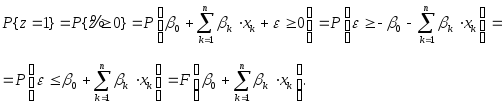 (13)
(13)
Таким образом,
![]() (14)
(14)
Заметим, что из (14) следует, что
![]() (15)
(15)
Отметим,
что для (известных) наблюдений
![]() имеют место равенства, аналогичные (14)
и (15), т.е.
имеют место равенства, аналогичные (14)
и (15), т.е.
![]() (16)
(16)
![]() (17)
(17)
Оценки
![]() коэффициентов
коэффициентов![]() определяются методом максимального
правдоподобия.
определяются методом максимального
правдоподобия.
В силу равенств (16) и (17) функция правдоподобия для моделей логит и пробит имеет вид:
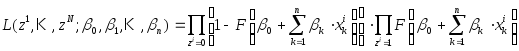 .
(18)
.
(18)
Легко показать, что формулу (18) можно записать в следующем виде:
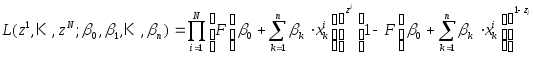 .
(19)
.
(19)
Оценки
![]() получаются в результате максимизации
функции максимального правдоподобия
получаются в результате максимизации
функции максимального правдоподобия![]() по параметрам
по параметрам![]() .
.
Отметим, что максимизация функции правдоподобия эквивалентна максимизации логарифмической функции правдоподобия. (Напомним, что логарифмическая функция правдоподобия равна натуральному логарифму функции правдоподобия.)
Найдем логарифмическую функцию правдоподобия для моделей логит и пробит.
Прологарифмировав формулу (19), получим:
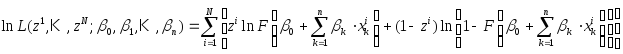 .
(20)
.
(20)
Можно показать, что для моделей логит и пробит логарифмическая функция правдоподобия является вогнутой.
Для
потенциального заемщика прогнозное
значение вероятности дефолта полагается
равным
![]() ,
где
,
где![]() -
(известное) значениеk-го
показателя потенциального заемщика.
-
(известное) значениеk-го
показателя потенциального заемщика.
Дискриминантные модели оценки кредитного риска
Модели, основанные на регрессии.
Наблюдения
делятся на две группы: с дефолтом и без
дефолта. Показателю
![]() i-го
наблюдения (
i-го
наблюдения (![]() )
присваивается некоторое значение для
наблюдений с дефолтом (одно и то же
значение для всех наблюдений с дефолтом)
и некоторое другое значение для наблюдений
без дефолта (одно и то же значение для
всех наблюдений без дефолта).
)
присваивается некоторое значение для
наблюдений с дефолтом (одно и то же
значение для всех наблюдений с дефолтом)
и некоторое другое значение для наблюдений
без дефолта (одно и то же значение для
всех наблюдений без дефолта).
Таким образом,
![]()
Замечание
1. Выбор значений
![]() и
и![]() не играет роли.
не играет роли.
Предполагается, что имеет место уравнение регрессии
![]() ,
, ![]() , (21)
, (21)
где
![]() -
вид показателя,
-
вид показателя,![]() -
значениеk-го
показателя
-
значениеk-го
показателя
![]() i-го
наблюдения,
i-го
наблюдения,
![]() ,
,![]() ,
– коэффициенты регрессии,
,
– коэффициенты регрессии,![]() – случайное отклонение.
– случайное отклонение.
С помощью значений
![]() и
и![]() методом наименьших квадратов определяются
оценки
методом наименьших квадратов определяются
оценки![]() коэффициентов
коэффициентов![]() (т.е. решается задача:
(т.е. решается задача: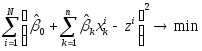 ).
).
Затем
для каждого наблюдения находятся
прогнозные значения
![]() по формуле:
по формуле:
![]() . (22)
. (22)
Обозначим
через
![]() – количество наблюдений с дефолтом,
через
– количество наблюдений с дефолтом,
через![]() – множество индексов
– множество индексов![]() для наблюдений с дефолтом, через
для наблюдений с дефолтом, через![]() – количество наблюдений без дефолта,
через
– количество наблюдений без дефолта,
через![]() – множество индексов
– множество индексов![]() для наблюдений без дефолта.
для наблюдений без дефолта.
В
каждой из двух групп находятся средние
значения
![]() и
и![]() прогнозных значений
прогнозных значений![]() :
:
![]() ,
,
![]() . (23)
. (23)
Для
потенциального заемщика находится
прогнозное значение
![]() показателя
показателя![]() по формуле:
по формуле:
![]() , (24)
, (24)
где
![]() -
(известное) значениеk-го
показателя потенциального заемщика
-
(известное) значениеk-го
показателя потенциального заемщика
Потенциального
заемщика относят к той группе (с дефолтом
или без дефолта), для которой значение
показателя
![]() потенциального
заемщика «ближе» (в некотором смысле)
к среднему значению
потенциального
заемщика «ближе» (в некотором смысле)
к среднему значению![]() группы. Для определения «близости»
группы. Для определения «близости»![]() к
к![]() может использоваться, например, следующая
мера:
может использоваться, например, следующая
мера:
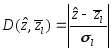 . (25)
. (25)
Здесь
![]() – выборочное стандартное отклонение
показателя
– выборочное стандартное отклонение
показателя![]() для группы
для группы![]() ,
т.е
,
т.е
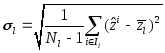 ,
,
![]() . (26)
. (26)
Таким
образом, потенциального заемщика относят
к первой группе (с большим кредитным
риском), если
![]() ,
а ко второй группе (с малым кредитным
риском), если
,
а ко второй группе (с малым кредитным
риском), если![]() .
.
Для
определения, к какому значению
![]() ближе
ближе![]() ,
удобно использовать так называемое
граничное значение
,
удобно использовать так называемое
граничное значение![]() показателя
показателя![]() .
Это значение «равноудалено» от
.
Это значение «равноудалено» от![]() и
и![]() ,
т.е. оно находится из следующего уравнения:
,
т.е. оно находится из следующего уравнения:
![]() . (27)
. (27)
Если,
например, для определения близости
используется формула (25), граничное
значение
![]() находится по формуле:
находится по формуле:
![]() . (28)
. (28)
В
случае, когда
![]() ,
,![]() тогда и только тогда, когда
тогда и только тогда, когда![]() ,
а
,
а![]() тогда и только тогда, когда
тогда и только тогда, когда![]() ,
Следовательно, в этом случае потенциального
заемщика относят к первой группе (с
большим кредитным риском), если
,
Следовательно, в этом случае потенциального
заемщика относят к первой группе (с
большим кредитным риском), если![]() ,
а ко второй группе (с малым кредитным
риском), если
,
а ко второй группе (с малым кредитным
риском), если![]() .
.
В
случае, когда
![]() ,
,![]() тогда и только тогда, когда
тогда и только тогда, когда![]() ,
а
,
а![]() тогда и только тогда, когда
тогда и только тогда, когда![]() ,
Следовательно, в этом случае потенциального
заемщика относят к первой группе (с
большим кредитным риском), если
,
Следовательно, в этом случае потенциального
заемщика относят к первой группе (с
большим кредитным риском), если![]() ,
а ко второй группе (с малым кредитным
риском), если
,
а ко второй группе (с малым кредитным
риском), если![]() .
.
Частным
случаем описанной выше дискриминантной
модели является модель Альтмана. В этой
модели прогнозное значение
![]() для потенциального заемщика находится
по формуле:
для потенциального заемщика находится
по формуле:
![]() . (29)
. (29)
Здесь
![]() следующие финансовые показатели
потенциального заемщика.
следующие финансовые показатели
потенциального заемщика.
![]() -
отношение оборотного капитала к активам
(оборотный капитал – это разница между
краткосрочными активами и краткосрочными
обязательствами);
-
отношение оборотного капитала к активам
(оборотный капитал – это разница между
краткосрочными активами и краткосрочными
обязательствами);
![]() -
отношение нераспределенной прибыли к
активам (нераспределенная прибыль –
это прибыль до выплаты дивидендов);
-
отношение нераспределенной прибыли к
активам (нераспределенная прибыль –
это прибыль до выплаты дивидендов);
![]() -
отношение прибыли до выплаты налогов
и процентов к активам;
-
отношение прибыли до выплаты налогов
и процентов к активам;
![]() -
отношение рыночной стоимости собственного
капитала учетной стоимости долгосрочных
обязательств;
-
отношение рыночной стоимости собственного
капитала учетной стоимости долгосрочных
обязательств;
![]() -
отношение выручки к активам.
-
отношение выручки к активам.
Граничное
значение
![]() в модели Альтмана равно 1,81. Если
прогнозное значение
в модели Альтмана равно 1,81. Если
прогнозное значение![]() для
потенциального заемщика меньше 1,81, то
потенциального заемщика относят к
группе с высоким кредитным риском.
для
потенциального заемщика меньше 1,81, то
потенциального заемщика относят к
группе с высоким кредитным риском.
Множественный дискриминантный анализ
На основании данных о выполнении заемщиками взятых на себя обязательств по выплате займов наблюдения делят на несколько групп.
Обозначим
через
![]() число групп наблюдений, через
число групп наблюдений, через![]() и
и![]() – соответственно, количество наблюдений
и множество индексов в группе
– соответственно, количество наблюдений
и множество индексов в группе![]() .
.
Для
каждой группы
![]() находятся средние значения показателей
находятся средние значения показателей![]() ,
,![]() :
:
![]() . (30)
. (30)
Вектор
![]() называется центроидом группы
называется центроидом группы![]() .
.
Потенциального
заемщика с финансовыми показателями
![]() относят к той группе, к центороиду
которой «ближе» всего вектор
относят к той группе, к центороиду
которой «ближе» всего вектор![]() финансовых
показателей потенциального заемщика.
финансовых
показателей потенциального заемщика.





![]()
Для
определения «близости» вектора
![]() к центроиду
к центроиду![]() может, например, использоваться следующая
мера:
может, например, использоваться следующая
мера:
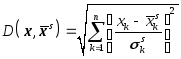 . (31)
. (31)
Здесь
![]() – выборочное стандартное отклонение
параметра
– выборочное стандартное отклонение
параметра![]() в группе
в группе![]() ,
т.е.
,
т.е.
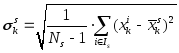 . (32)
. (32)
Итак,
потенциального заемщика относят к той
группе, для которой
![]() минимально.
минимально.
Временная структура кредитного риска
Качество облигаций определяется кредитным риском. Чем выше кредитный риск, тем хуже качество облигаций, и тем выше должна быть доходность облигаций.
Пусть
на рынке имеется бескупонная облигация
с номинальной стоимостью
![]() денежных единиц. Предположим, что номинал
облигации либо выплачивается полностью
в момент погашения, либо не выплачивается
никогда. Обозначим через
денежных единиц. Предположим, что номинал
облигации либо выплачивается полностью
в момент погашения, либо не выплачивается
никогда. Обозначим через![]() вероятность
выплаты номинала. Тогда
вероятность
выплаты номинала. Тогда![]() – это вероятность дефолта.
– это вероятность дефолта.

![]()
![]()
![]() 0
0
Размер
ожидаемого платежа в момент погашения
облигации равен
![]() .
.
Пусть
цена облигации в текущий момент времени
равна
![]() .
Обозначим через
.
Обозначим через![]() эффективную доходность. (Эффективная
доходность
эффективную доходность. (Эффективная
доходность![]() находится из следующего уравнения:
находится из следующего уравнения:![]() .
Следовательно,
.
Следовательно,![]() .)
В расчете на одну денежную единицу,
вложенную в облигации данного вида,
обещанный платеж составит
.)
В расчете на одну денежную единицу,
вложенную в облигации данного вида,
обещанный платеж составит![]() денежный единиц, а ожидаемый платеж –
денежный единиц, а ожидаемый платеж –![]() д.е.
д.е.
Пусть
на рынке также имеются безрисковые
бескупонные облигации с номинальной
стоимостью
![]() ,
срок погашения которых совпадает со
сроком погашения рассмотренных выше
облигаций. (Напомним, что безрисковые
облигации – это облигации, вероятность
дефолта платежей которых равна нулю.)
Для таких облигаций ожидаемый платеж
в момент погашения совпадает с номиналом
,
срок погашения которых совпадает со
сроком погашения рассмотренных выше
облигаций. (Напомним, что безрисковые
облигации – это облигации, вероятность
дефолта платежей которых равна нулю.)
Для таких облигаций ожидаемый платеж
в момент погашения совпадает с номиналом![]() .
.
Пусть
![]() – цена безрисковой облигации в текущий
момент времени. Обозначим, через
– цена безрисковой облигации в текущий
момент времени. Обозначим, через![]() эффективную доходность безрисковых
облигаций. (Эффективная доходность
эффективную доходность безрисковых
облигаций. (Эффективная доходность![]() находится из следующего уравнения:
находится из следующего уравнения:![]() .
Следовательно,
.
Следовательно,![]() .)
.)
Определим
вероятность дефолта
![]() с помощью доходностей
с помощью доходностей![]() и
и![]() .
Для простоты предположим, что инвесторы
нейтральны по отношению к риску, т.е.
для них имеет значение только размер
ожидаемого платежа. В этом случае должно
выполняться равенство:
.
Для простоты предположим, что инвесторы
нейтральны по отношению к риску, т.е.
для них имеет значение только размер
ожидаемого платежа. В этом случае должно
выполняться равенство:
![]() . (33)
. (33)
Действительно,
если
![]() ,
то нейтральные к риску инвесторы будут
избавляться от безрисковых облигаций
и покупать рискованные облигации, что
приведет к снижению цены на безрисковые
облигации и увеличению цены на рискованные
облигации, и, следовательно, доходность
безрисковых облигаций увеличится, а
рискованных облигаций – уменьшится. В
случае, если
,
то нейтральные к риску инвесторы будут
избавляться от безрисковых облигаций
и покупать рискованные облигации, что
приведет к снижению цены на безрисковые
облигации и увеличению цены на рискованные
облигации, и, следовательно, доходность
безрисковых облигаций увеличится, а
рискованных облигаций – уменьшится. В
случае, если![]() ,
будет наблюдаться обратная картина.
Поэтому, в конечном счете, доходности
,
будет наблюдаться обратная картина.
Поэтому, в конечном счете, доходности![]() и
и![]() примут значения, для которых справедливо
равенство (33).
примут значения, для которых справедливо
равенство (33).
Из равенства (33) вытекает, что
![]() . (34)
. (34)
Пример
1.
Доходность рискованной облигации равна
![]() ,
а вероятность безрисковой облигации –
,
а вероятность безрисковой облигации –![]() .
Требуется определить вероятность
дефолта для рискованной облигации
(считая, что инвесторы нейтральны к
риску).
.
Требуется определить вероятность
дефолта для рискованной облигации
(считая, что инвесторы нейтральны к
риску).
Решение.
Итак,
![]() ,
,![]() .
.
![]() .
.
![]() –это
вероятность выплаты номинала рискованной
облигации. Вероятность дефолта равна
–это
вероятность выплаты номинала рискованной
облигации. Вероятность дефолта равна
![]() .
.
Рассмотрим
общий случай. Пусть
![]() – временная структура чистых доходностей
рискованных облигаций, а
– временная структура чистых доходностей
рискованных облигаций, а![]() – временная структура чистых доходностей
безрисковых облигаций. В расчете на
одну денежную единицу, вложенную в
рискованные бескупонные облигации со
сроком погашения в конце периода
– временная структура чистых доходностей
безрисковых облигаций. В расчете на
одну денежную единицу, вложенную в
рискованные бескупонные облигации со
сроком погашения в конце периода![]() ,
обещанный платеж составит
,
обещанный платеж составит![]() д.е., а ожидаемый платеж составит
д.е., а ожидаемый платеж составит![]() д.е., где
д.е., где![]() – вероятность выплаты в конце периода
– вероятность выплаты в конце периода![]() .
В расчете на одну денежную единицу,
вложенную в безрисковые бескупонные
(возможно синтетические) облигации со
сроком погашения в конце периода
.
В расчете на одну денежную единицу,
вложенную в безрисковые бескупонные
(возможно синтетические) облигации со
сроком погашения в конце периода![]() ,
обещанный платеж составит
,
обещанный платеж составит![]() д.е. Следовательно, в случае, когда
инвесторы нейтральны к риску, справедливо
равенство:
д.е. Следовательно, в случае, когда
инвесторы нейтральны к риску, справедливо
равенство:
![]() . (35)
. (35)
Отсюда следует, что
![]() . (36)
. (36)
В случае, когда на рынке отсутствуют рискованные бескупонные облигации, формулу (36) можно получить следующим образом.
Пусть
чистые доходности рискованных облигаций
получены с помощью
![]() облигаций с невырожденной матрицей
платежей:
облигаций с невырожденной матрицей
платежей:
![]() ,
,
![]() . (37)
. (37)
Здесь
![]() –k-й
платеж облигации i-го
вида,
–k-й
платеж облигации i-го
вида,
![]() – цена облигацииi-го
вида.
– цена облигацииi-го
вида.
В случае, когда инвесторы нейтральны к риску, должны выполняться следующие равенства:
![]() ,
,
![]() . (38)
. (38)
Равенства
(38) означают, что цена инвестиционной
стратегии, состоящей в покупке и продаже
безрисковых облигаций и выплачивающей
платежи
![]() ,
,![]() ,
должна быть равной цене
,
должна быть равной цене![]() рискованной облигацииi-го
вида.
рискованной облигацииi-го
вида.
Из уравнений (37) и (38) следуют равенства (36). (Действительно, подставив формулы (36) в равенства (38) получим равенства (37).)
Пример 2. Для второго периода чистая доходность рискованных облигаций равна 18%, а чистая доходность безрисковых облигаций – 12%. Требуется найти вероятность дефолта для платежей рискованных облигаций в конце второго периода.
Решение.
Итак,
![]() ,
,![]() .
.
![]() .
.
![]() –это
вероятность выплаты платежей рискованных
облигаций в конце второго периода.
Вероятность дефолта для платежей
рискованных облигаций в конце второго
периода равна
–это
вероятность выплаты платежей рискованных
облигаций в конце второго периода.
Вероятность дефолта для платежей
рискованных облигаций в конце второго
периода равна
![]() .
.
Найдем
условные вероятности выплаты и дефолта
в периоде
![]() при условии, что платежи были выплачены
во всех предшествующих периодах.
(Обозначим такую условную вероятность
через
при условии, что платежи были выплачены
во всех предшествующих периодах.
(Обозначим такую условную вероятность
через![]() ).
В соответствии с определением условной
вероятности, вероятность
).
В соответствии с определением условной
вероятности, вероятность![]() равна отношению вероятности выплаты
платежей в периодах с первого поk-ый
к вероятности выплаты платежей в
периодах с первого по (k-1)-ый.
равна отношению вероятности выплаты
платежей в периодах с первого поk-ый
к вероятности выплаты платежей в
периодах с первого по (k-1)-ый.
Предположим,
что для рискованных облигаций платежи
в каждом периоде могут быть выплачены
только в том случае, когда были выплачены
платежи во всех предшествующих периодах.
Тогда вероятность выплаты платежей в
периодах с первого по k-ый
равна вероятности
![]() выплаты платежа в периоде
выплаты платежа в периоде![]() ,
а вероятность выплаты платежей в периодах
с первого по (k-1)-ый
равна вероятности
,
а вероятность выплаты платежей в периодах
с первого по (k-1)-ый
равна вероятности
![]() выплаты платежа в периоде
выплаты платежа в периоде![]() .
Следовательно, в этом случае
.
Следовательно, в этом случае
![]() . (39)
. (39)
Пример 3. Чистая доходность рискованных облигаций равна 15,8% для первого периода и 18% для второго периода. Чистая доходность безрисковых облигаций равна 10% для первого периода и 12% для второго периода. Требуется найти вероятность дефолта для платежа во втором периоде при условии, что платеж в первом периоде был выплачен.
Решение.
Итак,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() –это
вероятность выплаты платежа в конце
второго периода при условии, что платеж
в первом периоде был выплачен. Вероятность
дефолта для платежа во втором периоде
при условии, что платеж в первом периоде
был выплачен, равна
–это
вероятность выплаты платежа в конце
второго периода при условии, что платеж
в первом периоде был выплачен. Вероятность
дефолта для платежа во втором периоде
при условии, что платеж в первом периоде
был выплачен, равна
![]() .
.
Условная
вероятность
![]() может быть также вычислена с помощью
форвардных доходностей. Подставив
формулу (36) в (37), получим:
может быть также вычислена с помощью
форвардных доходностей. Подставив
формулу (36) в (37), получим:
![]() . (40)
. (40)
Поскольку
![]() и
и![]() ,
из (28) следует, что
,
из (28) следует, что
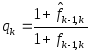 . (41)
. (41)
