
Информатика_Методы
.pdf
21.01.2013
известно k-е приближение к истинному
решению ( x1(k ) , x2(k ) , , xn(k ) ).
Тогда точное решение ( x1 , x2 можно представить в виде
( x1(k ) x1(k ) , x2(k ) x2(k ) , , xn(k )
,, xn )
xn(k ) ),
где x1(k ) , x2(k ) , , xn(k ) - поправки
(погрешности истинного решения).
Подставим точное решение в исходную систему уравнений
101
101

21.01.2013
|
( k ) |
(k ) |
( k ) |
( k ) |
( k ) |
( k ) |
|
f1 ( x1 |
x1 |
, x2 |
x2 |
, , xn |
xn |
) 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
( k ) |
(k ) |
( k ) |
( k ) |
( k ) |
( k ) |
) 0, |
fn |
( x1 |
x1 |
, x2 |
x2 |
, , xn |
xn |
|
Неизвестными в этой системе |
|
||||||
являются поправки x1(k ) , x2(k ) , , xn(k )
Предполагая, что функции f i непрерывно дифференцируемы в некоторой выпуклой области, содержащей xi и xi( k ) , разложим левые части уравнений в степенные ряды, ограничиваясь линейными членами
102
102

21.01.2013
|
|
( k ) |
( k ) |
( k ) |
( k ) |
|
|
|
( k ) |
|
( k ) |
|
|
|
|
f1 ( x1 |
x1 |
, , xn |
xn |
) f1 ( x1 |
, , xn |
) |
|
||||||||
|
|
|
|
|
|
( k ) f1 |
|
( k ) |
|
f1 |
|
|
|||
|
|
|
|
|
x1 |
|
|
xn |
|
|
|
|
0, |
||
|
|
|
|
x1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
xn |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
f |
n |
( x( k ) x( k ) , , x( k ) x( k ) ) f |
n |
( x( k ) , , x( k ) ) |
|||||||||||
|
1 |
1 |
n |
n |
|
|
1 |
|
|
n |
|
|
|
||
|
|
|
|
|
x1( k ) fn |
xn( k ) |
|
fn |
0. |
||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
x1 |
|
|
|
xn |
||||
Приведем получившуюся линейную систему к традиционному виду
103
103

21.01.2013
|
f1 |
x( k ) |
f1 |
x( k ) f |
( x(k ) , , x( k ) ), |
|||
|
|
|
|
|||||
x |
1 |
x |
|
n |
1 |
1 |
n |
|
|
|
|
|
|
|
|||
|
1 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
f |
n |
|
f |
n |
|
|
|
|
x1( k ) |
|
xn( k ) fn ( x1(k ) , , xn( k ) ). |
|||
|
|
x |
|
||||
x |
|
n |
|
||||
|
|
1 |
|
|
|
|
|
Такую систему линейных уравнений можно решить прямым методом, например, методом исключения Гаусса
иполучить значения поправок
x1(k ) , x2(k ) , , xn(k ) .
104
104

21.01.2013
Вычисленные поправки позволяют перейти к следующему k+1 приближению решения
x(k 1) |
x(k ) x(k ) , |
i 1, 2, ..., n. |
|
i |
i |
i |
|
Оно не совпадет с точным решением (поправки вычислены приближенно), но приблизится к нему. Потребуется несколько раз вычислять поправки и переходить к следующему приближению. Если на очередной итерации все поправки становятся достаточно малыми (меньше заданной
погрешности ε), то расчет прекращается.
105
105
21.01.2013
xi xi |
xi , |
i 1, |
..., n |
|
|
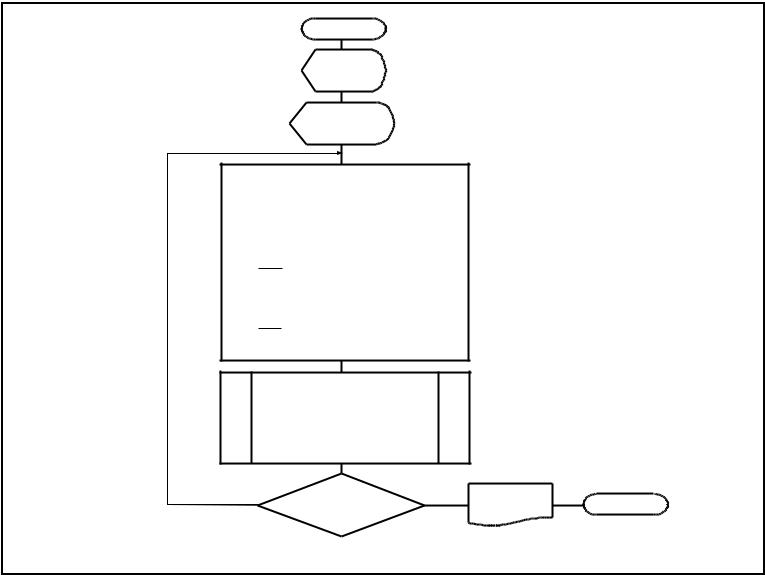
начало
ввод n,
ввод
xi , i=1,…,n
Формирование матрицы A[n,n] и вектора B[n]:
f1
x1f2
A x1
fnx1
f1 |
|
f1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
x2 |
xn |
|
|
f |
|
||||
f2 |
|
f2 |
|
|
|
1 |
|
||
|
|
|
f2 |
||||||
|
|
|
|
|
, B |
|
|
||
x |
|
x |
|
||||||
2 |
|
n |
|
|
|
||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||
fn |
|
fn |
|
fn |
|||||
|
|
|
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
||
2 |
|
n |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
Решение системы линейных уравнений относительно поправокxi методом исключения
неизвестных Гаусса
нет |
| x |
i |
| , |
да |
xi , |
конец |
|
|
|
|
i=1,…, n |
||
|
i 1,..., n |
|
|
|||
|
|
|
|
|||
Алгоритм метода Ньютона |
106 |
|
106

21.01.2013
ПРИБЛИЖЕННОЕ
ВЫЧИСЛЕНИЕ
ИНТЕГРАЛОВ
107
107

21.01.2013
В классической математике определенный интеграл вычисляется через первообразные по формуле Ньютона-Лейбница
b
f ( x)dx F (b) F (a)
a
Эта формула не удобна для вычислений на компьютере, поскольку процедура получения первообразной F(x) может быть сложной.
108
108

21.01.2013
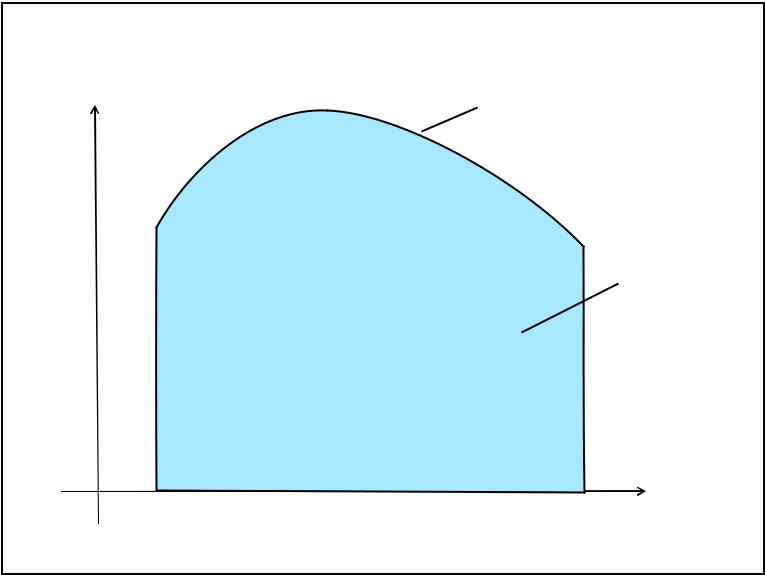
В практических вычислениях прибегают к приближенным методам, основанным на геометрическом смысле интеграла.
С геометрической точки зрения значение определенного интеграла
b
I f ( x)dx
a
есть площадь фигуры, ограниченная кривой f (x), прямыми x = a, x = b и осью абсцисс.
109
109
21.01.2013
Площадь S криволинейной трапеции |
|||
y |
|
f (x) |
|
|
|
|
S = I |
0 |
a |
b |
x |
|
|
|
110 |
110
