
- •Программная реализация численных методов и анализ результатов численного эксперимента
- •Методические указания
- •К курсовым работам по дисциплинам
- •«Информатика» и «Языки и технология программирования»
- •Содержание
- •Введение
- •1. Цель и задачи курсовых работ
- •2. Задание на курсовые работы
- •3. Структура пояснительной записки
- •Вычисление второй производной
- •4.1.2. Численное интегрирование функций
- •Метод Эйлера
- •4.1.3. Численное решение нелинейных уравнений
- •Метод бисекций
- •Метод простых итераций
- •Метод Ньютона (касательных)
- •Метод хорд (секущих)
- •4.2. Применение экстраполяции для оценки погрешности
- •Численная фильтрация
- •Метод Эйткена
- •Критерий размытости оценки
- •Визуализация результатов экстраполяции
- •4.3. Разработка программ, реализующих комбинацию численных методов
- •5. Пример курсовой работы
- •Список Литературы
- •Образец оформления бланка задания на курсовую работу
- •Образец оформления титульного листа пояснительной записки
- •Уфимский государственный авиационный технический университет
- •Пояснительная записка
4.3. Разработка программ, реализующих комбинацию численных методов
Вторая курсовая работа заключается в разработке программы, реализующей решение уравнения одним из перечисленных методов в случае, когда в уравнение входит интеграл от известной функции с неизвестным параметром, который должен быть определен при решении уравнения.
Рассмотрим задачу
![]() .
.
При этом параметр z cчитается заданным, а y(z) определяется из решения уравнения. Таким образом, для решения задачи требуется использование одного из методов численного решения нелинейных уравнений и одного из методов численного интегрирования функций.
При разработке программ, реализующих численные методы, необходимо придерживаться общепринятого стиля: подпрограмма, реализующая конкретный метод, должна обладать определенной универсальностью и независимостью от вида функции, к которой применяется численный метод.
Из этого следует, что подпрограмма численного интегрирования в качестве формальных параметров должна содержать пределы интегрирования a,b верхнюю оценку погрешности , имя подынтегральной функции, которая внутри подпрограммы должна иметь вид f(x). Поэтому параметры y и z не включаются в число формальных, а значит, являются внешними. Экстраполяция и оценка погрешности должна быть включена в подпрограмму численного интегрирования. Визуализация результатов экстраполяции должна быть предусмотрена и включаться в определенный момент расчета (как правило, в конце) по желанию пользователя.
Подпрограмма
решения нелинейного уравнения
![]() в качестве формальных параметров должна
содержать границы интервала поиска
A,B,
верхнюю границу погрешности решения
уравнения E,
имя функции
в качестве формальных параметров должна
содержать границы интервала поиска
A,B,
верхнюю границу погрешности решения
уравнения E,
имя функции
![]() ,
имя переменной y,
значение которой является выходным
параметром. В связи с этим, необходима
подпрограмма, вычисляющая значения
этой функции. В нашем случае
,
имя переменной y,
значение которой является выходным
параметром. В связи с этим, необходима
подпрограмма, вычисляющая значения
этой функции. В нашем случае
![]() .
Параметры z
и C
являются
для нее внешними. Из этой функции
производится обращение к подпрограмме
численного интегрирования. Примерная
укрупненная блок-схема программы
изображена на рис. 12.
.
Параметры z
и C
являются
для нее внешними. Из этой функции
производится обращение к подпрограмме
численного интегрирования. Примерная
укрупненная блок-схема программы
изображена на рис. 12.
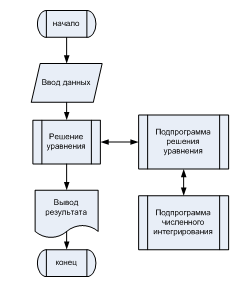
Рис. 12. Блок-схема программы, реализующей комбинацию численных методов
С помощью такой программы можно решить задачу построения зависимости y(z). Для этого необходимо задать последовательность значений zj, j=1,…,M и вычислить соответствующие значения yj=(zj). Результаты вычислений следует представить как в табличном, так и в графическом виде. Примерный графический интерфейс программы прилагается (прил. П3.1).
5. Пример курсовой работы
Содержание
курсовой работы рассмотрим на примере:
“Оценка погрешности и уточнение методом
Ромберга результатов вычисления второй
производной по центрально-симметричной
разностной формуле”. В качестве
дифференцируемой функции выберем
![]() при x=0.5.
при x=0.5.
5.1. Описание метода вычисления второй производной по центрально-симметричной разностной формуле (см. п. 3, формула (5)).
5.2. Программная реализация метода вычисления второй производной по центрально-симметричной разностной формуле (прилагается листинг программы с комментариями).
5.3. Оценка погрешности результата, уточнение результата, визуализация результатов уточнения.
5.3.1. В результате выполнения программы реализующей вычисление второй производной функции , были получены следующие результаты zn (прил. П3.2).
При этом на каждом шаге происходит увеличение числа разбиений в 2 раза, т.е. Q=2.
5.3.2. Далее определяется разница результата на следующем и предыдущем шаге (прил. П3.3)
![]()
5.3.3. Вычисляем отношения (прил. П3.3.1)

5.3.4. Потом экстраполируем полученный результат (прил. П3.3.2):
Для метода Ромберга определяем порядок точности метода из приближенного равенства QkKn. Проводим экстраполяцию по формуле Ричардсона
![]() ;
;
Для метода Эйткена для экстраполяции используется полученные значения Kn
![]() .
.
Далее
шаги 2,3 повторяются, до тех пор, пока
![]() .
Нарушение этого равенства свидетельствует
о том, что дальнейшее уточнение результата
невозможно.
.
Нарушение этого равенства свидетельствует
о том, что дальнейшее уточнение результата
невозможно.
5.3.5. Строятся графики в логарифмической шкале:
a)
Строится график полученных результатов
в сравнении с точным результатом. По
оси абсцисс откладывается lgn,
по оси ординат
значения
![]() ,
,
![]() ,
….
,
….
Полученные результаты прилагаются (прил. П3.3.3).
б)
Строится график полученных результатов
в сравнение с “эталонным” значением.
В качестве эталона выбирается наиболее
точный результат z,
полученный при проведении последней
экстраполяции. По оси абсцисс откладывается
lgn,
по оси ординат
– значения
![]() ,
,
![]() ,
,
![]() ,…
,…
Полученные результаты прилагаются (прил. П3.3.4).
в)
Оценка результатов производится по
правилу Рунге
![]() ,
,
![]() ,…
Строится график полученных результатов,
,…
Строится график полученных результатов,
По
оси абсцисс откладывается lgn,
по оси ординат
значения
-lg![]() ,
-lg
,
-lg![]() ,
…
,
…
Полученные результаты прилагаются (прил. П3.3.5).
