
- •Программная реализация численных методов и анализ результатов численного эксперимента
- •Методические указания
- •К курсовым работам по дисциплинам
- •«Информатика» и «Языки и технология программирования»
- •Содержание
- •Введение
- •1. Цель и задачи курсовых работ
- •2. Задание на курсовые работы
- •3. Структура пояснительной записки
- •Вычисление второй производной
- •4.1.2. Численное интегрирование функций
- •Метод Эйлера
- •4.1.3. Численное решение нелинейных уравнений
- •Метод бисекций
- •Метод простых итераций
- •Метод Ньютона (касательных)
- •Метод хорд (секущих)
- •4.2. Применение экстраполяции для оценки погрешности
- •Численная фильтрация
- •Метод Эйткена
- •Критерий размытости оценки
- •Визуализация результатов экстраполяции
- •4.3. Разработка программ, реализующих комбинацию численных методов
- •5. Пример курсовой работы
- •Список Литературы
- •Образец оформления бланка задания на курсовую работу
- •Образец оформления титульного листа пояснительной записки
- •Уфимский государственный авиационный технический университет
- •Пояснительная записка
4.1.2. Численное интегрирование функций
Пусть необходимо вычислить определенный интеграл от некоторой непрерывной функции f(x)
![]() . (6)
. (6)
Численное значение интеграла равно площади, заключенной между кривой y= f(x), осью x и вертикальными прямыми x=a и x=b (рис. 2).
Разобьем
отрезок интегрирования на n
частей. Введем в рассмотрение
последовательность узловых точек
xj[a,b],
xj=a+jh,
j=0,...,n.
Величина
![]() называется шагом разбиения. Обозначим
fj=f(xj).
называется шагом разбиения. Обозначим
fj=f(xj).
С помощью такого разбиения площадь криволинейной фигуры удается вычислить намного точнее и проще, чем без разбиения (см. рис. 2).

Рис. 2. Численное интегрирование
Таким образом, интеграл представляется суммой интегралов
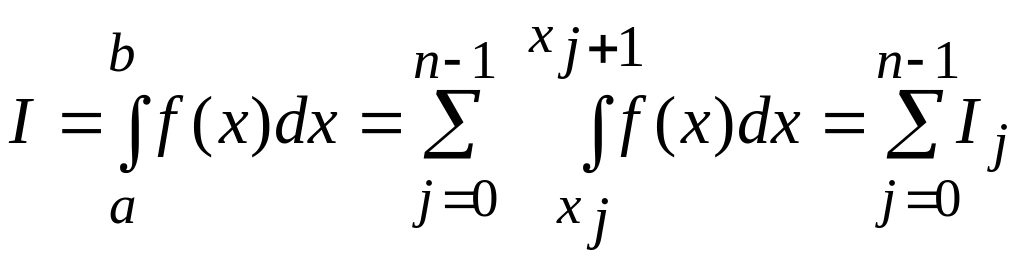 . (7)
. (7)
Метод левых прямоугольников
Вместо площади криволинейной фигуры вычисляется площадь прямоугольника, высота которого равна значению функции f(x) в крайней левой точке (рис. 3, а)
![]() . (8)
. (8)
![]() . (9)
. (9)
а |
б |
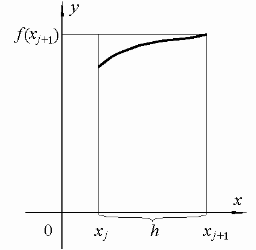
Рис. 3. Методы левых (а) и правых (б) прямоугольников
Метод правых прямоугольников
Вместо площади криволинейной фигуры вычисляется площадь прямоугольника, высота которого равна значению функции f(x) в крайней правой точке (рис. 3, б)
![]() . (10)
. (10)
![]() . (11)
. (11)
Метод средних прямоугольников
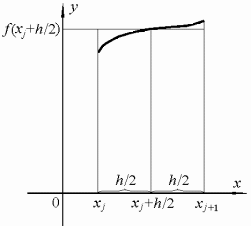
Для вычисления интеграла можно использовать значение функции в середине отрезка (рис. 4, а)
![]() . (12)
. (12)
![]() . (13)
. (13)
Метод трапеций
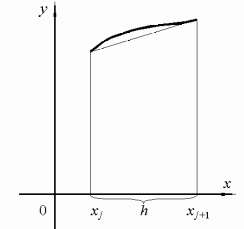
Теперь рассмотрим численное интегрирование фигуры, полученной путем соединения отрезком прямой двух точек на графике функции. Полученная фигура является трапецией (рис. 4, б). Тогда интеграл приближенно равен ее площади
![]() , (14)
, (14)
![]()
 (15)
(15)
а |
б |
Рис. 4. Методы средних прямоугольников (а) и трапеций (б)
Численное решение задачи Коши для обыкновенных дифференциальных уравнений
Постановка задачи
Рассмотрим сначала следующую задачу. Пусть задано обыкновенное дифференциальное уравнение первого порядка
![]() (16)
(16)
и начальное условие
![]() . (17)
. (17)
Такая задача называется задачей Коши для обыкновенного дифференциального уравнения.
Известно, что решение обыкновенного дифференциального уравнения первого порядка для непрерывной функции f(x) графически представляется в виде однопараметрического семейства кривых (см. например, рис. 5, а). Задание начального значения позволяет выбрать из этого семейства одну кривую, которая является решением задачи Коши.
|
|
Рис. 5. Решение задачи Коши для обыкновенного дифференциального уравнения
Для численного решения задачи введем сетку xj, j=0,...,n, x0=a. Верхняя граница xn=b выбирается исходя из условий практического приложения результатов расчета. В случае равномерного разбиения с шагом h узловые точки определяются следующим образом: xj=a+jh. Обозначим yj=y(xj). Тогда
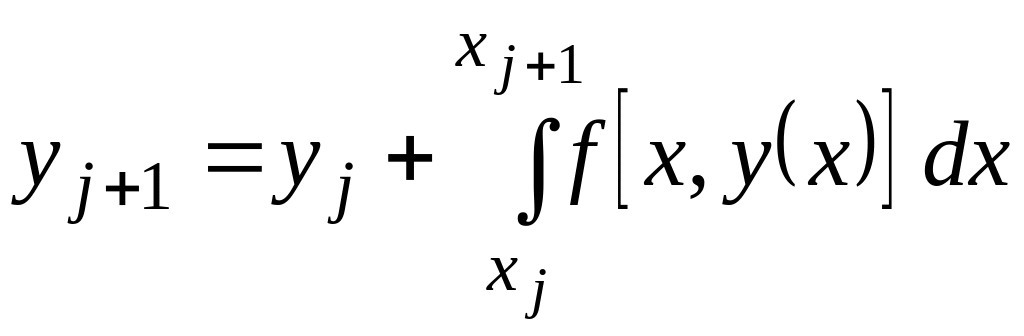 . (18)
. (18)
Однако в отличие от задачи интегрирования функций под знак интеграла входит неизвестная зависимость y(x). Поэтому интегрирование не может быть осуществлено точно. Но существуют способы сделать это приближенно.

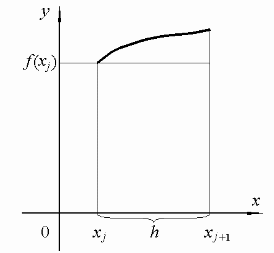
 а
а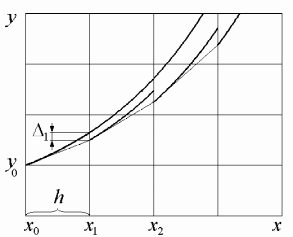 б
б