37

Змістовий модуль № 1 «ХВИЛЬОВА ОПТИКА»

Лабораторна робота № 1.1

ВИЗНАЧЕННЯ ГОЛОВНОЇ ФОКУСНОЇ ВІДСТАНІ

ЗБИРАЛЬНИХ І РОЗСІЮВАЛЬНИХ ЛІНЗ

Мета роботи: ознайомлення із засобами експериментального вивчення оптичних систем.

Прилади і матеріали:

1. оптична лава з повзунками для розміщення освітлювача, екрана і лінз (або їх систем);

2. набір збиральних та розсіювальних тонких лінз;

3. освітлювач із закріпленим перед ним предметом, зображення якого утворюється на екрані;

4. екран;

5. лінійка.

Теоретичні відомості та опис приладів

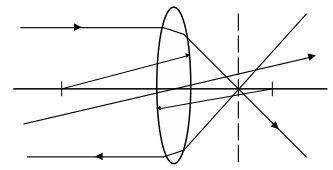
Лінза являє собою оптично прозоре тіло, обмежене двома сферичними або іншої форми заломлюючими поверхнями. Точки О₁, О₂ – центри кривизни сферичних поверхонь лінзи з радіусами R₁, R₂. Пряма лінія, що проходить через центри кривизни О₁ і О₂, називається головною оптичною віссю лінзи (рис. 1).

2 F 3

R₁

O₁ C₂ C₁ f O₂

O

1 R₂

F

Рис.1. Елементи лінзи

Лінзи бувають тонкими і товстими. Лінзу називають тонкою, якщо її товщиною можна знехтувати порівняно з радіусами кривизни поверхонь.

Точка О, що лежить між вершинами сферичних поверхонь С₁, С₂, називається центром лінзи. Будь-яка пряма лінія, проведена через центр лінзи, називається оптичною віссю лінзи.

Точка f, в якій збираються після заломлення промені, що падають на лінзу паралельно головній оптичній осі, називається головним фокусом (переднім або заднім) лінзи. Площини, що проходять через фокуси лінзи і перпендикулярні до головної оптичної осі, називаються фокальними (FF). У фокальній площині розміщені головні та додаткові фокуси лінзи .

Головна фокусна відстань тонкої лінзи f пов’язана з її геометричними (радіуси кривизни сферичних поверхонь R₁, R₂, які обмежують лінзу) і оптичними (абсолютні показники заломлення речовини лінзи n₂ і оточуючого середовища n₁) параметрами таким співвідношенням:

(1)

де - відносний показник заломлення. Величина 1/f=D називається оптичною силою лінзи. Одиницею оптичної сили є діоптрія (дптр). Діоптрія – це оптична сила лінзи у повітрі, фокусна відстань якої дорівнює 1м. Радіус кривизни поверхні вважається додатним, якщо центр кривизни знаходиться праворуч від поверхні, і від’ємним – якщо ліворуч.

Тонкі лінзи називають додатними, якщо f > 0, і від’ємними, якщо f < 0. Додатні лінзи збирають світлові промені і називаються збиральними, а від’ємні розсіюють промені і називаються розсіювальними.

Важливою властивістю лінз є їх здатність давати зображення. При цьому для тонких лінз головна фокусна відстань f і оптична сила D пов’язані з відстанями від лінзи до предмета a і до зображення b співвідношенням:

(2)

У цій формулі знак "+" відповідає збиральній, а знак "−" – розсіювальній лінзам.

Для побудови зображень в тонкій лінзі використовують характерні промені:

1. промінь 1, що проходить через оптичний центр тонкої лінзи, напряму поширення не змінює (не заломлюється);

2. промінь 2, що падає паралельно головній оптичній осі лінзи, після заломлення перетинає цю вісь у фокусі лінзи f ;

3. промінь 3, що падає на лінзу і проходить через її фокус, виходить з лінзи паралельно її головній оптичній осі.

Для побудови зображень точки в тонкій лінзі достатньо використати два промені з трьох.

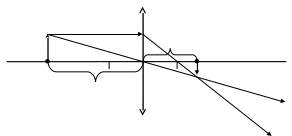
Побудуємо зображення предмета АВ у тонкій збиральній лінзи (рис.2). Для цього треба знайти зображення кожної його точки. Але достатньо знайти точку перетину В’ будь-яких двох променів з трьох (1,2,3), що виходять із точки В предмета АВ. Візьмемо промені 1 і 2, що проходять через оптичний центр О і паралельно головній оптичній осі. За лінзою ці промені перетинаються в точці В’. З точки В’ встановимо перпендикуляр до головної оптичної осі та знайдемо точку перетину А’. Якщо в точці А’ поставити екран, то на ньому, як видно з рис. 2, одержується дійсне, обернене і зменшене зображення предмета А’В’.

B 2

h 1 b A'

A f f h'

a B' 1'

2'

Рис. 2. Побудова зображення предмета у збиральній лінзі

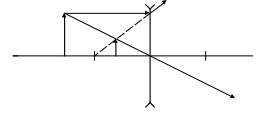
Побудова зображення у розсіювальній лінзі наведена на рис. 3. Промінь 1 проходить через оптичний центр О, не заломлюючись, а промінь 2 своїм уявним продовженням (пунктир) минає через передній фокус f . Зображення В’ точки В одержується на перетині променя 1 і уявного продовження променя 2. З точки В’ встановимо перпендикуляр до головної оптичної осі та знайдемо точку перетину А’. У підсумку одержується, як видно з рис. 3, уявне пряме зображення предмета А’В’.

B 2 2'

1 B'

A f A' 1' f

Рис. 3. Побудова зображення предмета у розсіювальній лінзі

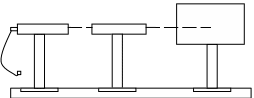
Для дослідного визначення головних фокусних відстаней тонких лінз (або їх систем) використовують оптичну лаву 1 (рис.4). На лаві закріплюється повзунок з освітлювачем і світним предметом 2 (освітлена електричною лампою діафрагма з отвором, який обмежує сітку-предмет); повзунок з досліджуваною лінзою 3 та повзунок з екраном 4. Лінзи і предмет установлюють так, щоб центри їх були розташовані вздовж однієї осьової лінії. Правильність установки перевіряють переміщенням лінзи вздовж оптичної лави. При такому переміщенні центр зображення на екрані не повинен зміщуватися.

Для характеристики зображення, утвореного лінзою, крім його положення потрібно знати і розмір зображення. За означенням поперечного збільшення та з рис. 2 можна записати, що

.

З цього виразу

2 3 4

1

Рис. 4. Схема експериментальної установки

Скориставшись формулою (2), знайдемо зв’язок розмірів предмета та його зображення з фокусною відстанню лінзи:

(3)

де h і h' – відповідно розміри предмета та його зображення на екрані.

Визначення фокусної відстані лінзи за формулами (2) і (3) потребує вимірювання кількох величин, що впливає на значення похибки результату цього непрямого вимірювання.

Розсіювальні лінзи не дають дійсного зображення предмета на екрані. У цьому випадку для визначення фокусної відстані розсіювальної лінзи створюють збиральну центровану систему із розсіювальної і збиральної лінз. При цьому на екрані дістають дійсне зображення предмета. Оптична сила такої системи лінз визначається формулою

(4)

де f_c – фокусна відстань системи лінз; f₁ і f₂ – фокусні відстані лінз, що входять в систему; d – відстань між головними площинами лінз, з яких складається система. Якщо лінзи досить тонкі і торкаються одна одної, то d можна вважати таким, що дорівнює нулю. Тоді оптична сила системи лінз дорівнює сумі оптичних сил лінз, які входять до цієї системи.

Можна зробити й інакше. Підбирають допоміжну збиральну лінзу з оптичною силою, більшою ніж у розсіювальної лінзи. За допомогою цієї збиральної лінзи дістають на екрані дійсне зображення предмета (рис. 5). Потім між екраном і збиральною лінзою поміщають розсіювальну лінзу на відстані d від екрана. При цьому різке зображення зникає. Переміщуючи екран на відстань від розсіювальної лінзи, знову дістають різке зображення предмета. Оскільки роль предмета для розсіювальної лінзи відіграє зображення, утворене за допомогою збиральної лінзи, то для розсіювальної лінзи

(5)

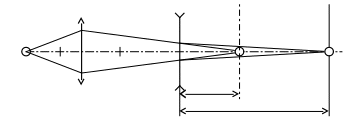E' E

S F₁ F₂

а

b

Рис. 5. Визначення фокусної відстані розсіювальної лінзи