3.2. Арифметичні операції зі збіжними послідовностями

Теорема 9.

1) Якщо , – нескінченно малі послідовності, то – нескінченно мала послідовність (сума і різниця нескінченно малих є нескінченно мала).

2) Якщо – нескінченно мала, – обмежена послідовність, то – нескінченно мала (добуток нескінченно малої на обмежену є нескінченно мала).

3) Якщо – нескінченно велика, то – нескінченно мала.

4) Якщо – нескінченно мала, , то – нескінченно велика.

Доведення.

1. ; .

Позначимо , тоді

.

2. – обмежена послідовність , .

Тоді маємо .

Теорема 10. Якщо є дві збіжні послідовності і , , то:

1. ;

2. ;

3. при .

Доведення.

За теоремою 8 маємо: , , де – нескінченно малі.

1. . За теоремою 9 – нескінченно мала, значить за теоремою 8:

.

2. . За теоремою 9 – нескінченно мала, значить за теоремою 8:

.

3.

Очевидно, вираз в квадратних дужках є нескінченно мала. Доведемо, що – обмежена. . Оскільки , то для числа . Тому при – обмежена. За теоремою 9 – нескінченно мала, за теоремою 8 .

3.3. Монотонні послідовності. Теорема Веєрштраса

Означення. Послідовність називається неспадною (незростаючою), якщо має місце нерівність: . Незростаючі і неспадні (спадні і зростаючі) послідовності називаються монотонними.

Теорема Веєрштраса.

1. Будь-яка неспадна обмежена зверху послідовність збігається.

2. Будь-яка незростаюча обмежена знизу послідовність збігається.

Доведення.

Нехай – неспадна послідовність, обмежена зверху: , ( – верхня межа). За теоремою про точну верхню межу обмеженої зверху множини, існує скінченна точна верхня межа множини . Нехай .

Доведемо, що . Оскільки , то число не є верхньою межею . Оскільки послідовність неспадна, то при . При це еквівалентно . За означенням .

Аналогічно доводиться друга частина теореми.

3.4. Число

Розглянемо послідовність , .

Доведемо, що ця послідовність зростаюча і обмежена зверху. Скористаємося формулою бінома Ньютона:

Розглянемо ;

Порівнюючи доданки і , одержимо:

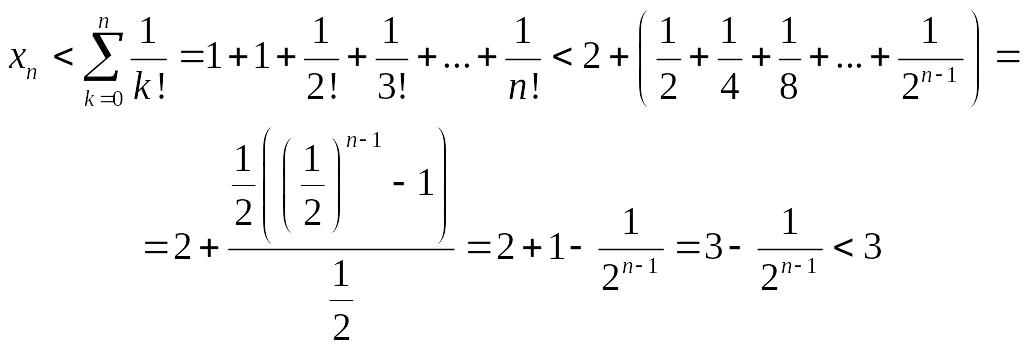
Отже, , – обмежена зверху послідовність. За теоремою Веєрштраса вона має границю, яку позначають .

.

– ірраціональне число.

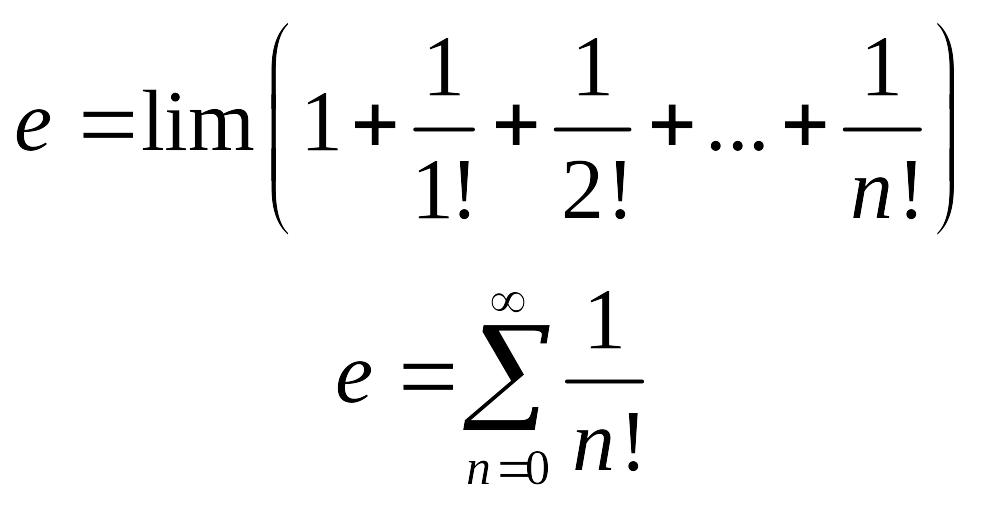
3.5. Підпослідовності

Означення. Послідовність , яка складена з членів послідовності і в якій порядок слідування її членів співпадає з їх порядком слідування в вихідній послідовності , називається підпослідовністю цієї послідовності.

– вихідна послідовність;

– послідовність з натуральних чисел;

– підпослідовність.

Теорема 1. Якщо збіжна послідовність, то будь-яка її підпослідовність збігається до тієї ж границі.

Доведення.

Нехай .

Це означає, що .

Нехай – підпослідовність послідовності . Оскільки нескінченна, то , а значить за принципом Архімеда . Отже, .

Теорема 2. Якщо дві підпослідовності з , об’єднання яких дає , збігаються до однієї і тієї ж границі , то і вся послідовність збігається до .

Теорема 3. (Лема Больцано-Веєрштраса). З будь-якої обмеженої послідовності можна вилучити збіжну підпослідовність.

Доведення.

Нехай – обмежена . Нехай = . Так як – обмежена, то за теоремою про граничну точку множина має хоча б одну граничну точку. Нехай – гранична точка . Тоді в околі знайдеться хоча б один елемент (з послідовності ) відмінний від . Позначимо його через . Продовжуючи процес, одержимо підпослідовність послідовності , причому або . Звідси за теоремою про двох міліціонерів маємо, що .