
- •Передмова
- •Логічна символіка
- •1. Елементи теорії множин
- •1.1. Операції над множинами
- •1.2. Поняття відображення або функції
- •1.3. Еквівалентні множини. Потужність множини
- •1.3.1. Властивості еквівалентних множин
- •1.4. Зліченні множини
- •1.5. Метод математичної індукції
- •1.5.1. Аксіоми натуральних чисел
- •1.5.2. Метод математичної індукції
- •1.6. Біноміальні коефіцієнти. Біном Ньютона
- •2. Аксіоматика дійсних чисел
- •1. Операція додавання.
- •2. Операція множення.
- •3. Зв’язок операцій додавання і множення.
- •4. Аксіома упорядкованості.
- •5. Аксіома неперервності.
- •2.1. Наслідки із аксіом
- •2.1.1. Властивості операцій додавання і множення
- •2.5. Обмежені і необмежені множини. Верхня і нижня межі
- •2.6. Точна верхня і точна нижня межі множини
- •2.7. Принцип Архімеда
- •2.8. Принцип вкладених відрізків
- •2.9. Незліченність відрізка
- •2.10. Теорема про скінченне покриття
- •2.11. Теорема про граничну точку
- •3. Границя числової послідовності
- •3.1. Теореми про границі
- •3.2. Арифметичні операції зі збіжними послідовностями
- •3.3. Монотонні послідовності. Теорема Веєрштраса
- •3.4. Число
- •3.5. Підпослідовності
- •3.6. Фундаментальні послідовності. Критерій Коші
- •3.7. Найбільша і найменша часткова границя
- •4. Границя і неперервність функції
- •4.1. Основні елементарні функції
- •4.2. Границя функції
- •4.2.1. Лівостороння й правостороння границі
- •4.3. Нескінченно малі й нескінченно великі функції
- •4.4. Властивості функцій, що мають границю
- •4.5. Критерій Коші існування границі функції
- •4.6. Неперервність функції
- •4.6.1. Неперервність суперпозиції функцій
- •4.6.2. Одностороння неперервність
- •4.6.3. Класифікація точок розриву функції
- •4.7. Границі і неперервність монотонних функцій
- •4.8. Неперервність елементарних функцій
- •4.9. Важливі границі
- •4.10. Порівняння функцій. Еквівалентні функції
- •5. Неперервні функції на відрізках
- •5.1. Рівномірна неперервність. Теорема Кантора
- •6. Диференціальне обчислення функції однієї змінної
- •6.1. Означення похідної
5.1. Рівномірна неперервність. Теорема Кантора
Означення.
Нехай функція
визначена на множині
.
Говорять, що
рівномірно неперервна на
,
якщо
![]() :
:
![]() ,
то виконується нерівність
.
,
то виконується нерівність
.
Теорема
Кантора. Якщо
функція
![]() неперервна на відрізку
неперервна на відрізку
![]() ,
то вона і рівномірно неперервна на цьому
відрізку.
,
то вона і рівномірно неперервна на цьому
відрізку.
Доведення.
Припустимо
противне, тобто
![]()
![]()
![]()
![]() ,
але
,
але
![]() .
.
Розглянемо
послідовність додатних чисел
![]() ,
,
![]() .
За припущенням з виконання нерівності
.
За припущенням з виконання нерівності
![]() випливає, що
випливає, що
![]() .
.
Розглянемо
обмежену послідовність
![]() .
За лемою Больцано – Веєрштраса з неї
можна виділити збіжну підпослідовність
.
За лемою Больцано – Веєрштраса з неї
можна виділити збіжну підпослідовність
![]() .
Нехай
.
Нехай
![]()
![]() .
.
Розглянемо
![]() .
Оскільки
.
Оскільки
![]() ,
то при
,
то при
![]()
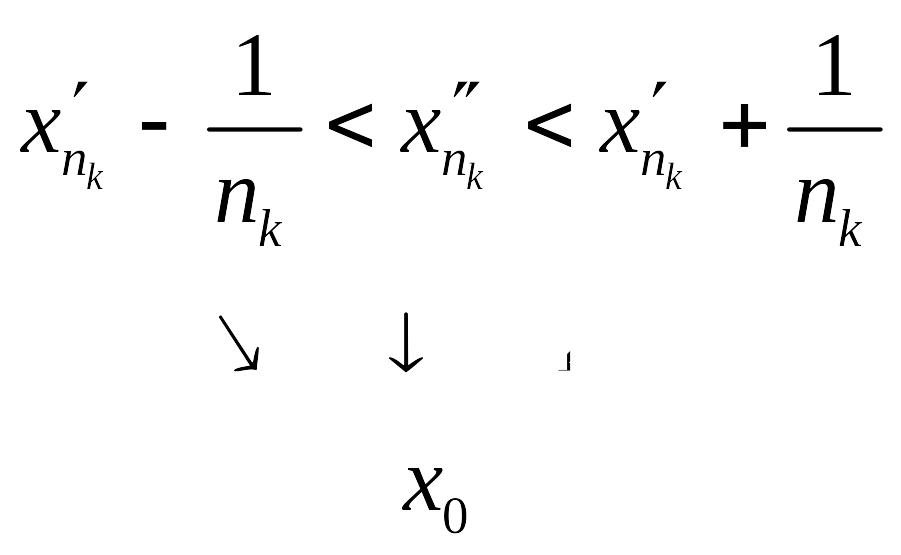 .
.
Отже,
![]() .
З неперервності функції
маємо,
.
З неперервності функції
маємо,
![]() тобто
тобто
![]() ,
.
З іншого боку
,
.
З іншого боку
![]() за припущенням. Одержали суперечність.
Значить, наше припущення неправильне.
Отже, функція рівномірно неперервна на
.
за припущенням. Одержали суперечність.
Значить, наше припущення неправильне.
Отже, функція рівномірно неперервна на
.
Зрозуміло, що будь-яка рівномірно неперервна функція на множині є неперервною в кожній точці множини . Теорема Кантора стверджує, що обернене є правильним для , якщо є відрізком.
6. Диференціальне обчислення функції однієї змінної
6.1. Означення похідної
Означення.
Нехай функція
![]() визначена в околі точки
визначена в околі точки
![]() і
і
![]() –довільна
точка цього околу. Якщо існує границя
–довільна
точка цього околу. Якщо існує границя
![]() ,
то вона називається похідною функції
в точці
(при
,
то вона називається похідною функції
в точці
(при
![]() )
і позначається
)
і позначається
![]() ,
тобто
,
тобто
![]() .
.
Позначимо
приріст аргументу
![]() і приріст функції
в точці
через
і приріст функції
в точці
через
![]() .
Одержимо
.
Одержимо
![]()
![]() .
.
Тобто,
похідна функції
![]() в точці
дорівнює границі відношення приросту
функції в точці
до приросту аргументу в цій точці при
прямуванні приросту аргументу до нуля.
в точці
дорівнює границі відношення приросту
функції в точці
до приросту аргументу в цій точці при
прямуванні приросту аргументу до нуля.
