4.8. Неперервність елементарних функцій

1. Будь-який многочлен є неперервним на всій числовій прямій.

Якщо , то неперервна. Справді, для .

Функція неперервна на числовій прямій. Дійсно, для . , якщо - неперервна.

Функція - неперервна, як добуток неперервних функцій .

Многочлен - одержано з функцій і за допомогою арифметичних операцій, отже, він є неперервним на всій числовій прямій.

2. Дробово-раціональна функція , де - неперервні многочлени, є неперервною для : .

3. Ірраціональні і дробово-ірраціональні функції неперервні. - неперервна при і , тоді неперервна на .

- неперервна, як суперпозиція неперервних функцій.

4. Тригонометричні і обернені тригонометричні функції неперервні.

.

, .

.

З останньої нерівності випливає, що (справедливо для ).

Далі, нехай

і - неперервна на .

- неперервна на .

и неперервні на своїх областях визначення.

, , , - неперервні за наслідком як обернені функції до неперервних.

5. - неперервна. Доведемо, що . Нехай , тоді , , . Для : виконується , , отже, . Для : виконується , отже , , тобто .

Нехай , . Отже, . Це означає, що , отже, - неперервна.

6. - неперервна, як обернена до (неперервної і монотонної).

Теорема. Будь-яка елементарна функція неперервна в своїй області визначення.

4.9. Важливі границі

1. .

2. .

3. .

4. .

5. .

Доведемо першу важливу границю .

Відомо, що при .

Тоді і, оскільки,

, то .

Звідси при за теоремою про двох міліціонерів одержимо:

.

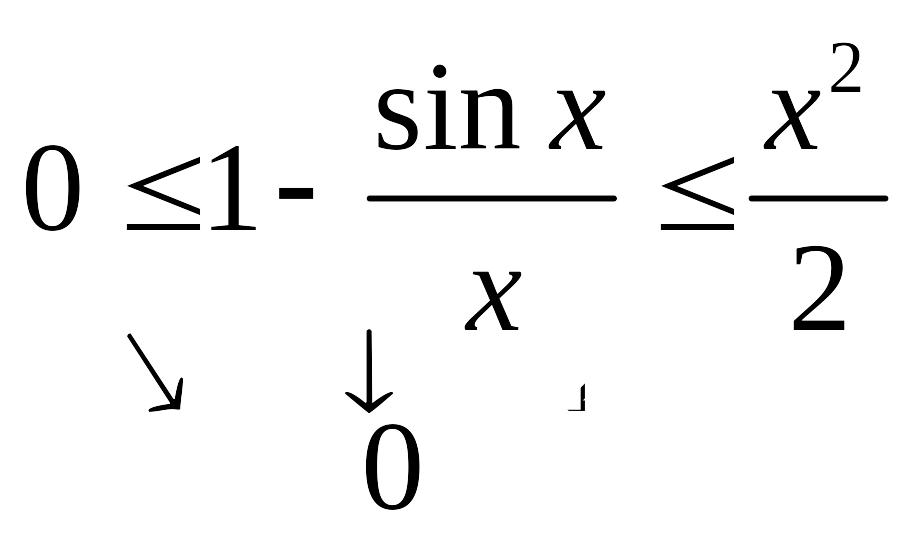Отже, .

Наслідки.

1) ;

2) ;

3) .

Доведемо другу важливу границю .

Нехай , . Тоді .

.

За означенням границі за Гейне .

Нехай . Позначимо .

Тоді

.

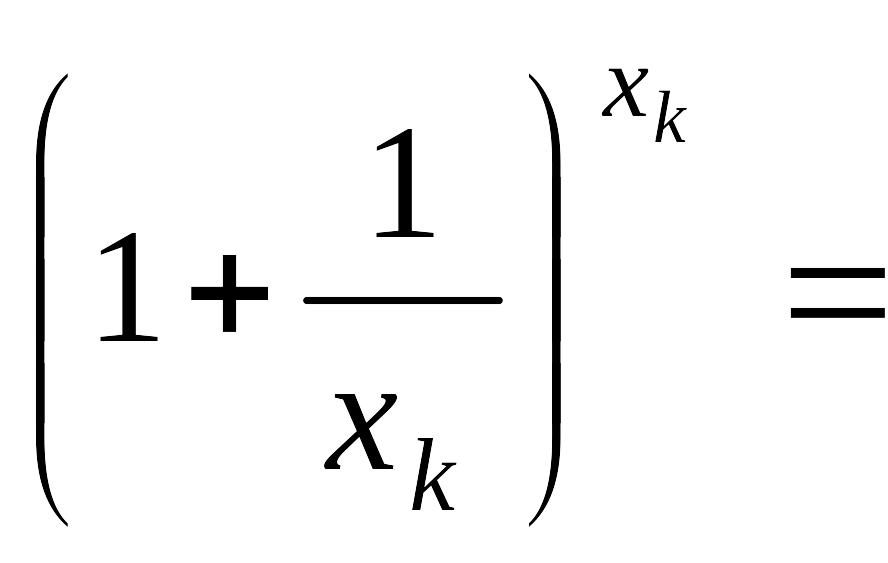
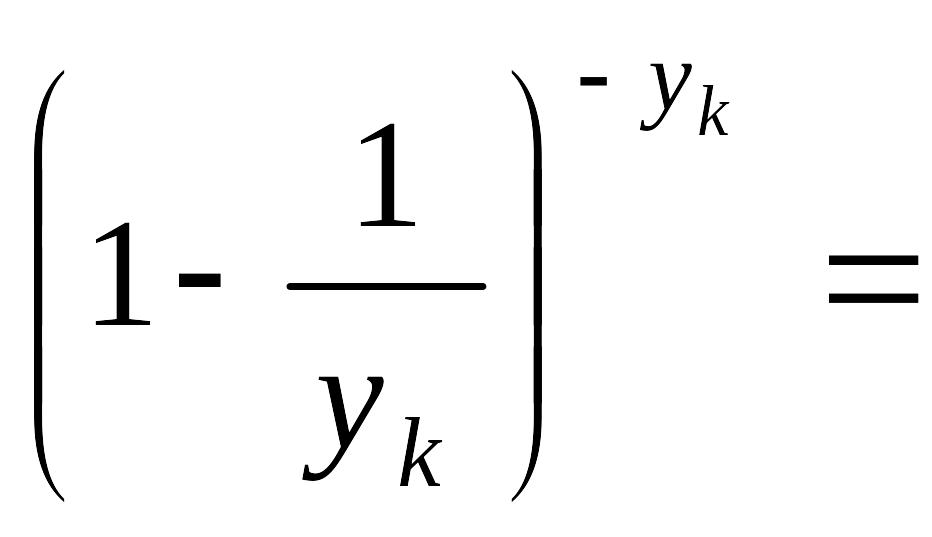
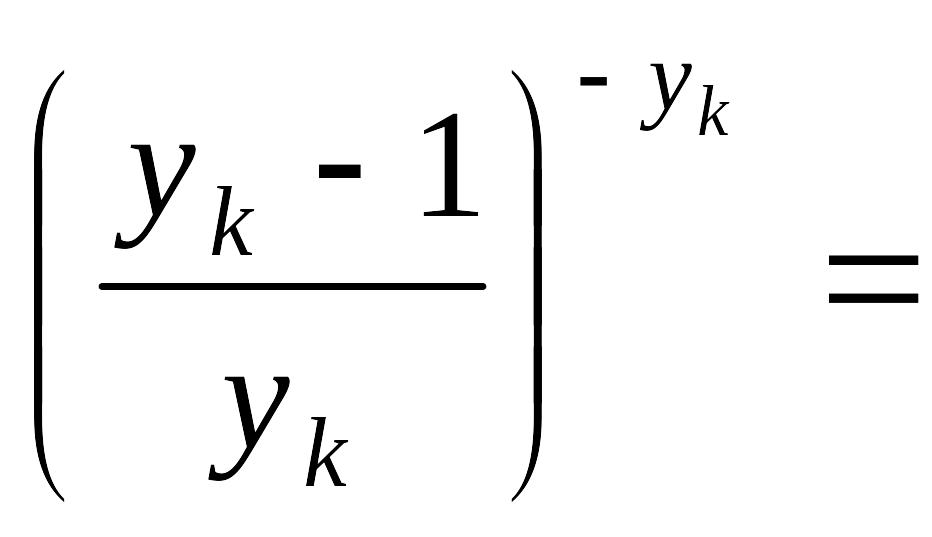
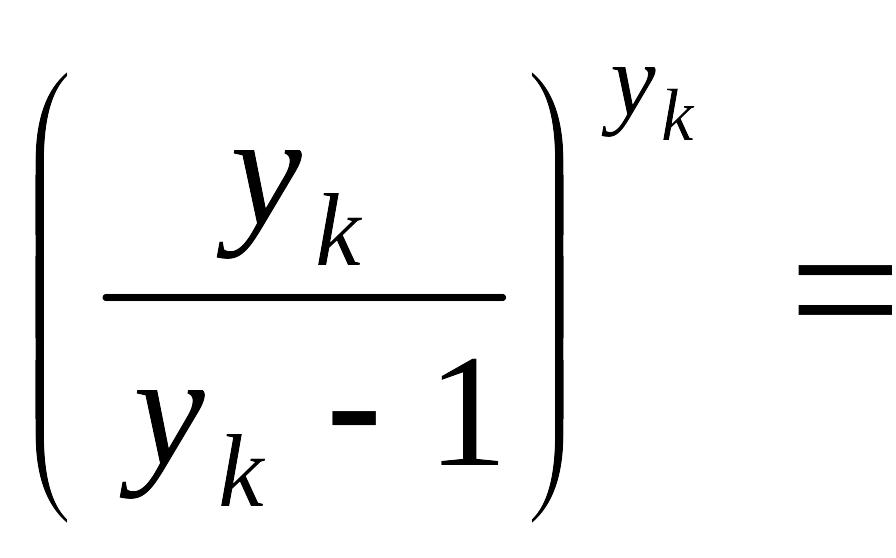
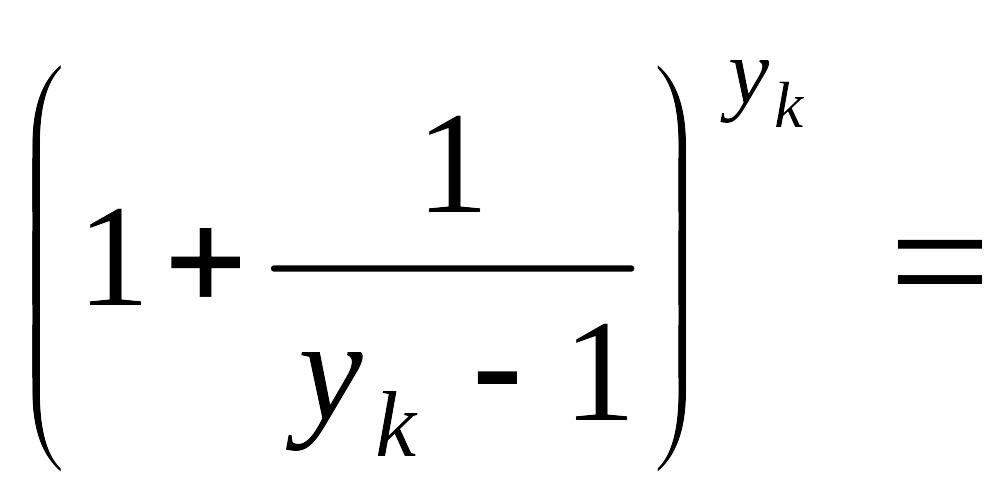
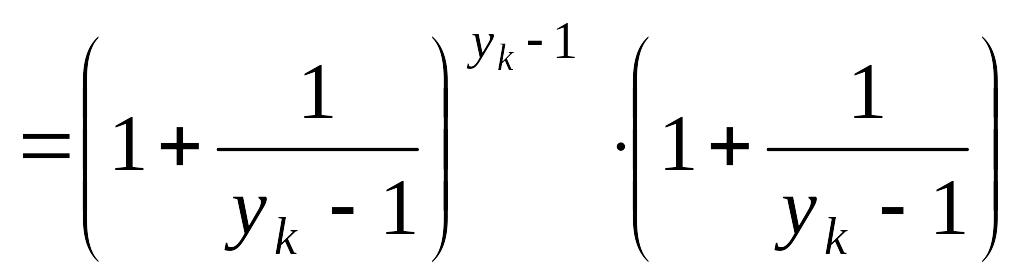
За означенням границі за Гейне .

Таким чином або .

Доведемо .

Дійсно, . Зважаючи на неперервність функції і одержимо .

Доведемо .

Нехай , значить, .

Отже, .

Доведемо .

Нехай .

.

Отже,

.

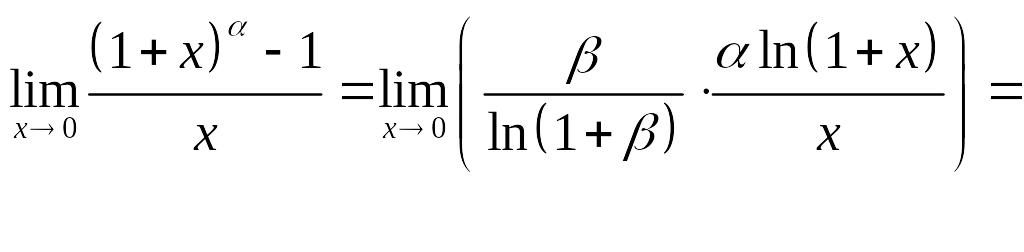
4.10. Порівняння функцій. Еквівалентні функції

Означення. Функції і називаються еквівалентними при , якщо . При цьому пишуть ~ , .

Теорема. Нехай ~ , і ~ , , тоді:

1) ;

2)

при умові, що границі, які розглядаються, існують (скінченні чи нескінченні).

Доведення.

Доведемо тільки друге твердження теореми.

.

Означення. Кажуть, що функція є о-мале від і пишуть при , якщо .

У випадку, коли і – нескінченно малі при , то кажуть, що є нескінченно мала більш високого порядку, ніж , якщо при .

Теорема. Для того щоб виконувалося співвідношення ~ , при необхідно і достатньо, щоб виконувалася рівність

= + при .

Доведення.

Необхідність. Нехай ~ при . Розглянемо границю або = , при .

Достатність. Нехай має місце рівність: = при , тоді

~ при .

Означення. Якщо функцію в околі точки можна подати у вигляді то функція називається головною частиною функції при .

Зокрема, якщо функцію можна подати у вигляді

,

то це означає, що з точністю до нескінченно малих більш високого порядку ніж при функція поводить себе в околі точки як степенева функція .

Приклад. .

Означення. Нехай функції і визначені на множині . Кажуть, що є О-велике від на множині і пишуть , , якщо існує число таке, що виконується нерівність: , .

Зокрема, якщо обмежена на , то пишуть , .