Вариант 19

1) Вычислить определитель .

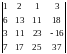2) Найти матрицу , где .

3) Решить систему линейных уравнений тремя способами: а)по формулам Крамера; б)с помощью обратной матрицы; в)методом Гаусса.

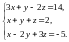
4) Найти площадь параллелограмма и острый угол между диагоналями параллелограмма, построенного на векторах: 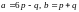, если .

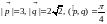5) Найти единичный вектор , перпендикулярный векторам 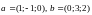и такой, что векторы образуют левую тройку.

6) Даны вершины треугольника А(2; 2; 1), B(1; 1; -2), C(4; 0; -1). Вычислить его длину высоты, проведенную из вершины В и косинус внутреннего угла В.

7) Даны вершины треугольника А(24; 5), В(-2; 5), С(8; -19). Найти точку пересечения высоты, опущенной из вершины В, и медианы, проведенной из вершины С. Найти острый угол между ними и расстояние от этой медианы до вершины А.

8) Найти точку В, симметричную точке А( 1; -12; -1) относительно прямой .

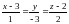9) Даны вершины треугольника А(-6; -1; 3), В(-30; 11; -9), С(-20; 1; -15) . Найти канонические уравнения высоты и медианы, проведенных из вершины С, а также острый угол между ними.

10) Составить уравнение плоскости, проходящей через точку А(-4; -3; -1) перпендикулярно прямой .

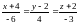11) Даны вершины тетраэдра A( 3; 5 ; 8), B( 0; 8; 3), C( 2; 8; 2), D( 6; 0 ; 9). Найти высоту тетраэдра, опущенную из вершины D, угол между гранью ABD и основанием ABC и угол между ребром AD и плоскостью основания АВС.

12) Установить, что уравнени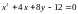е определяет параболу, и найти координаты ее вершины, величину параметра р и уравнение директрисы. Изобразить эту линию на чертеже.

Вариант 20

1) Вычислить определитель .

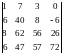2) Найти матрицу , где .

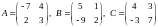3) Решить систему линейных уравнений тремя способами: а)по формулам Крамера; б)с помощью обратной матрицы; в)методом Гаусса.

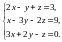
4) Найти площадь параллелограмма и острый угол между диагоналями параллелограмма, построенного на векторах: 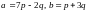, если .

5) Найти единичный вектор , перпендикулярный векторам 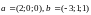и такой, что векторы образуют правую тройку.

6) Даны вершины треугольника А(2; -2; 2), B(3; 5; -7), C(4; 8; 0). Вычислить его высоту, проведенную из вершины В и косинус внутреннего угла В.

7) Даны вершины треугольника А(16; -5), В(5; 5), С(0; -9). Найти точку пересечения высоты, опущенной из вершины В, и медианы, проведенной из вершины С. Найти острый угол между ними и расстояние от этой медианы до вершины А.

8) Найти точку В, симметричную точке А( 8; -8; 1) относительно прямой .

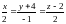9) Даны вершины треугольника А(-8; -2; -3), В(-32; 10; -15), С(-22; 0; -21) . Найти канонические уравнения высоты и медианы, проведенных из вершины С, а также острый угол между ними.

10) Составить уравнение плоскости, проходящей через точку А(-2; 4; 3) перпендикулярно вектору .

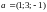11) Даны вершины тетраэдра A( 7; 3; 7), B( 9; 6; 4), C( 7 ; 6 ; 3), D( 0; 3; 5). Найти длину высоты тетраэдра, опущенную из вершины D, угол между гранью ABD и основанием ABC и угол между ребром AD и плоскостью основания АВС.

12) Установить, что уравнение определяет параболу, и найти координаты ее вершины, величину параметра р и уравнение директрисы. Изобразить эту линию на чертеже.