Рациональное число (лат. ratio — отношение, деление, дробь) — число, представляемое несократимой обыкновенной дробью  , где числитель m — целое число, а знаменатель n — натуральное число. Такую дробь следует понимать как результат деления m на n, даже если нацело разделить не удаётся. В реальной жизни рациональные числа используются для счёта частей некоторых целых, но делимых объектов, например, тортов или других продуктов, разрезаемых на несколько частей, или для грубой оценки пространственных отношений протяжённых объектов.

Два отрезка, имеющие общую меру, называются соизмеримыми, а не имеющие   общей меры — несоизмеримыми.

Иррациона́льное число́ — это вещественное число, которое не является рациональным, то есть которое не может быть представленным в виде дроби  , где m — целое число, n — натуральное число. О существовании иррациональных чисел, точнееотрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например,несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа  .

Периодическая дробь

        бесконечная десятичная дробь, в которой, начиная с некоторого места, стоит только периодически повторяющаяся определённая группа цифр. Например, 1,3181818...; короче эту дробь записывают так: 1,3(18), то есть помещают период в скобки (и говорят: «18 в периоде»). П. д. называется чистой, если период начинается сразу после запятой, например 2(71) = 2,7171..., и смешанной, если после запятой имеются цифры, предшествующие периоду, например 1,3(18). Роль П. д. в арифметике обусловлена тем, что при представлении рациональных чисел, то есть обыкновенных (простых) дробей, десятичными дробями, всегда получаются либо конечные, либо периодические дроби. Точнее: конечная десятичная дробь получается в том случае, когда знаменатель несократимой простой дроби не содержит других простых множителей, кроме 2 и 5; во всех других случаях получается П. д., и притом чистая, если знаменатель данной несократимой дроби вовсе не содержит множителей 2 и 5, и смешанная, если хотя бы один из этих множителей содержится в знаменателе. Всякая П. д. может быть обращена в простую дробь (то есть она равна некоторому рациональному числу). Чистая П. д. равна простой дроби, числителем которой служит период, а знаменатель изображается цифрой 9, написанной столько раз, сколько цифр в периоде; при обращении в простую дробь смешанной П. д. числителем служит разность между числом, изображаемым цифрами, предшествующими второму периоду, и числом, изображаемым цифрами, предшествующими первому периоду; для составления знаменателя надо написать цифру 9 столько раз, сколько цифр в периоде, и приписать справа столько нулей, сколько цифр до периода. Эти правила предполагают, что данная П. д. правильная, то есть не содержит целых единиц; в противном случае целая часть учитывается особо.

         Примеры:

        

         

         Известны также правила определения длины периода П. д., соответствующей данной обыкновенной дроби. Например, для дроби a/p, где р — простое число и 1 ≤ a ≤ p — 1, длина периода является делителем р — 1. Так, для известных приближений к числу (см. Пи) ²²/₇ и³⁵⁵/₁₁₃ период равен 6 и 112 соответственно.

Действительные (вещественные) числа представляют собой расширение множества рациональных чисел, замкнутое относительно некоторых (важных для математического анализа) операций предельного перехода. Множество вещественных чисел обозначается  . Его можно рассматривать как пополнение поля рациональных чисел   при помощи нормы, являющейся обычнойабсолютной величины. Кроме рациональных чисел,   включает множество иррациональных чисел  , не представимых в виде отношения целых.

Абсолю́тная величина́ или мо́дуль, обозначается  . В случае вещественногоаргумента — непрерывная кусочно-линейная функция, определённая следующим образом:

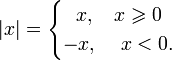
Обобщением этого понятия является модуль комплексного числа  , также иногда называемый абсолютной величиной^[1]. Он определяется по формуле:

Абсолютной величиной действительного числа или модулем действительного числа aназывается само это число, если a  0, и число –a, если a < 0. Модуль числа a обозначаетсяa:

Например,  – 3 =  – 3, так как  – 3 > 0 ( = 3,14);

–3,7 = – (–3,7) = 3,7, так как –3,7 < 0.

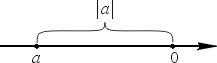
Геометрически a означает расстояние между точками a и 0 на координатной прямой.

Если каждому натуральному числу n поставлено в соответствие некоторое вещественное число    то говорят, что заданачисловая последовательность   Кратко она обозначается символом      называют n-м членом последовательности. Совокупность этих чисел называют множеством значений последовательности.

Постоянное число a называется пределом последовательности x₁ , x₂ , ..., x_n , ... .или пределом переменной x_n , если для сколь угодно малого положительного числа e найдется такое натуральное число N (т.е номер N), что все значения переменной x_n, начиная с x_N, отличаются от a по абсолютной величине меньше, чем на e. Данное определение кратко записывается так:

| x_n - a |<       (2)

при всех n  N, или, что то же самое,

       (3)

Определение 1 (на «языке последовательностей», или по Гейне).

Число А называется пределом функции у=ƒ(х) в топке x₀ (или при х х_о), если для любой последовательности допустимых значений аргумента x_n, n є N (x_nx₀), сходящейся к х_опоследовательность соответствующих значений функции ƒ(х_n), n є N, сходится к числу А

В этом случае пишут        или ƒ(х)—>А при х→х_о. Геометрический смысл предела функции:  означает, что для всех точек х, достаточно близких к точке х_о, соответствующие значения функции как угодно мало отличаются от числа А.

Определение 2 (на «языке ε», или по Коши).

Число А называется пределом функции в точке х_о (или при х→х_о), если для любого положительного ε найдется такое положительное число δ, что для все хх_о, удовлетворяющих неравенству |х-х_о|<δ, выполняется неравенство |ƒ(х)-А|<ε.

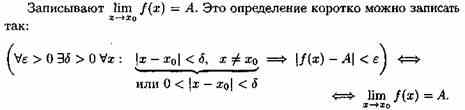
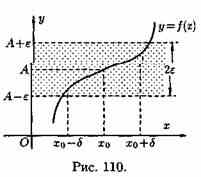
Геометрический смысл предела функции:

если для любой ε-окрестности точки А найдется такая δ-окрестность точки х_о, что для всех ххо из етой  δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε , у=А-ε (см. рис. 110). Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).

Теорема 2. Всякая сходящаяся последовательность является ограниченной.

Доказательство. Пусть {xn} - сходящаяся последовательность и a ее предел. Фиксируем некоторое положительное число ε и по нему номер N такой, что ∣xn−a∣<ε  при n≥N  или, a−ε<xn<a+ε при n≥N . Обозначим через A наибольшее из следующих (N+1) чисел: ∣a−ε∣,∣a+ε∣,∣ ∣  x1∣ ∣  ,∣ ∣  x2∣ ∣  ,...,∣ ∣  хN−1∣ ∣   . Тогда, очевидно, ∣xn∣≤A  для всех номеров n, а это и доказывает ограниченность последовательности {xn}. Теорема доказана.

Если функция y = f(x) такая, что   для всех x в некоторой окрестности точки a, причем функции φ(x) и ψ(x) имеют одинаковый предел при  , то существует предел функции y = f(x)при  , равный этому же значению, то есть

Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.

Бином Ньютона. Это формула, представляющая выражение ( a + b ) ⁿ  при положительном целом  n  в виде многочлена:

            

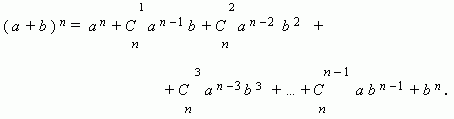
Заметим, что сумма показателей степеней для  a  и  b  постоянна и равна n.

e — математическая константа, основание натурального логарифма,трансцендентное число. Иногда число e называют числом Эйлера иличислом Непера. Обозначается строчной латинской буквой «e». Численное значение^[1]:

(последовательность A001113 в OEIS)

Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики.

Для всякой системы вложенных отрезков

существует хотя бы одна точка c, принадлежащая всем отрезкам данной системы.

Если, кроме того, длина отрезков системы стремится к нулю:

то c — единственная общая точка всех отрезков данной системы.

Точная верхняя граница (верхняя грань) и точная нижняя граница (нижняя грань) — обобщение понятий максимума и минимума множества соответственно.

Точной (наименьшей) верхней гранью (границей), или супре́мумом (лат. supremum — самый высокий) подмножества Xупорядоченного множества (или класса) M, называется наименьший элемент M, который равен или больше всех элементовмножества X. Другими словами, супремум — это наименьшая из всех верхних граней. Обозначается sup X.

Более формально:

 — множество верхних граней X, то есть элементов M, равных или больших всех элементов X

Точной (наибольшей) нижней гранью (границей), или и́нфимумом (лат. infimum — самый низкий) подмножества Xупорядоченного множества (или класса) M, называется наибольший элемент M, который равен или меньше всех элементовмножества X. Другими словами, инфимум — это наибольшая из всех нижних граней. Обозначается inf X.

[Править]Замечание

Эти определения ничего не говорят о том, принадлежит ли sup X и inf X множеству X или нет. В случае  , говорят, что s является максимумом X. В случае  , говорят, что i является минимумом X.

Теорема 6 (существование предела у монотонной функции). Для того чтобы неубывающая на множестве E функция f:E R имела предел при xs, необходимо и достаточно, чтобы она была ограничена сверху, а для того чтобы она имела предел при x i необходимо и достаточно, чтобы она была ограничена снизу.

Первая формулировка

Пусть предложена последовательность точек пространства  :

и пусть эта последовательность ограничена, то есть

где C > 0 — некоторое число.

Тогда из данной последовательности можно выделить подпоследовательность

которая сходится к некоторой точке пространства  .

Теорему Больцано — Вейерштрасса в такой формулировке иногда называют принципом компактности ограниченной последовательности.

[Править]Расширенный вариант первой формулировки

Нередко теорему Больцано — Вейерштрасса дополняют следующим предложением.

Если последовательность точек пространства   неограничена, то из нее можно выделить подпоследовательность, имеющую предел  .

Для случая n = 1 эту формулировку можно уточнить: из любой неограниченной числовой последовательности можно выделить подпоследовательность, имеющую пределом бесконечность определенного знака (  или  ).

Таким образом, всякая числовая последовательность содержит подпоследовательность, имеющую предел в расширенном множестве действительных чисел  .

[Править]Вторая формулировка

Следующее предложение является альтернативной формулировкой теоремы Больцано — Вейерштрасса.

Всякое ограниченное бесконечное подмножество E пространства   имеет по крайней мере одну предельную точку в  .

Более подробно, это означает, что существует точка  , всякая окрестность U_ε(x₀) которой содержит бесконечное число точек множества E.

Функциональные последовательности

Определение. Если каждому натуральному числу n ставится в соответствие по некоторому закону функция f_n(x), определенная на множестве  , то говорят, что на множестве X задана функциональная последовательность{f_n(x)}. Множество X называется областью определения последовательности {f_n(x)}.

Определение. {f_n(x)} сходится в точке x₀, если числовая последовательность {f_n(x₀)} сходится. Множество всех точек x₀ в которых {f_n(x)} сходится, называется областью сходимости функциональной последовательности {f_n(x)}.

D - область сходимости {f_n(x)}. Пусть   - обозначение предельного значения. Совокупность всех предельных значений есть функция, определенная на множестве D. Эта функция f(x) называется предельной функцией последовательности {f_n(x)}.

Замечание. Точечная сходимость {f_n(x)} на некотором множестве D не гарантирует сохранения свойств членов последовательности (например, свойства непрерывности, интегрируемости и т.д.)

Функция — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).

Математическое понятие функции выражает интуитивное представление о том, как однавеличина полностью определяет значение другой величины. Так значение переменной xоднозначно определяет значение выражения x², а значение месяца однозначно определяет значение следующего за ним месяца, также любому человеку можно сопоставить другого человека — его отца. Аналогично, некоторый задуманный заранееалгоритм по варьируемым входным данным выдаёт определённые выходные данные.

Часто под термином «функция» понимается числовая функция; то есть функция которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.