9.Числовая последовательность. Определение предела числовой последовательности.
Если
для каждого элмента из некоторого
множества взаимнооднозначно сопоставлено
натуральное число (т.е. задан номер), то
говорят, что задана последовательность{xn},
xn
– общий элемент последовательности.
Число А
называется пределом числовой
последовательности {xn},
если для любого ε>0
существует номер N=N(ε)>0
такой, что
для всех номеров n>N
выполняется неравенство |
xn
–A|
< ε.
.
Последовательность, имеющая предел,
называется сходящейся, в противном
случае – расходящейся.
12,13.
14. Производная ф-ции. Смысл.
Производной ф-ции y=f(x) в тч. Х0 наз. предел отношения приращения этой ф-ции к приращению аргумента , когда последнее стремится к нулю.
Формула
выражает геометрический
смысл производной: производная
от данной ф. в данной точке = tg
угла наклона касательной графика ф-ции
в этой тчк. Производительность труда
есть производная объема продукции по
времени. Рассмотрим некоторые понятия,
иллюстрирующие экономический
смысл производной.
Пусть y(x) – ф-ция, характеризующая,
например, издержки производства, где
x - количество выпускаемой продукции.
Тогда отношение
описывает
средние издержки, приходящиеся на одно
изделие. Средняя величина обозначается
Ay или Af (от английского "average".)
Среднее приращение, средний прирост,
средняя скорость изменения определяется
отношением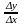
.
Производная
выражает предельные издержки производства.
Величину Mf(x) = y' наз. мгновенным приростом
или мгновенной скоростью изменения y.
Аналогично можно определ. предельную
выручку, предельный доход, предельную
полезность и др. предельные величины.
Правила
дифференцирования:
1.Производная
сум.(разности) двух дифференц-ых ф-ций
=сумме(разности) производных этих ф-ций
2.Производная
произведения двух диффиренц-ых ф-ций
= произведению первой ф-ции на роизводную
второй + произведение второй ф-ции на
производную первой:
3.Производная
частного двух
дифференц-ых
ф-ций определ. формулой: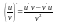
где
16. Произв. Сложной и обр. Ф-ции.
Производная
сложной ф.:Если
и
-дифференцируемые
ф. своих аргументов, то производная
сложной ф.
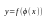сущ. и равна произведению производной
этой ф-ции по промежуточному аргументу
на производную промежуточного по
независимой переменной, т.е.
,
.
П
роизводная
обратной ф.:Если y=f(x)
и
-
взимно-обратые дифференцируемые ф-ции
и
,то
Действительно,т.к.
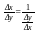,то
17.
Таблица производной
,
,
,
,
,
,
,
,
,
,
,
,
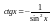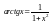19.Первообразная функции. Неопределённый интеграл. Основные свойства неопределённого интеграла
Функция
F
называвается первообразной для функции
А на некотором промежутке X,если
любое x€X,
(x)=f(x)
Задача об отыскании первообразной от данной ф. f решается неоднозначно.
F
(x)=f(x)
(F(x)+C) =F (x)+C =f(x)
Теорема.
Если
F
(x)
и F
(x)-две
любые первообразные для функции f
на промежутке X,
то они могут отличаться лишь на
постоянную,т.е.F
(x)-F
(x)=C=const.
Доказательство.
Пусть F и F -первообразные функции f.
Рассмотрим производную разности:
(
(x)-
(x))`=
(x)-
(x)=f(x)-f(x)≡0.
(x)- (x)=const.
Ч.Т.Д.
(x) – первообразная ф. f, то множество всех её первообразных имеет вид F(x)+C.
Определение. Множество всех первообразных ф.f(x) называется неопредел. интегралом ф. f(x) и обозн. ∫f(x)dx.
Ф-ция f(x) наз. подынтегральной функцией.
Выраж. f(x)dx наз. подынтегральн. выраж.
x- переменная интегрир.
Если F(x)-первообр.ф. f(x), то неопр. интегр.- ∫f(x)dx=F(x)+C.
Основные свойства неопр. интегралов:
1.Производная
неопр. интеграла равна подынтегр. ф-ции;
дифференциал неопр. интеграла равен
подынтегр. выраж.: (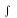
f(x)dx)`=f(x),
d
=f(x)dx.
2.Неопр.
интеграл от дифференциала некот. функции
с точностью до пост. Слагаемого: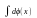
=
+С.
Док – во:
Пусть
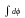(x)=
(x)dx=F(x).На
основании 1св-ва получ.:
(x)=F`(x),
откуда F(x)=
(x)+C,т.е.
(x)=
(x)+C.
3.Пост.
множитель можно вынос. за знак неопр.
интегр:
=k
(k=const,k
0).
4.Если
функция
(x)
и
(x)
имеют первообр. , то ф-ции
(x)
+
(x)
тоже имеют первообр.,причем
(x)+
(x)
dx=
(x)dx+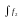
(x)dx.