7.4. Дифференцирование сложной функции

Пусть , где , причем и - дифференцируемые функции. Тогда будет сложной функцией , дифференцируемой по переменной х.

Теорема. Если существуют производные функций и , где , то сложная функция имеет производную в точке , которая вычисляется по формуле:

Здесь х - независимая переменная, а и - промежуточная переменная. Таким образом производная по независимой переменной равна произведению производной функции по промежуточной переменной и производной промежуточной переменной по независимой переменной.

Пример. Вычислить производную функции:

Решение:

Записываем данную функцию в виде степени: и вычисляем:

.

7.5. Дифференцирование функции, заданной неявно

Рассмотрим случай неявно заданной функции, т.е. когда функция задаётся равенством вида . Если в это равенство подставить числовое значение и решить полученное уравнение относительно у, то при определённых условиях можно получить явное значение функции .

Например, равенство определяет явно заданную функцию . Ясно, что не всегда удаётся однозначно выразить у из равенства . Так, например, равенство определяет две явно заданные функции и . Во многих случаях бывает трудно аналитически (в виде формулы) выразить явно у, а иногда и невозможно (например, в случае ).

Для того чтобы найти производную неявной функции, необходимо найти производную от каждого слагаемого функции, учитывая, что у - это есть сложная функция от переменной х, а затем выразить .

Пример. Вычислить производную неявно-заданной функции: _.

В данном случае зависимость между аргументом х и функцией у задана уравнением, которое не разрешено относительно функции у. Чтобы найти производ­ную у', следует дифференцировать по х обе части задан­ного уравнения, считая при этом у функцией от х, а затем полученное уравнение решить относительно искомой производной у'. Имеем

Из полученного равенства, связывающего х, у, и у', находим производную у':

откуда

7.6. Дифференцирование степенно-показательной функции

Для того чтобы найти производную степенно-показательной функции, достаточно дифференцировать ее вначале как степенную, а затем как показательную и полученный результаты сложить.

Пусть .

Найдем .

Учитывая что , получим после преобразований:

Пример. Вычислить производную функции:

Решение.

7.7. Дифференциал функции

Определение. Дифференциалом функции называется главная часть приращения функции, линейная относительно .

Дифференциал функции принято обозначать символом . Таким образом, из определения имеем:

(7.2)

.

Тогда равенство (1) примет вид

т.е. дифференциал функции равен произведению производной функции на дифференциал аргумента.

_{Формула для вычисления приближённых значений имеет вид:}

Примеры решения типовых задач

№ 1. Найти производные следующих функций:

а) , б) , в) , г) ,

д) , е) .

Решение:

а) Перепишем данную функцию, записав слагаемые в виде степени:

.

.

б) Данная функция является показательной, следовательно по формуле

посчитаем производную:

в) Применив формулу , находим:

.

г) Дифференцируя функцию как сложную, находим производную:

д) В соответствии с формулой получаем:

.

е) По аналогии с примером в) находим:

.

№ 2. Вычислить приближённое значение .

Решение

1. Пусть , тогда получим функцию . Представим в следующем виде: , тогда и .

2. Найдём и :

3.

.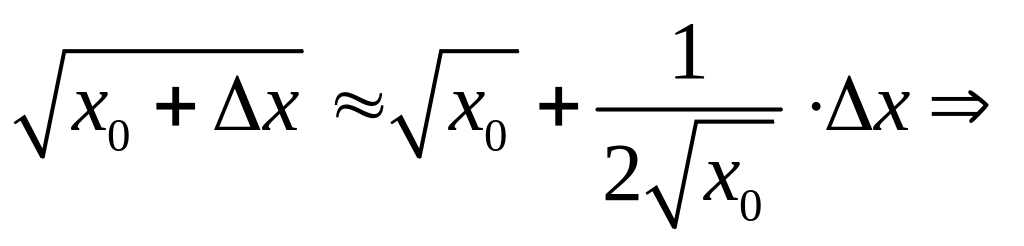