
- •Контрольная работа № 2
- •Раздел IV. Введение в математический анализ
- •Глава 6. Пределы и непрерывность
- •6.1. Предел функции. Бесконечно большие и бесконечно малые величины и их свойства
- •Свойства бесконечно малых функций
- •Свойства бесконечно больших функций
- •6.2. Теоремы о пределах.
- •6.3. Способы раскрытия неопределённостей вида и
- •6.4. Первый и второй замечательные пределы
- •6.5. Непрерывность функции. Точки разрыва
- •Примеры решения типовых задач
- •Контрольный тест по после изучения раздела IV «Введение в математический анализ»
- •Раздел V. Дифференциальное исчисление одной переменной
- •Глава 7. Производная
- •7.1. Задачи, приводящиеся к понятию производной
- •7. 2. Определение производной. Зависимость между непрерывностью и дифференцируемостью функции
- •7.3. Основные правила дифференцирования. Таблица производных
- •Правила дифференцирования
- •7.4. Дифференцирование сложной функции
- •7.5. Дифференцирование функции, заданной неявно
- •7.6. Дифференцирование степенно-показательной функции
- •7.7. Дифференциал функции
- •Примеры решения типовых задач
- •Контрольный тест после изучения главы 7 «Производная»
- •Глава 8. Приложения производной
- •8.1. Признаки возрастания и убывания функции
- •8.2. Экстремум функции
- •8.3. Выпуклость функции. Точки перегиба
- •8.4. Асимптоты графика функции
- •8.5. Схема полного исследование функции методами дифференциального исчисления и построения её графика
- •Пример решения типовой задачи
- •Контрольный тест после изучения главы 8 «Приложения производной»
- •Раздел VI. Функции нескольких переменных
- •Глава 9. Функция двух переменных
- •9.1. Основные определения
- •9.2. Предел и непрерывность функции двух переменных
- •9.3. Частные производные и полный дифференциал функции двух переменных
- •Пример решения типовой задачи
- •Контрольный тест после изучения главы 9 « Функция двух переменных»
- •Задания для контрольной работы № 2
- •Контрольные вопросы к аттестации по предмету
Примеры решения типовых задач
№1. Вычислить пределы следующих функций:
а).
![]() ;
б).
;
б).
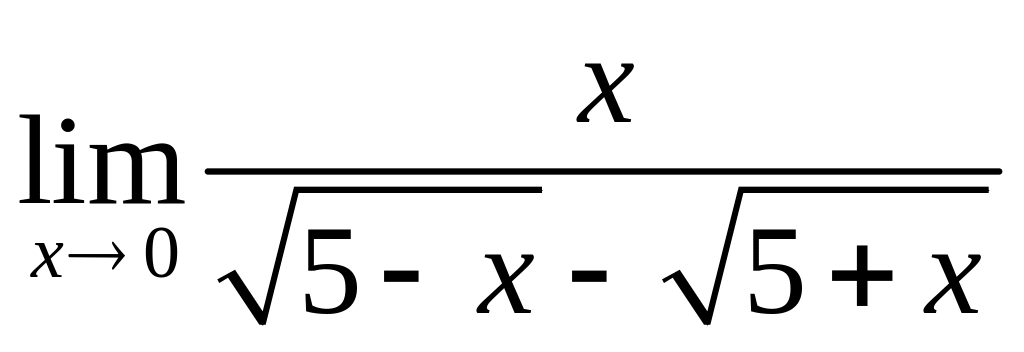 ;
в).
;
в).
![]()
г).
![]() ;
д).
;
д).
![]() ;
е).
;
е).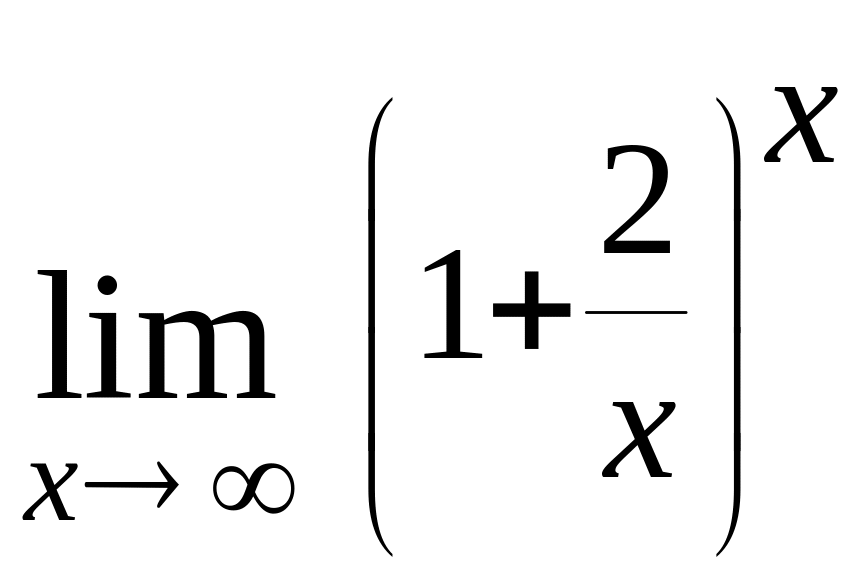 ;
ж).
;
ж).
 .
.
а).
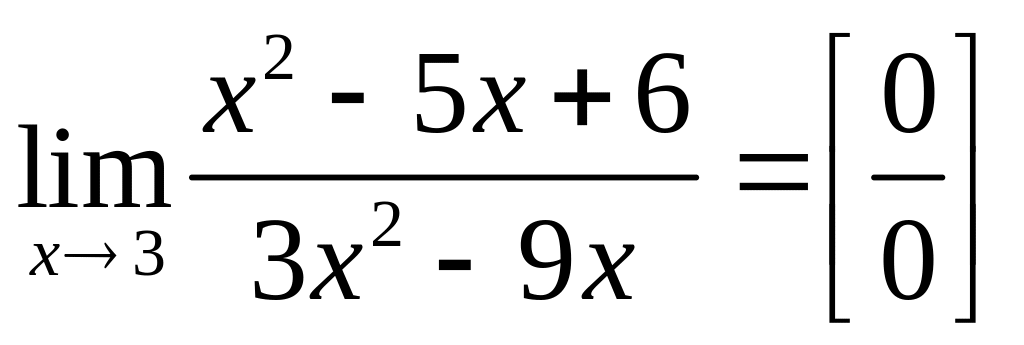 .
.
Разложим
квадратный трехчлен в числителе на
множители по формуле
![]() где x1
и x2
– корни
квадратного уравнения
где x1
и x2
– корни
квадратного уравнения
![]() Разложив на множители и знаменатель,
сократим дробь на
Разложив на множители и знаменатель,
сократим дробь на
![]() получим:
получим:
![]()
б).
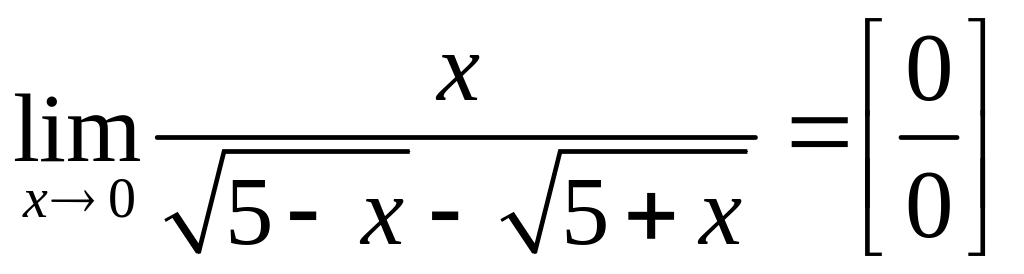 .
.
Пределы
числителя и знаменателя при
![]() равны нулю. Умножив числитель и
знаменатель на сопряженный знаменателю
множитель
равны нулю. Умножив числитель и
знаменатель на сопряженный знаменателю
множитель
![]() и затем сократив дробь на
и затем сократив дробь на
![]() получим:
получим:
![]()
![]() .
.
в). = .
Разделим каждое слагаемое числителя и знаменателя на х4
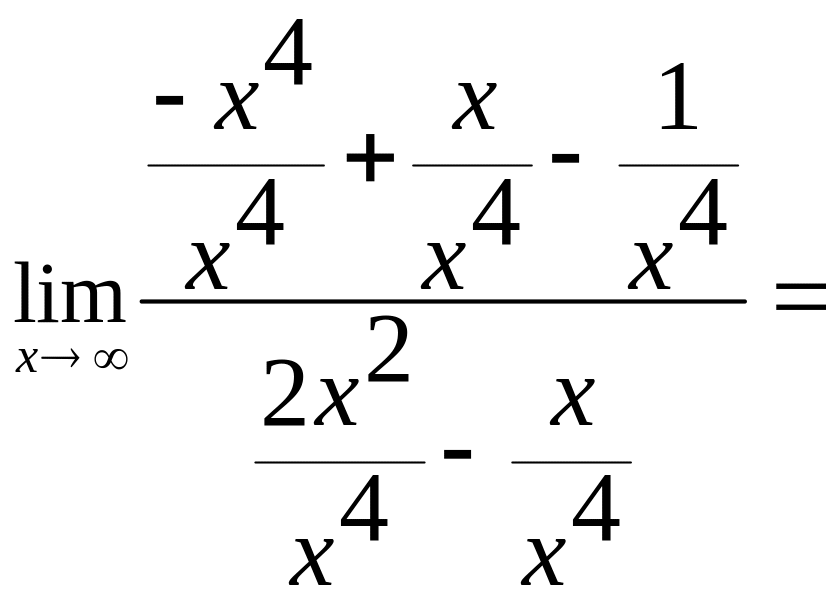
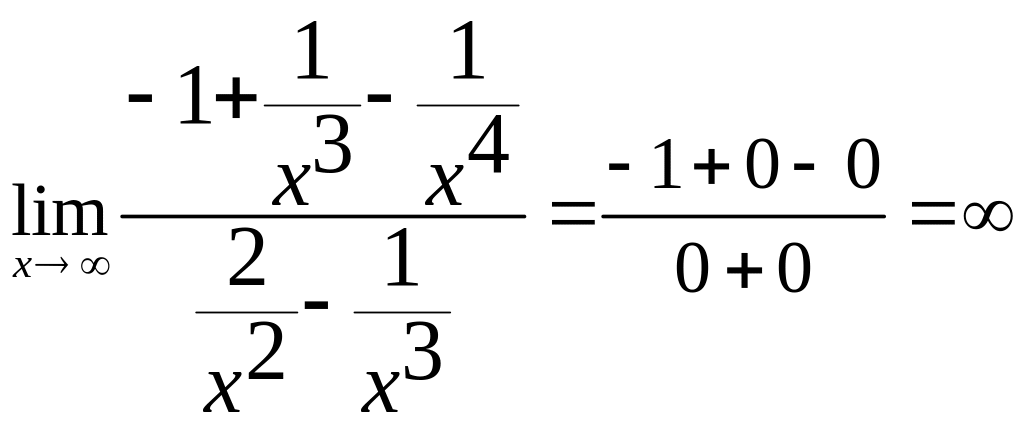
г). =
Разделим каждое слагаемое числителя и знаменателя на х4
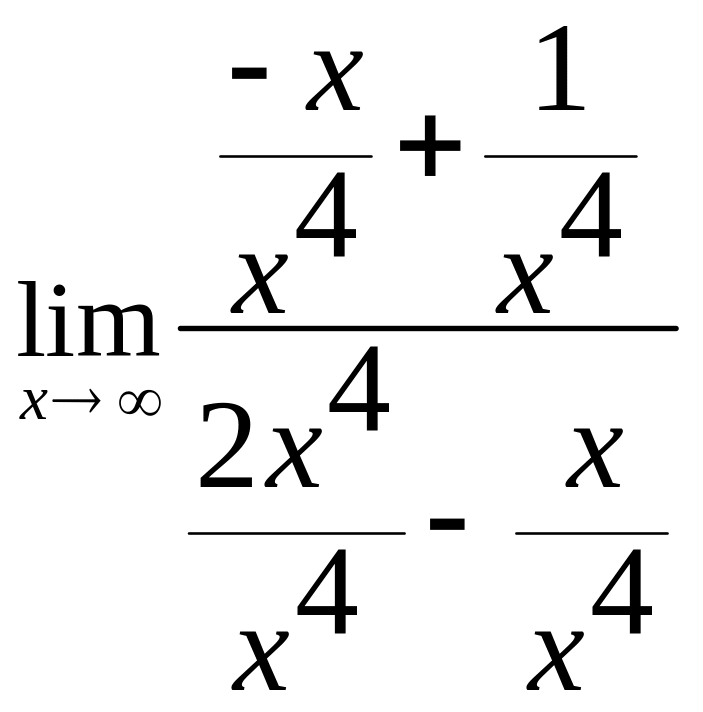 =
=
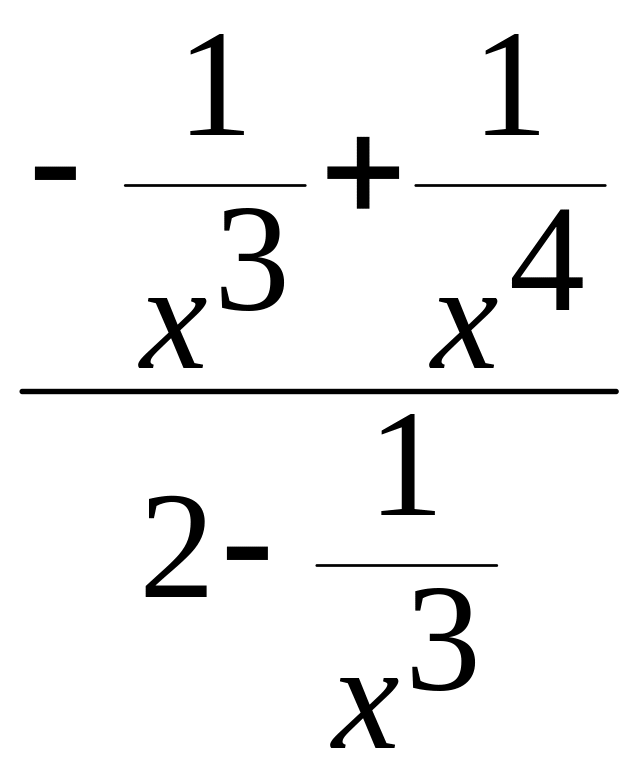 =
=
![]() =
=
![]() .
.
д).
![]() =
.
=
.
Поделим числитель и знаменатель дроби под знаком предела на х, после чего воспользуемся формулой первого замечательного предела, получим:
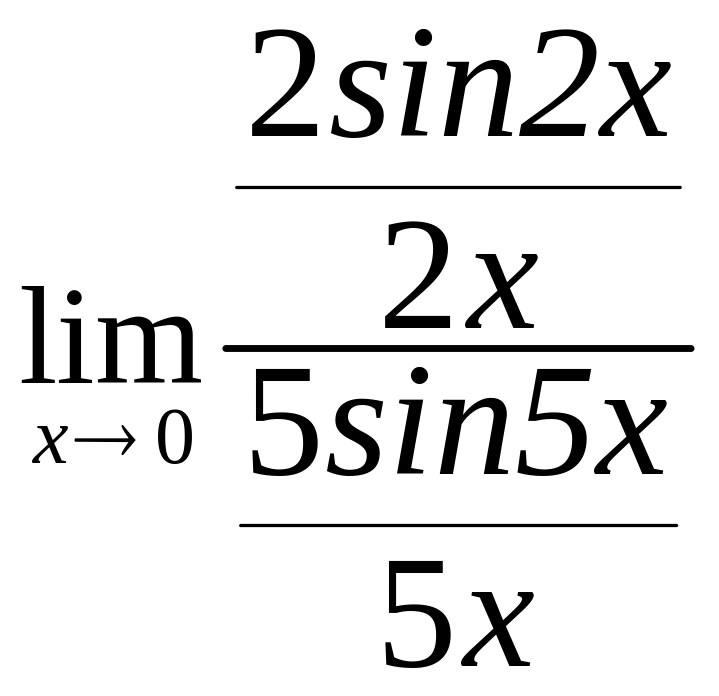 =
=
![]() .
.
е).
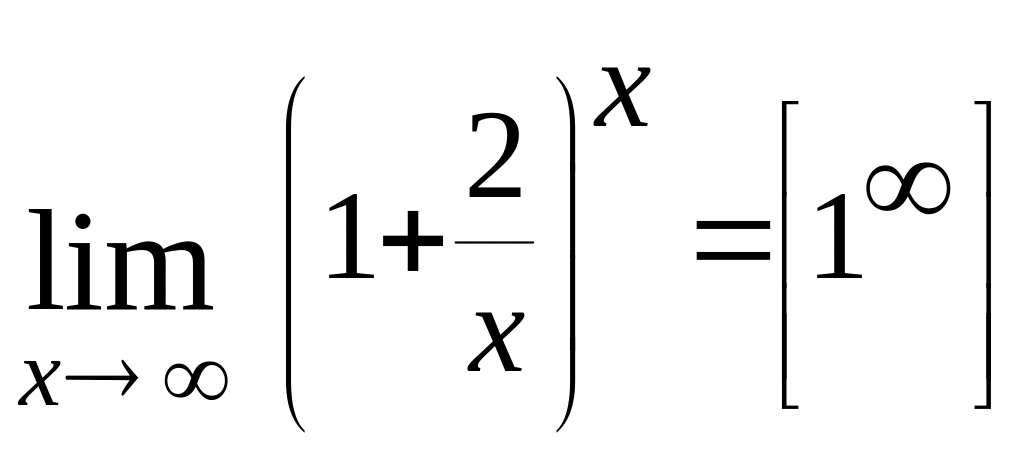 .
.
Сделаем замену у = . Тогда при и исходный предел сводится ко второму замечательному пределу:
![]() =
=
![]() =
=
 =
.
=
.
ж). .
Очевидно,
что
![]()
Тогда:
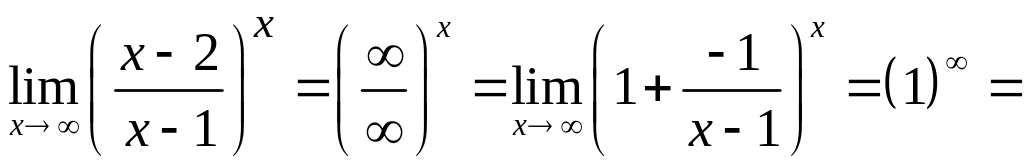
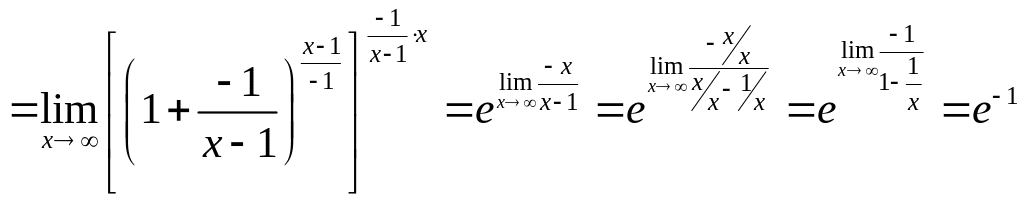
№ 2. Задана функция у = f(x):
1) Исследовать функцию на непрерывность на всей числовой оси.
2) Найти и классифицировать точки разрыва, если они существуют.
3) Построить график функции.
f(x)
=
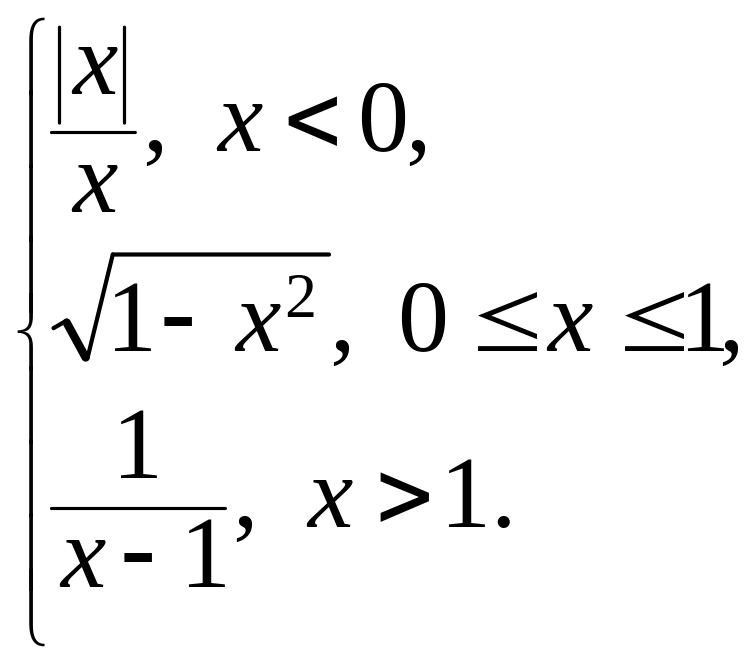
Решение:
Р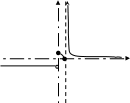 ассмотрим
поведение функции в точках х
= 0, х
= 1.
ассмотрим
поведение функции в точках х
= 0, х
= 1.
Найдем правый и левый предел функции в точке х = 0:
![]() и
и
![]() ,
х=0–
точка разрыва первого рода т.к.пределы
конечны.
,
х=0–
точка разрыва первого рода т.к.пределы
конечны.
Найдем правый и левый предел функции в точке х = 1:
![]() и
и
![]() -
один из пределов равен бесконечности,
значит х=1–точка
разрыва второго рода.
-
один из пределов равен бесконечности,
значит х=1–точка
разрыва второго рода.
Контрольный тест по после изучения раздела IV «Введение в математический анализ»
1.
Вычислить
![]()
1).1/2; 2). -1/3; 3). 2/3; 4).-1; 5). 0.
2.
Функция
![]() ,
определенная на интервале
,
определенная на интервале
![]() ,
называется непрерывной в точке
,
называется непрерывной в точке
![]() ,
если:
,
если:
1).
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
3.
Используя свойства пределов функций,
найти предел
![]()
1) 2; 2) 3; 3) 21; 4)6; 5) 5.
4.
Используя свойства пределов функций,
найти предел
![]()
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() .
.
5. Указать первый замечательный предел.
1)
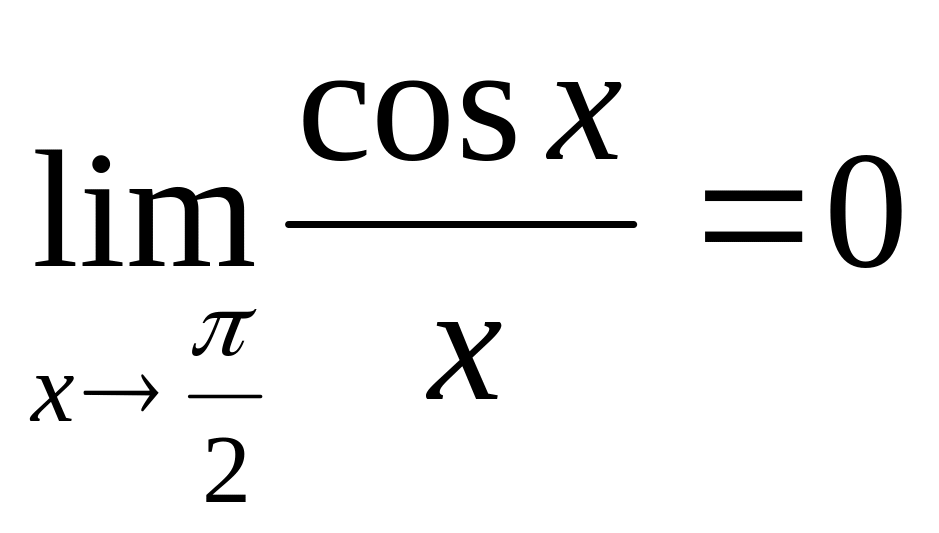 ;
2)
;
2)
![]() ;
3)
;
3)
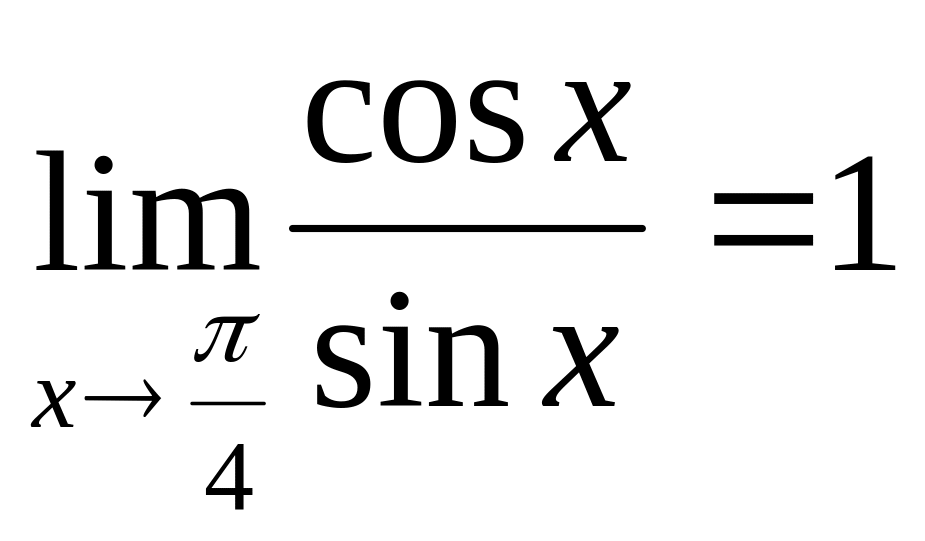 ;
4)
;
4)
![]() .
.
6.
Предел
![]() равен:
равен:
1)
0; 2) 2; 3)
![]() ;
4) 1.
;
4) 1.
7.
Если функция
![]() — функция, непрерывная на отрезке
— функция, непрерывная на отрезке
![]() ,
причем ее значения принадлежат отрезку
,
причем ее значения принадлежат отрезку
![]() ;
;
![]() — функция, непрерывная на отрезке
,
то сложная функция
— функция, непрерывная на отрезке
,
то сложная функция
![]() непрерывна в промежутке:
непрерывна в промежутке:
1)
;
2)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() .
.
8. Указать второй замечательный предел.
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;4)
;4)
![]() .
.
9.
Предел
![]() равен:
равен:
1)
![]() ;
2) 0; 3)
;
2) 0; 3)
![]() ;
4) 2.
;
4) 2.
10.
Предел функции
в точке
существует и равен
![]() ,
если:
,
если:
1)
существует предел справа
![]() ;
;
2)
существует предел слева
![]() ;
;
3) существуют левосторонний и правосторонний пределы.
4)
существуют односторонние пределы,
равные между собой, т.е.
![]() ;
;
11.
Точкой разрыва функции
![]() является точка:
является точка:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() .
.
