Задание для самостоятельного решения

1. Приведите примеры элементарных функций, полиномов, дробно-рациональных функций (правильных и неправильных).

2. Изобразите графики функций:

а)

б)

в)

3. y = f (x) – четная функция. Каким свойством обладает её график?

4. y = f (x) – нечетная функция. Каким свойством обладает её график?

5. Функция – четная. Запишите её в виде формулы, если при x > 0. Как изменится выражение функции , если она нечетная?

6. Изобразите графики функций

7. Имеет ли функция y=lnx обратную? Ответ проиллюстрируйте графически.

8. При каком условии можно говорить об обратной функции для 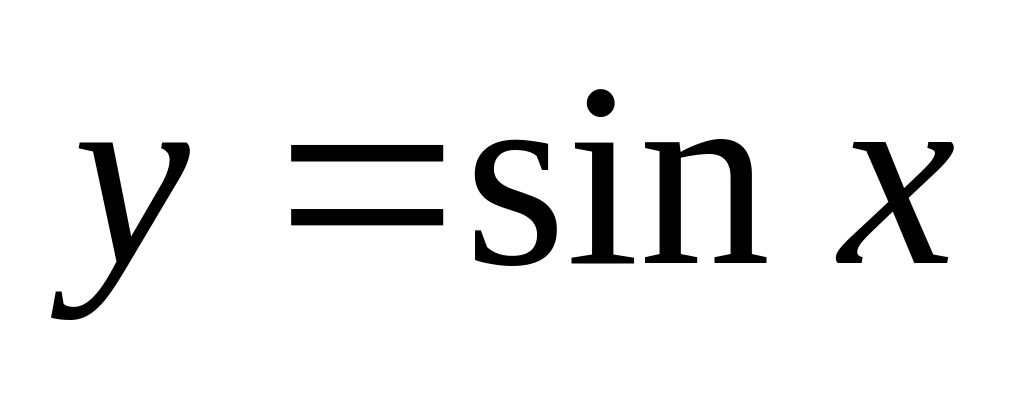? Каков ее график?

9. Запишите сложную функцию h = g ( f (x)), если

Укажите область определения сложной функции.

10. Будет ли задавать сложную функцию выражение ?

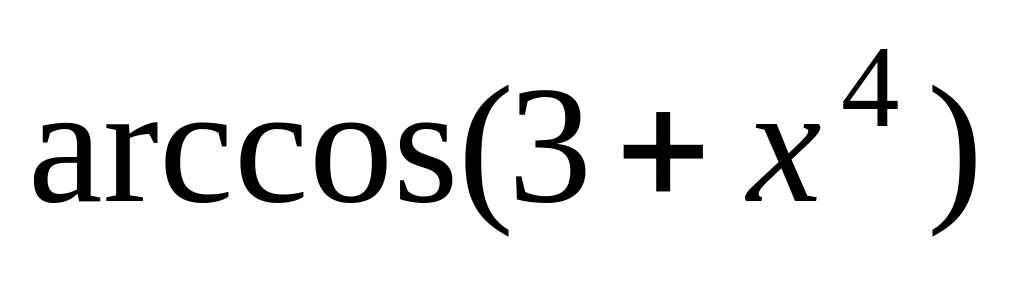3.1.2. Числовая функция нескольких переменных.

Отображение f: ХY называется числовой функцией п переменных, если

Если , то соответствующее значение функции обозначают через

Функцию двух переменных обычно обозначают так: z = f (x, y).

Как и для функции одной переменной, множество Х называется областью определения функции а множество  областью значений. Очевидно, что заданные формулами функции п переменных классифици-руются подобно функциям одной переменной.

При решении прикладных задач физического содержания числовые функции нескольких переменных часто называют скалярными полями. Примерами могут служить поле электростатического потенциала, порожденное системой электрических зарядов v = f (x, y, z), нестационарное температурное поле в неравномерно нагретом теле Т = f (x, y, z, t) и т.п.

Функция двух переменных z = f (x, y) может рассматриваться как функция точки (x, y) плоскости Oxy: каждой паре чисел (x, y) ставится в соответствие аппликата z.

Графиком такой функции называется множество точек

,

о пределяющее, вообще го­воря, некоторую поверхность в (рис. 3.1.4).

Многие поверхности удоб-но представлять уравнением в неявном виде

F(x, y, z) = 0, (3.1.1)

которое в некоторых случаях может быть разрешено отно-сительно z:

z = f (x, y). (3.1.2)

В качестве примера составим уравнение сферы радиуса r с центром в начале координат.

Выберем произвольную точку М(x, y, z), принадлежащую сфере. Тогда , или

т.е.

(3.1.3)

Если в последнем уравнении перенести в левую часть, то получим неявное уравнение вида (3.1.1).

Если (3.1.3) разрешить относительно z, то придем к двум равенствам вида (3.1.2):

каждое из которых определяет полусферу («верхнюю» и «нижнюю»).

Аналогично понятию поверхности в трехмерном пространстве вводится понятие гиперповерхности в п - мерном пространстве Если упорядоченную систему чисел считать координатами некоторой точки Р пространства то уравнение

или

определит гиперповерхность в

Напомним, что  уравнение плоскости в ;  уравнение гиперплоскости в

3.1.3. Вектор-функция скалярного аргумента.

Отображение f: ХY называется вектор-функцией скалярного аргумента, если

Для tX соответствующее значение вектор-функции обозначается через

Из определения следует, что задание одной вектор-функции равносильно заданию п скалярных функций:

(3.1.4)

Рассмотрим частный случай п = 2:

(3.1.5)

Если переменную t интерпретировать как время, то уравнения (3.1.5) будут выражать координаты точки, перемещающейся по плоскости (рис. 3.1.5). Величина t называется параметром⁴, что дает основание называть равенства (3.1.5) парамет-рическими уравнениями плоской кривой.

Если из уравнений (3.1.5) удастся исключить параметр t, то приходим к уравнению плоской кривой в неявном виде

F(x, y) = 0, (3.1.6)

которое, в свою очередь, в некоторых случаях можно разрешить относительно y:

y = f (x). (3.1.7)

Таким образом, выражение (3.1.5) – (3.1.7) – различные формы записи уравнения плоской кривой.

Например, установим, какая кривая задана следующими параметриче­скими уравнениями:

Исключая параметр t, получим уравнение

которое соответствует эллипсу. Уравнение эллипса можно привести к виду (3.1.6) или (3.1.7):

При п = 3 отображение (3.1.4) имеет вид

(3.1.8)

Равенства (3.1.8) представляют собой параметрические уравнения пространственной кривой. В механике с уравнениями (3.1.8) ассоциируется образ движущейся в пространстве точки.

В качестве второго примера составим параметрические уравне-ния винтовой линии, представ-ляющей собой траекторию движе-ния точки, проекция которой на плоскость Oxy совершает равномер-ное вращательное движение по окружности радиуса r c центром в точке О, а проекция на ось z перемещается равномерно со скоростью v.

Используя рис. 3.1.6, получаем параметрические уравнения винтовой линии

Нетрудно убедиться, что величина h = 2v выражает шаг винтовой линии.