
- •Задание для самостоятельного решения
- •2.35.3. Приведение общего уравнения поверхностей второго порядка
- •Глава третья. Введение в математический анализ
- •Основные виды отображений.
- •3.1.1. Числовая функция одной переменной.
- •Задание для самостоятельного решения
- •3.1.2. Числовая функция нескольких переменных.
- •3.1.3. Вектор-функция скалярного аргумента.
- •Задание для самостоятельного решения
- •Постройте кривые:
- •3.1.4. Последовательность. Числовая последовательность.
- •Задание для самостоятельного решения
- •3.2. Понятие о метрическом и нормированном пространствах.
- •Задание для самостоятельного решения
- •3.3. Ограниченные, открытые, замкнутые множества. Верхняя и нижняя грани числовых множеств. Диаметр множества.
- •Задание для самостоятельного решения
- •3.4. Предел последовательности в метрическом пространстве.
- •Задание для самостоятельного решения
- •3.5. Предел отображения.
- •3.5.1. Предел числовой функции одной переменной.
- •Задание для самостоятельного решения
- •3.5.2. Предел числовой функции нескольких переменных
- •3.6. Бесконечно малые, ограниченные, бесконечно большие и отделимые от нуля величины
- •3.7. Простейшие свойства бесконечно малых величин
- •3.8. Простейшие свойства пределов.
- •3.9. Сравнение бесконечно малых.
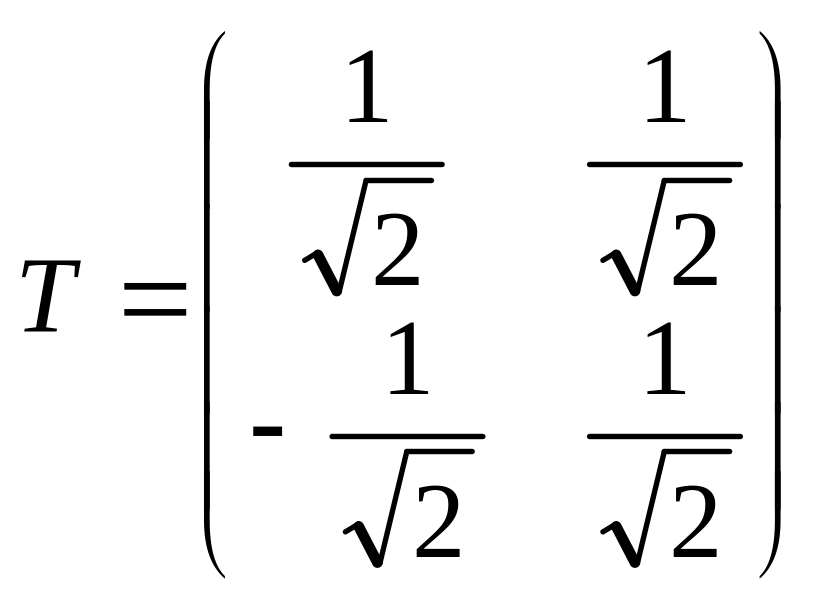 .
.
Напомним, что
![]() является ортогональной матрицей.
является ортогональной матрицей.
Преобразуем с помощью матрицы линейную форму данного уравнения по схеме
![]()
где
![]()

Таким образом,
![]()
В новой системе координат вместо исходного уравнения получаем
![]()
И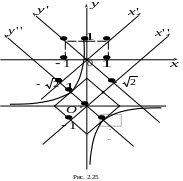 збавимся
от линейной формы путем выделения
«полных квадратов»:
збавимся
от линейной формы путем выделения
«полных квадратов»:
![]()
![]()
– уравнение гиперболы.
Здесь обозначено
![]()
Итак, в системе координат
![]() уравнение кривой принимает канонический
вид
уравнение кривой принимает канонический
вид
![]()
![]()
Оси координат
системы
параллельны осям координат
![]() и
и
![]() соответственно, а начало «передвинуто»
в точку
соответственно, а начало «передвинуто»
в точку
![]() (рис.2.25).
(рис.2.25).
Задание для самостоятельного решения
Какой вид примет уравнение (2.35.9) при
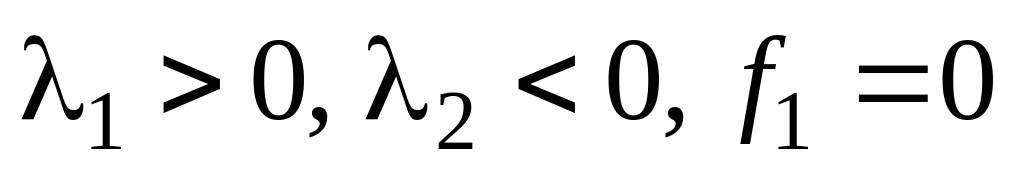 ?
Результат изобразите графически.
?
Результат изобразите графически.Запишите уравнение эллипса с центром в точке
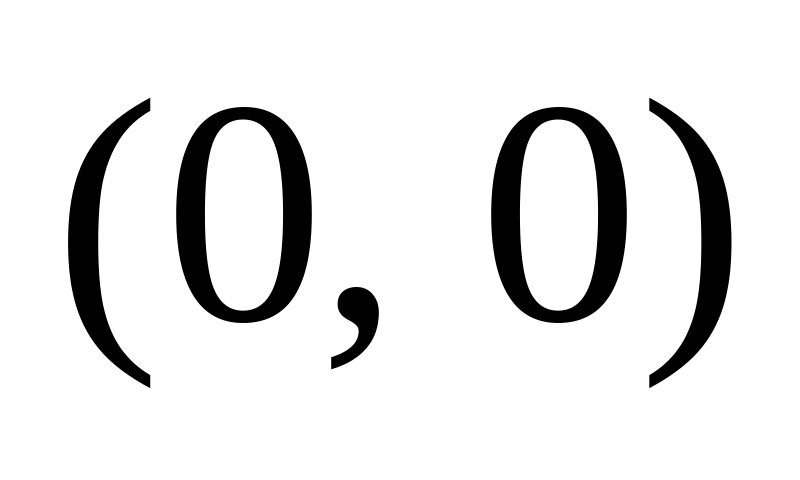 ,
если его полуоси равны 2 и 5.
,
если его полуоси равны 2 и 5.З
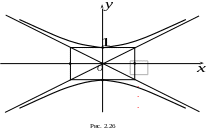 апишите
уравнение гиперболы, изображенной на
рис. 2.26.
апишите
уравнение гиперболы, изображенной на
рис. 2.26.
4. Запишите
уравнение биссектрисы угла
![]() ,
где
,
где
![]() ,
а
,
а
![]() фокусы эллипса
фокусы эллипса
![]()
У к а з а н и е: используйте свойство
нормали к эллипсу в точке
![]() (она является биссектрисой угла между
векторами
(она является биссектрисой угла между
векторами
![]() и
и
![]() ).
).
Запишите уравнение прямой, проходящей через точку
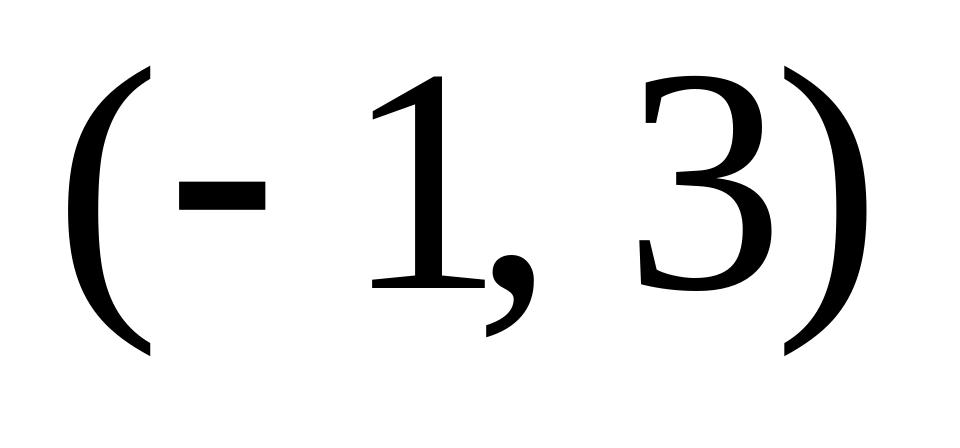 и центр окружности
и центр окружности
![]()
Найдите точки пересечения параболы
 с биссектрисой первой четверти.
с биссектрисой первой четверти.Запишите уравнение касательной к параболе
 параллельной прямой
параллельной прямой
 ;
перпендикулярной прямой
;
перпендикулярной прямой
 .
.Постройте кривые:
 6)
6)
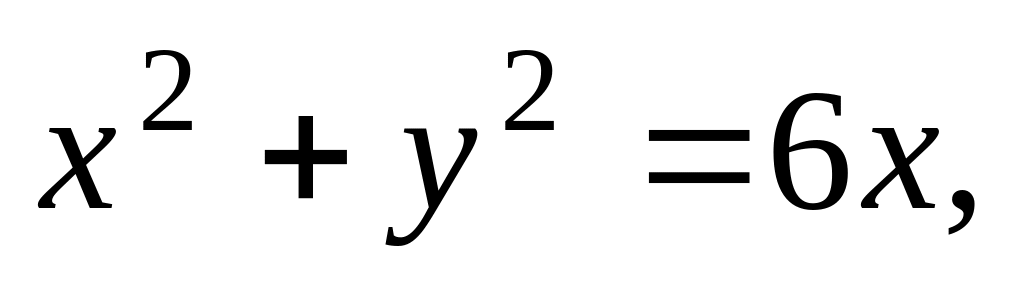
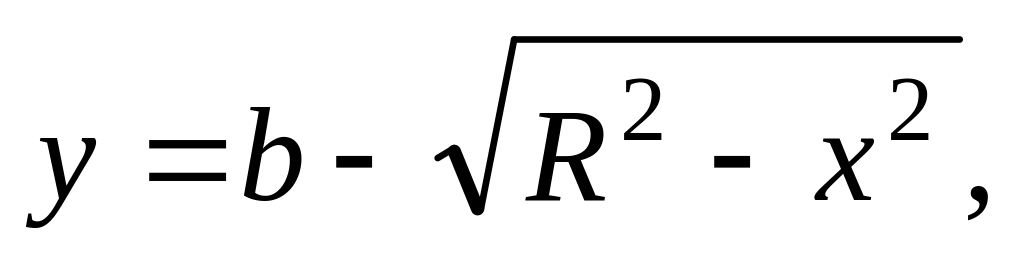 7)
7)
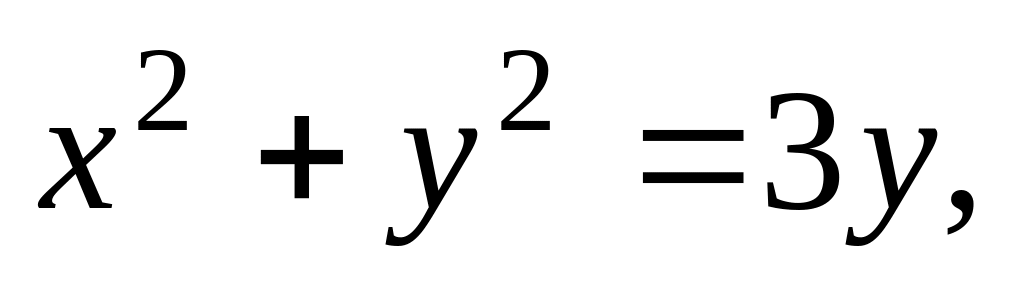
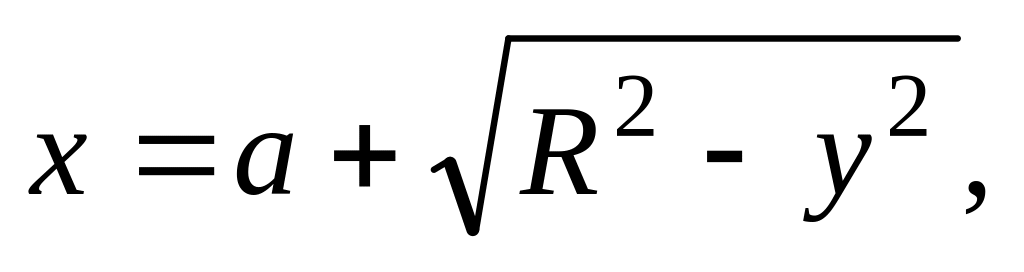 8)
8)
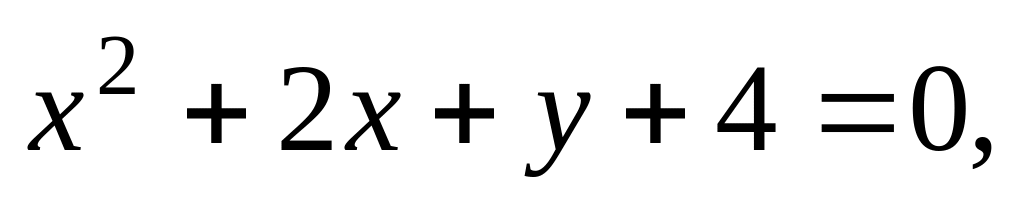
 9)
9)
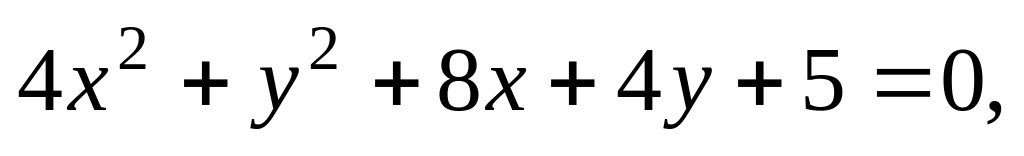
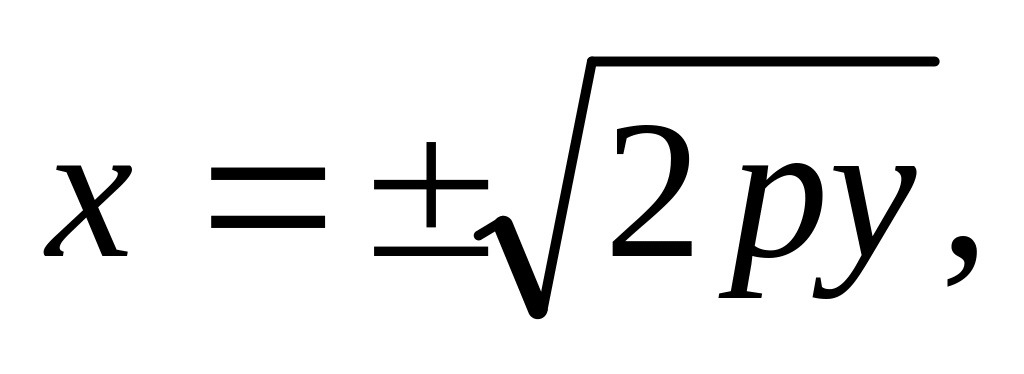 10)
10)
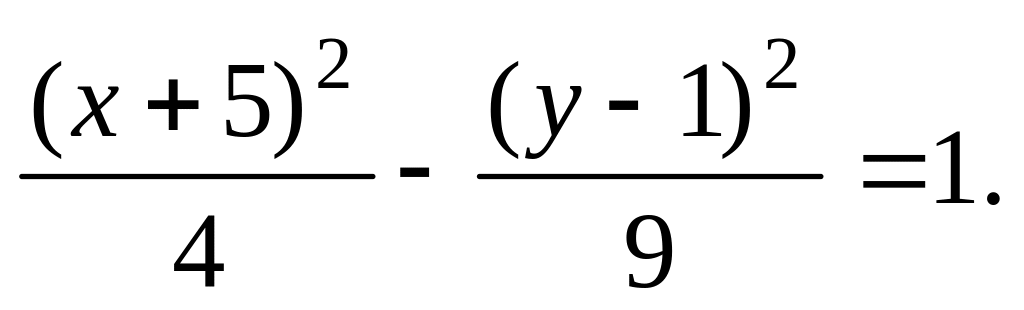
Приведите к каноническому виду уравнения кривых:
1)
![]()
2)
![]()
2.35.3. Приведение общего уравнения поверхностей второго порядка
к каноническому виду
Исследование общего уравнения поверхности второго порядка
![]() (2.35.14)
(2.35.14)
проводится по той же схеме, что и исследование уравнения кривой второго порядка. Естественно, различных геометрических образов здесь будет больше.
Итак, выполнив поворот системы координат так, чтобы направления новых осей совпали с направлениями собственных векторов матрицы
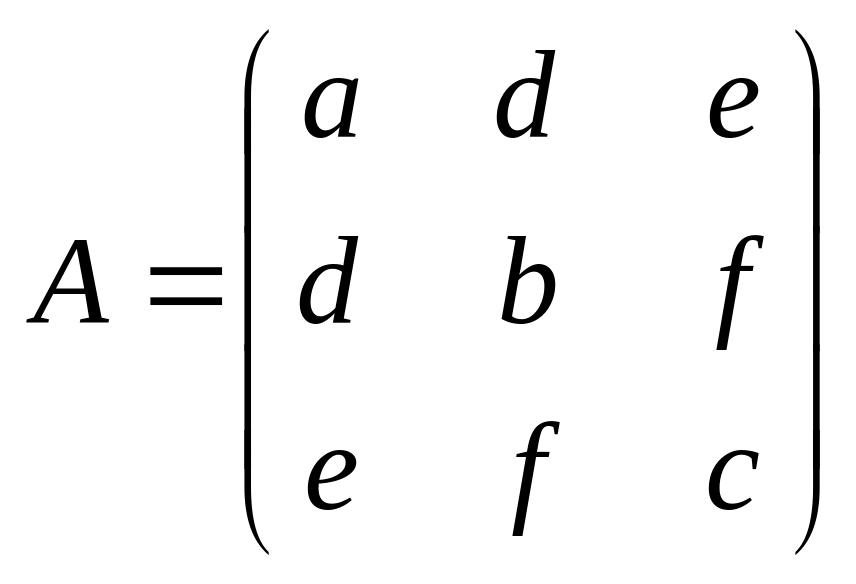
квадратичной
формы
![]() ,
получим вместо (2.35.14) более простое
уравнение:
,
получим вместо (2.35.14) более простое
уравнение:
![]() (2.35.15)
(2.35.15)
где
![]()
собственные значения матрицы
собственные значения матрицы
![]() .
.
Глава третья. Введение в математический анализ
Возникновение математического анализа (т.е. дифференциального и интегрального исчислений) явилось переломным моментом как в истории математики, так и в истории всей человеческой культуры.
Созерцательно-статический характер жизни древних, не знавших сложных механизмов и не подвергавших глубокому анализу физических явлений окружающего мира, породил метафизическую математику, рассматривавшую лишь «застывшие» состояния и якобы в совершенстве копирующую гармонию мира. Едва ли не единственным исключением был Архимед, в трудах которого математика успешно сочеталась с проблемами физики и механики.
«Предтечей» высшей математики по праву считается Рене Декарт (1596-1650), провозгласивший познаваемость мира, изучение которого он считал основной задачей математики. Декарт и Пьер Ферма (1601-1665) независимо друг от друга разработали систему использования метода координат и алгебраических выкладок в геометрии. Ферма ввел кроме того и понятие дифференциала.
Создателями
высшей математики (математического
анализа) явились крупнейшие мыслители
XVII в. Исаак Ньютон
(1643-1727) и Готфрид Вильгельм Лейбниц
(1646-1716). Им принадлежит связное изложение
нового исчисления, алгоритм отыскания
производных и анализ связи между
производной и интегралом. Лейбницем, в
частности, были введены обозначения y
= f (x)
для функции и
![]() для её производной.
для её производной.
Интересно отметить, что Лейбниц первоначально называл интеграл суммой (S), а интегральное исчисление – сумматорным исчислением. Термины интеграл (от лат. integer – целый) и интегральное исчисление были предложены его учениками Якобом (1654-1705) и Иоганном (1667-1748) Бернулли – представителями уникального «математического» семейства, давшего в XVII – XVIII вв. восемь прекрасных математиков.
Ученики И. Бернулли – Франсуа Антуан де Лопиталь (1661-1704) и Леонард Эйлер (1707-1783), а затем Жан Лерон Даламбер (1717-1783), Жозеф Луи Лагранж (1736-1813) и его ученик Жан Батист Фурье (1768-1830), Огюстен Луи Коши (1789-1857) и Георг Фридрих Бернхард Риман (1826-1866) и другие выдающиеся учёные – математики не только сыграли огромную роль в дальнейшем прогрессе математики, физики и механики, но и создали мощный аппарат, приспособленный для анализа всевозможных процессов и явлений природы, позволивший далеко раздвинуть рамки познания окружающего мира и вселенной.
Сегодня понятия производной и интеграла стали необходимыми элементами общей культуры человека. Они расширяют кругозор и оказываются полезными не только при решении технических задач, но и в самых разных областях знаний.
