2. Cистема с конечным накопителем: m/m/1:n

Рассмотрим СМО, для которой фиксировано максимальное число ожидающих заявок. Предположим, что в системе может находиться Nзаявок, включая находящуюся на обслуживании в сервере. Любое поступившее сверх этого числа требование получает отказ и немедленно покидает систему. В телефонии такие вызовы называют потерянными. Поступающие заявки образуют Пуассоновский поток, а обслуживание осуществляется одним сервером с показательным законом распределения времени обработки. Приспособим для описания такой системы модель процесса гибели-размножения.

Эта система эргодична и диаграмма интенсивностей переходов может быть изображена так как на рис. 1.15.

Рис. 1.15 Диаграмма интенсивностей переходов системы типа М/М/1:N.

Найдем распределение вероятностей в стационарном режиме непосредственно из общей формулы

Найдем теперь начальную вероятность, следуя общей формуле:

Таким образом, окончательная формула для стационарных вероятностей будет:

Проанализируем характеристики качества обслуживания (QoS) для такой системы. Важнейшей характеристикой будет являться вероятность блокировки – потери заявки. Очевидно, что это произойдет с вероятностью переполнения буфера, поэтому для расчета вероятности блокировки можно использовать формулу:

.

Например, для системы с коэффициентом использования 0.5 при размере буфера N=18 вероятность блокировки будет больше 10^-6, а при размереN=19, меньше этого значения. Следовательно, для получения вероятности блокировки такой величины необходимо предусмотреть размер буфера не менее 19.

Средняя длина очереди в буфере может быть найдена как:

.

Соответственно задержка может быть найдена на основе формулы Литтла

.

Определим пропускную способность системы как число заявок, обслуживаемых системой в одну секунду. Очевидно, что при вероятности блокировки P_Bпропускная способность может быть найдена как чистая интенсивность поступлений, то есть:

.

С точки зрения выхода системы пропускная способность может быть определена иначе. Если система всегда была бы непуста, то ее производительность равнялась бы величине обратной среднему времени обслуживания, то есть μ.Однако, поскольку часть времени система может простаивать, вероятность того, что в ней нет ни одной заявки отлична от нуля, реальная производительность может быть выражена как:

.

Подставив выражения для вероятности простоя сервера для системы с бесконечным размером буфера, получим:

.

Для системы с конечным буфером получаем:

.

В качестве реального примера рассмотрим концентратор сети с коммутацией пакетов, который обрабатывает пакеты со средней длиной 1200 бит. При скорости передачи в канале 2400 бит/с средняя пропускная способность его составит μ=2 пакета/с. Если полный входной поток имеет интенсивностьλ =1 пакет/с, тоρ =0.5 и можно рассчитать, что при размере буфера N =9 пакетов в среднем по 1200 бит, вероятность блокировки составит 0.001. Для того, чтобы получить вероятность блокировки 0.000 001 нужно предусмотреть буфер длиной не менее 19 пакетов по 1200 бит, т.е. около 2850 байт.

3. Система с несколькими серверами: m/m/m

Рассмотрим сначала простой случай системы, содержащей два сервера, любой из которых доступен для поступающих на вход заявок. Системы с несколькими серверами такого типа называют полнодоступными. Очевидно, что по сравнению с односерверной системой производительность будет выше. Сразу отметим, что интерес будет представлять сравнение с односерверной системой интенсивность обслуживания в которой в среднем вдвое выше, то есть мы ответим на вопрос что эффективнее удвоение скорости обработки или распараллеливание обработки.

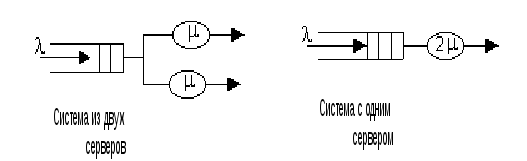
Система M/M/2может быть представлена как процесс размножения-гибели с параметрами:

Найдем сначала распределение вероятностей в стационарном режиме:

Находя из условий нормировки вероятность простоя (нулевого состояния), находим

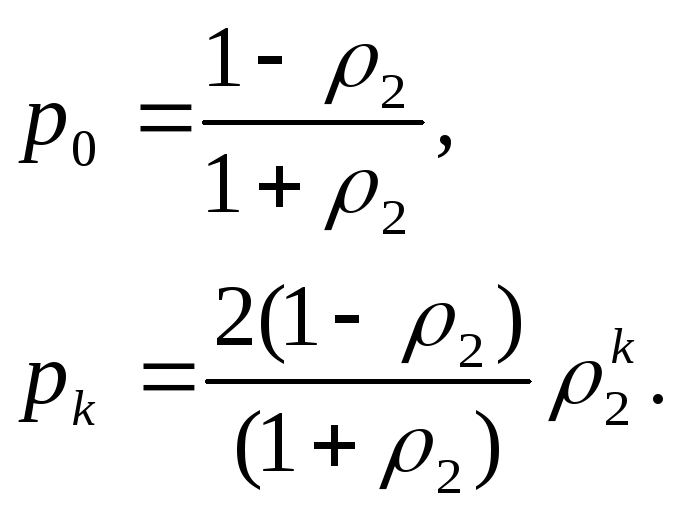
Найдем теперь основные характеристики качества обслуживания. Средняя длина очереди составит:

.

Теперь найдем среднее время задержки в системе по формуле Литтла:

.

Таким образом, в системе с двумя серверами время задержки сокращается. Нетрудно убедиться, что производительность системы M/M/2 также выше, поскольку теперь средняя производительность будет определяться вероятностью занятости только одного сервера и незанятости обоих серверов:

.

Получилось, что производительность системы без блокировки также как и для системы с одним сервером совпадает с входной нагрузкой, тогда как максимальная производительность могла равняться 2μ.

Найдем теперь для сравнения характеристики качества обслуживания для односерверной системы с вдвое большей пропускной способностью сервера μ. Воспользуемся формулами для системы M/M/1.

На рис. 1.16 представлены нормированные графики среднего времени задержки в системе с одним и с двумя серверами одной и той же производительности и с одним серверов, работающим с вдвое большей скоростью. Как видно из сравнения, увеличение вдвое скорости работы сервера оказывается более эффективным, чем введение параллельного сервера той же производительности.

Рис. 1.16 Нормированные графики среднего времени задержки в системе с одним и с двумя серверами одной и той же производительности и с одним серверов, работающим с вдвое большей скоростью.

Рассмотрим теперь общий случай СМО с mсерверами. Диаграмма интенсивностей переходов для такой системы представлена на рис. 1.17.

Р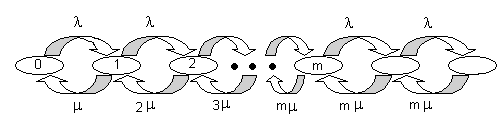исунок 1.17. Диаграмма интенсивностей переходов для СМО типа M/M/m.

Интенсивности переходов могут быть определены следующим образом:

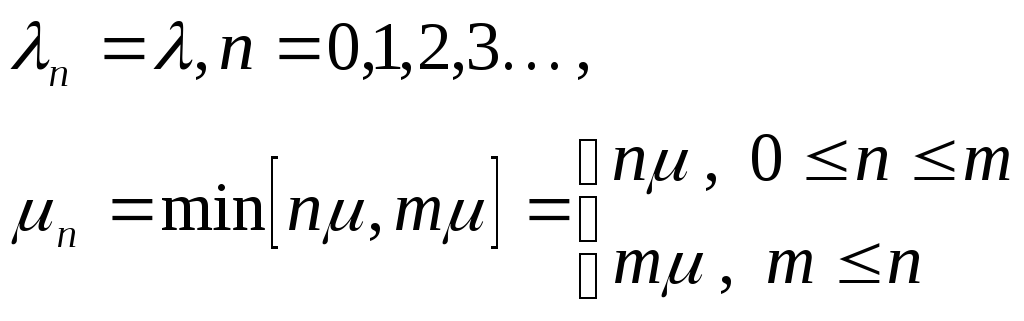
Используя основные общие соотношения для процессов гибели-размножения, получим:

Вероятность простоя определяется громоздкой формулой, которая может быть записана через общую входную нагрузку Аи удельную нагрузкуна один сервер:

.

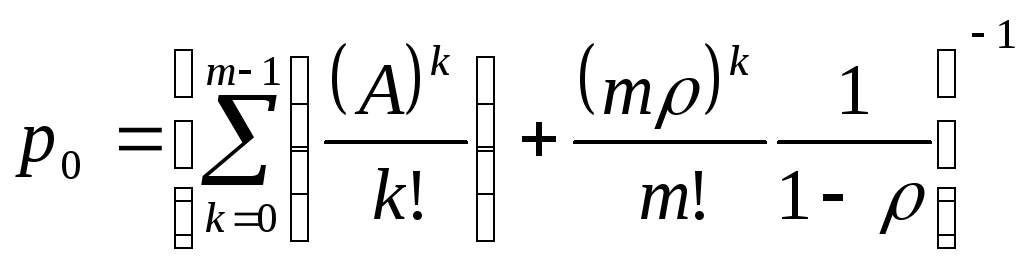Полученные здесь соотношения позволяют рассчитать все характеристики QoS, мы приведем только одну формулу, позволяющую найти вероятность того, что поступающее в систему заявка окажется в очереди. Эту формулу широко используют в телефонии: она определяет вероятность того, что поступающий на пучок из mлиний вызов, не застанет ни одной свободной линии и будет поставлен в очередь на обслуживание. Эту формулу часто называютС-формулой Эрланга.

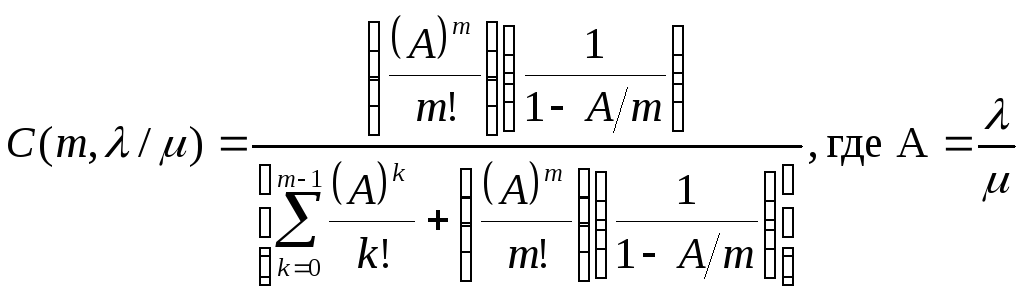
Модель СМО, описываемая С - формулой Эрланга называется также LostCallsDelayed(LCD).