
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального
образования
Уфимский государственный авиационный технический университет
Кафедра ТС
Курсовая работа по дисциплине
“Теория электрической связи”
Расчет системы передачи дискретных сообщений
Вариант 8
Выполнила:
ст. гр. СПР-310
Денисова Ю.А
Проверил:
Салихов А. И
Уфа 2007
Содержание
Содержание 1
Задание на курсовую работу: 2
1. Источник сообщений. 3
3. Кодер. 8
4. Модулятор. 12
5. Канал связи 16
6. Демодулятор 18
7. Декодер 21
8. Фильтр – восстановитель 23
Задание на курсовую работу:
Рассчитать основные характеристики системы передачи сообщений, структурная схема которой имеет следующий вид:
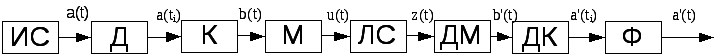
ИС – источник сообщения;
Д – дискретизатор;
К – кодер;
ЛС – линия связи;
ДМ – демодулятор;
ДК – декодер;
Ф – фильтр-восстановитель.
Исходные данные:
amin = -1,6 B;
amax = 1,6 B;
Fc = 15*103 Гц;
j = 9;
Вид модуляции ЧМ;
N0 = 2,9∙10-7 B2/Гц;
Способ приема когерентный.
1. Источник сообщений.
Источник сообщений выдает сообщение a(t), представляющее собой непрерывный стационарный случайный процесс, мгновенные значения которого в интервале [amin; amax] распределены по заданному закону, а мощность сосредоточена в полосе частот от 0 до Fc.
Требуется:
1) Записать аналитическое выражение и построить график одномерной плотности вероятности мгновенных значений сообщения a(t).
2) Найти математическое ожидание, дисперсию и СКО.
3) Построить график случайного процесса и на графике обозначить максимальное и минимальное значения сигнала, математическое ожидание и среднеквадратичное отклонение.
Решение:
1.1.![]()
![]() -площадь
равнобедренной трапеции.
-площадь
равнобедренной трапеции.
Из
условия нормировки
![]()
![]() .
.![]()
![]() ,
,
Н=0.4167.
Одномерная плотность вероятности мгновенных значений сообщения a(t) описывается системой вида:
P(a)=
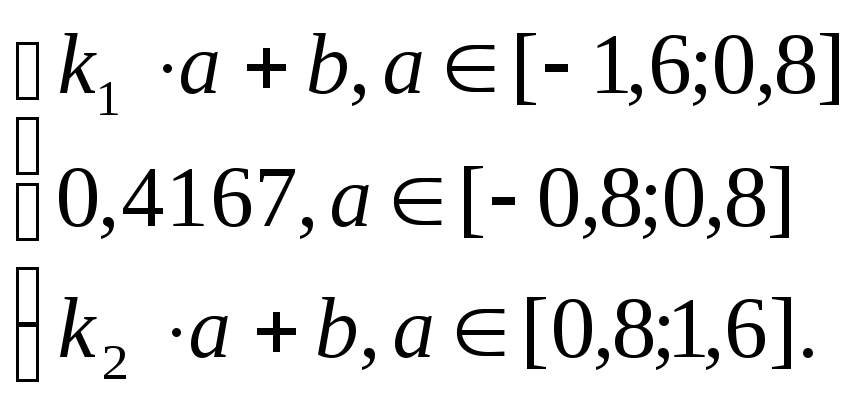
Для P(a)= K1*a+b по графику берем две точки (a;p(a)): (-1,6;0) и (-0,8;0,4167).
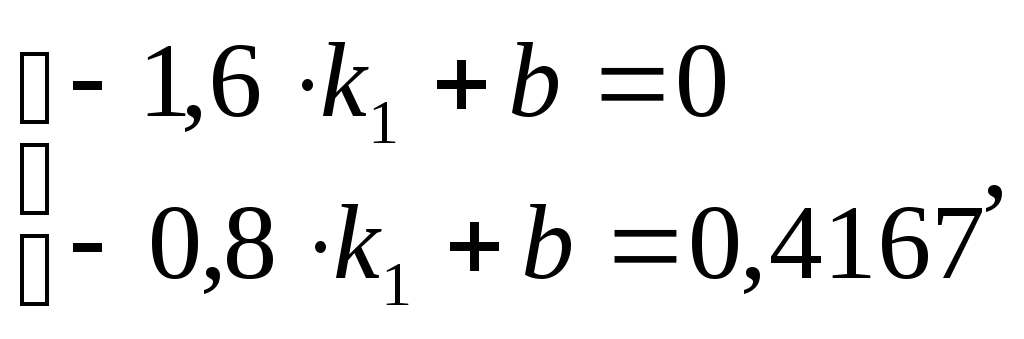 из
системы уравнений находим k1
и b
:
из
системы уравнений находим k1
и b
:
![]()
![]() ;
;![]() .
.
В результате получаем Р(а)=0,52*a+0.8334.
Аналогично, находим Р(а)= k2*a+b=-0,52*а+0,8334, т.к. трапеция – равнобедренная, k2=-k1. В результате получим:
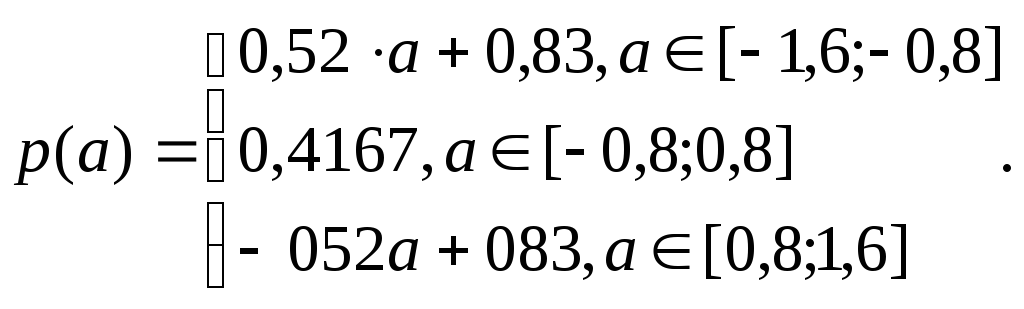
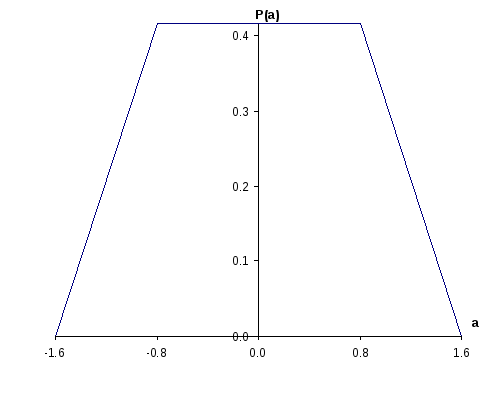
Рис.1.1.Распределение одномерной плотности вероятности
1.2. Найдем математическое ожидание:
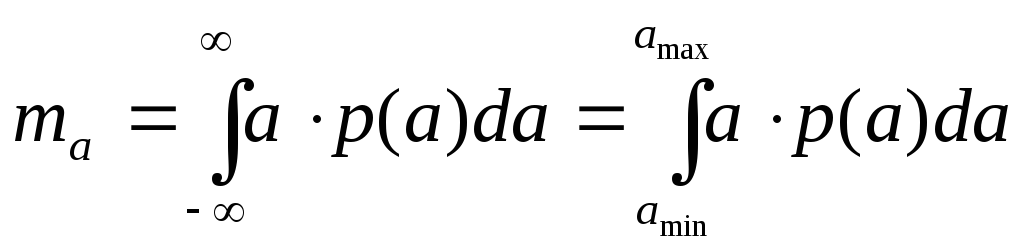 .
.

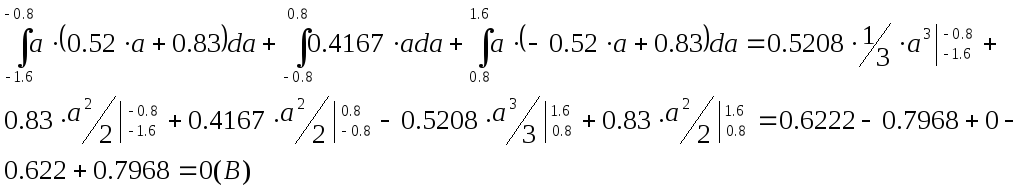
Найдем дисперсию:
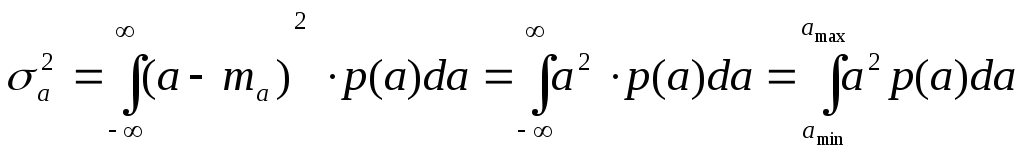

Найдем СКО:
![]() .
.
0 < 0,6442 < 1,6
1.3.
а, В
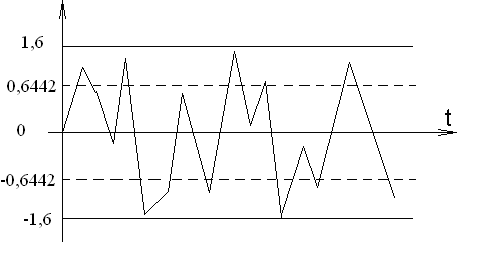
Рис.1.2. График случайного процесса а(t)
2. Дискретизатор.
Передача непрерывного процесса осуществляется дискретными методами. Для этого сообщение а(t) дискретизируется по времени и квантуется по уровню с равномерным шагом. Шаг квантования по уровню а= 0,1В.
Требуется:
Определить шаг дискретизации по времени (t).
Определить число уровней квантования (L).
Рассчитать среднюю мощность шума квантования.
4) Рассматривая дискретизатор как источник дискретного сообщения с объемом алфавита L, определить его энтропию и производительность (Н, Н’). Отсчеты, взятые через интервал t считать независимыми.
Решение:
2.1. . Найдем шаг
дискретизации по времени. Для этого
воспользуемся теоремой Котельникова
![]() ,
тогдаiаг дискретизации
по времени:
,
тогдаiаг дискретизации
по времени:
![]() ,
,
![]()
![]() ≈33,3мкс.
≈33,3мкс.
2.2. Число уровней квантования L при равномерном шаге определяется как частное от деления размаха сигнала на шаг квантования а. Т.к. шаг квантования по уровнюа задан, то число уровней квантования:
![]()
![]()
L=32.
2.3.Шум квантования представляет собой стационарный случайный процесс с независимыми значениями отдельных отсчетов = aд – a (эпсилон). Если в качестве квантованного значения a принимается ближайший дискретный уровень, то шум квантования (ошибка дискретизатора, возникающая из-за того, что не происходит переход на другой уровень) при равномерном квантовании с шагом a находится в пределах
![]()
![]() ,
,
здесь – шум квантования.
Поскольку квантование по уровню ведется с равномерным шагом,то закон распределения плотности вероятности шума квантования ωш(ε) также будет равномерным и не будет зависеть от номера интервала квантования:
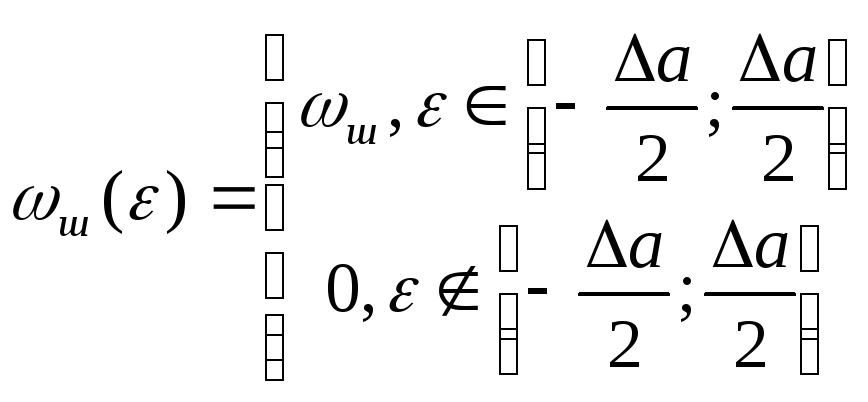 , где ωш= 1/Δa.
, где ωш= 1/Δa.
Найдем среднюю мощность (дисперсия шума квантования):
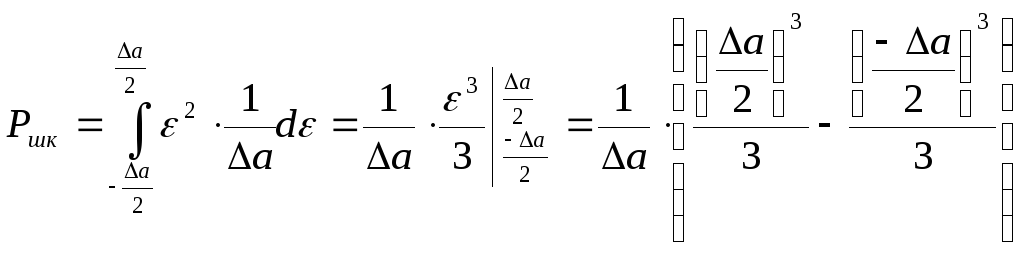 ,
,
Pшk![]() .
.
2.4.![]() Энтропия – средняя информативность
источника на один символ, определяющая
неожиданность выдаваемых сообщений
для источника без памяти энтропия
определяется по формуле:
Энтропия – средняя информативность
источника на один символ, определяющая
неожиданность выдаваемых сообщений
для источника без памяти энтропия
определяется по формуле:
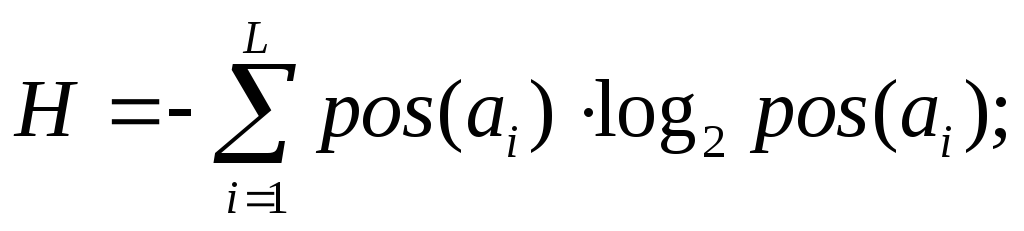
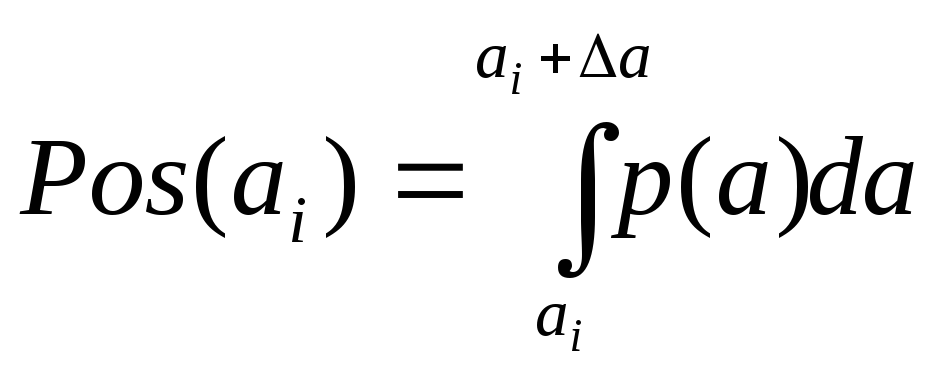 ,гдеi=1…n
,гдеi=1…n
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Определим вероятность на интервале [-0,8;0,8]:
![]()
![]() ,
,
![]()
![]()
![]() .
.
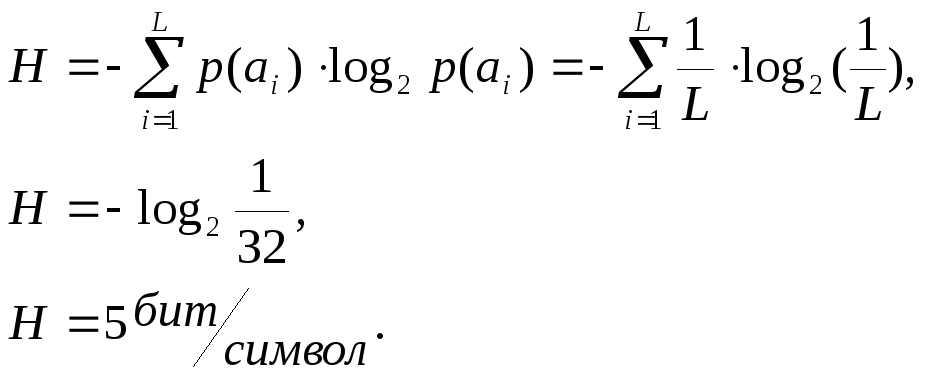
Определим производительность источника, как энтропию в единицу времени:
![]() .
.
