3. Анализ систем массового обслуживания с марковскими потоками требований.

В этом разделе вы познакомитесь с методами расчета характеристик качества обслуживания QоS систем массового обслуживания, если они могут быть описаны моделью с марковским потоком требований на входе, т.е. интервалы времени между поступлениями соседних требований являются случайной величиной с экспоненциальным распределением.

1. Система м/m/1. Анализ.

Как было описано при классификации систем, это система с пуассоновским входным потоком заявок, экспоненциальным законом распределения времени обслуживания и одним сервером.

На рис. 1.10 приведена простейшая схема такой системы. Она содержит буфер, который может хранить очередь бесконечной длины, состояние которой может быть отождествлено с числом заявок, содержащихся в очереди в каждый момент времени.

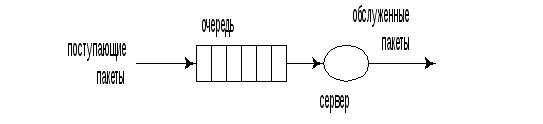
Рис. 1.10 СМО типа М/М/1.

Поскольку входной процесс ординарный, то в каждый момент времени к очереди может добавиться только одна заявка, поскольку сервер один, то в каждый момент времени может быть обслужена, то есть уйти из очереди только одна заявка. Таким образом, рассматриваемая СМО относится к процессу класса «гибели-размножения». Для анализа необходимо конкретизировать параметры системы. Распределение вероятностей входного потока и времени обслуживания позволяет полагать интенсивности вероятностей в модели постоянными.

Здесь – среднее время обслуживания в сервере.

На рис 1.11 приведена диаграмма интенсивностей переходов для рассматриваемой системы.

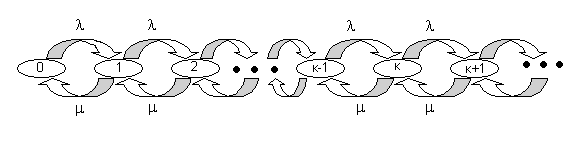
Рис. 1.11 Диаграмма интенсивности переходов для СМО типа М/М/1.

Полученное ранее общее решение позволяет сразу записать вероятность того, что в стационарном состоянии в очереди будет находиться kзаявок

Найдем начальное значение вероятности, учитывая сходимость соответствующего ряда

.

Окончательно получаем формулу для вероятности длины очереди

.

На рис. 1.12 приведен график вероятностей того, что в очереди находится kзаявок в установившемся режиме.

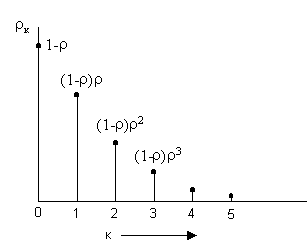
Рис. 1.12 Стационарные вероятности р_кдля СМО типа М/М/1.

Теперь найдем наиболее интересные характеристики.

Важной характеристикой системы является средняя длина очереди. Зная вероятности каждого из возможных значений длины, найдем математическое ожидание:

.

График средней длины очереди заявок в системе в зависимости от значения коэффициента использования или нагрузки показан на рис. 1.13.

Найдем теперь дисперсию длины очереди:.

Для нахождения среднего значения времени пребывания в очереди воспользуемся формулой Литтла.

.

На рис. 1.14 приведен график зависимости среднего времени пребывания в очереди в зависимости от коэффициента использования (нагрузки).

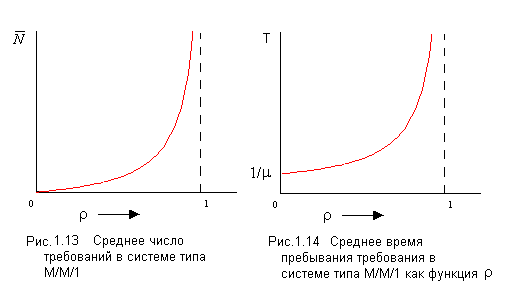
Рассматривая полученные результаты, нетрудно видеть, что при увеличении коэффициента использования, как длина очереди, так и время пребывания в ней неограниченно возрастают при приближении ρк единице. Такой вид зависимости от коэффициента использования характерен для почти всех СМО.

Наконец найдем вероятность того, что в очереди будет находиться не менее чем kзаявок и того, что в очереди менееkзаявок.

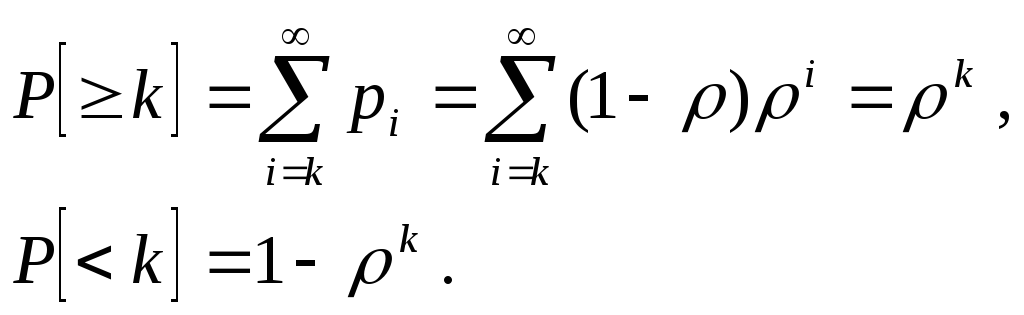
Итак, в ходе анализа простей шей системы М/М/1 нам удалось в аналитическом виде найти все практически интересные характеристики Q_oSсистемы.