4. Система обслуживания с m серверами и с явными потерями: m/m/m:Loss

Предметом рассмотрения теперь будет система без образования очереди для заявок, поступивших в моменты, когда все mсерверов были заняты. Такие заявки будут просто теряться. В телефонии это типичный случай коммутирования на конечном коммутационном поле. Опишем такую систему подходящим процессом типа гибели-размножения. Его параметры могут быть определены так

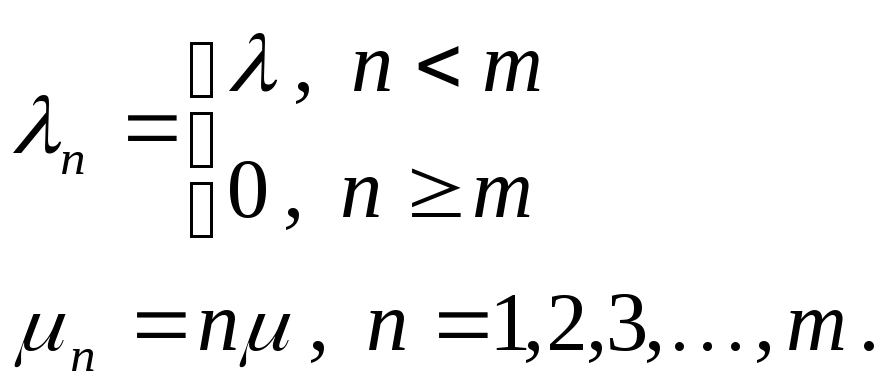
Такая система оказывается также эргодичной и диаграмма интенсивностей переходов, приведенная на рис. 1.18 позволяет найти распределение вероятностей:

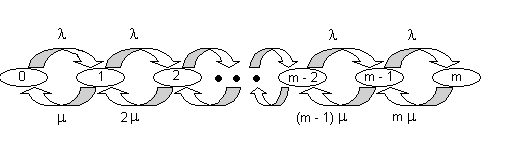
Рис. 1.18 Диаграмма интенсивностей переходов для СМО типа M/M/m:Loss.

Основной характеристикой QoS для этой системы является средняя доля времени, когда все серверы оказываются занятыми. В этом случае говорят о том, что в системе наступила блокировка. Вероятность такой блокировки определяется по формуле, носящей в телефонии название В - формулы Эрлангаили формулой потерь Эрланга

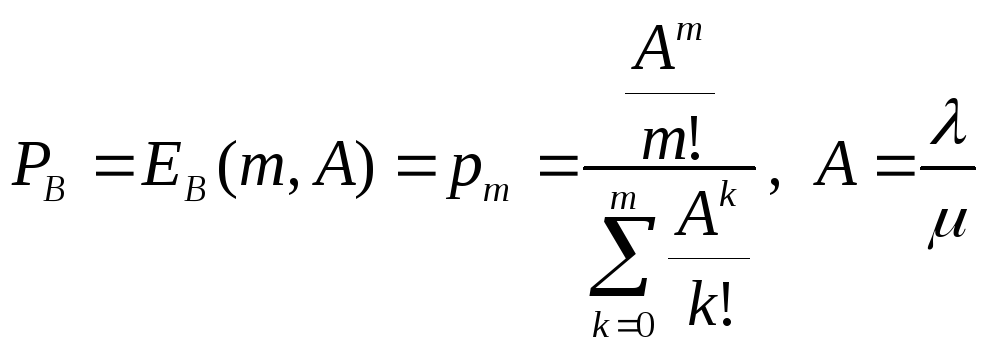
Эта формула играет столь большую роль в телефонии, что ее значения табулированы и существует масса таблиц, обратного расчета, то есть определения нагрузки, при которой обеспечивается заданная вероятность блокировки для заданного числа серверов. Такая таблица важна при расчетах многих сетей и систем массового обслуживания. Модель СМО, описываемая В - формулой Эрланга называется также LostCallsCleared(LCC).

5. Система обслуживания m/m/m:k/m конечное число источников нагрузки, m серверов и конечный накопитель.

О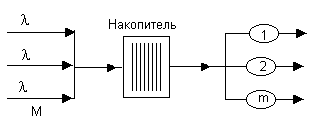сновной смысл изучения такой системы состоит в том, что входной поток в такой системе может рассматриваться как примитивный, то есть параметр потока зависит от числа требований, находящихся на обслуживании. Эта зависимость определяется таким образом, что изMисточников пуассоновского потока с постоянным параметромλполучают отказ те требования, которые поступают в систему тогда, когда в ней уже имеютсяKзаявок. Система описывается процессом типа гибели-размножения с диаграммой интенсивностей переходов на рис. 1.19.

Рис. 1.19 Диаграммой интенсивностей переходов для СМО типа M/M/m:K/М.

и параметрами интенсивностей:

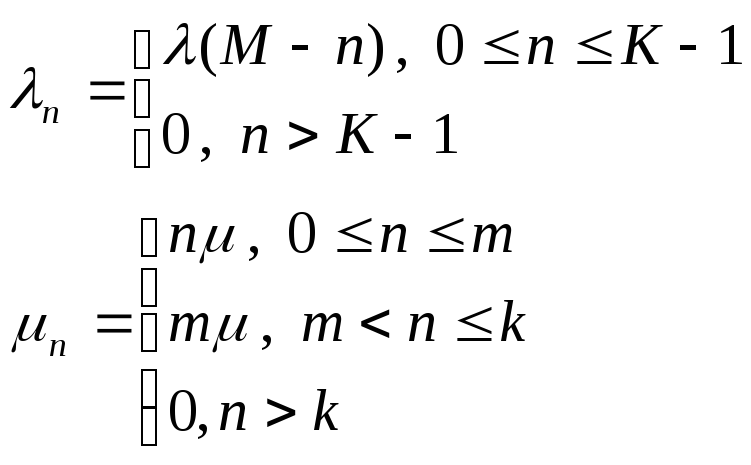
Воспользовавшись формулам для стационарных вероятностей, получим:

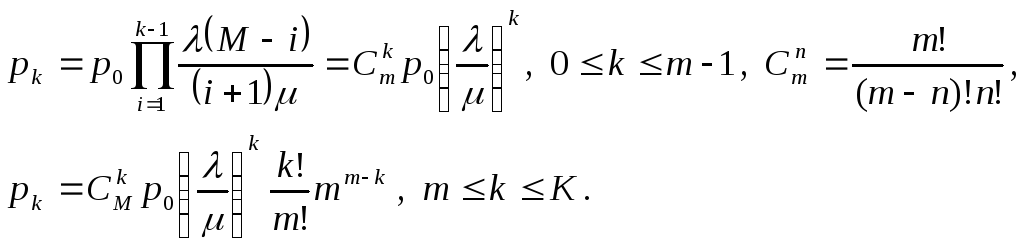
Формула для вероятности простоя очень громоздка и здесь не приводится. Если считать, что K = m, то есть в системе только чистые потери (длина буфера совпадает с числом серверов), то распределение стационарных вероятностей может быть дано в виде так называемогораспределения Энгсета:

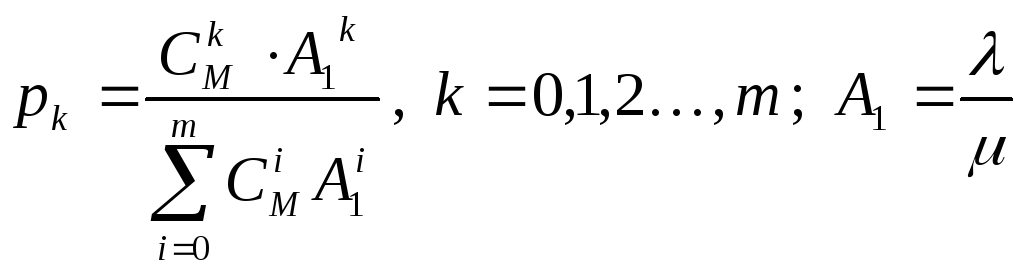
Эта формула имеет следующую интерпретацию.

Н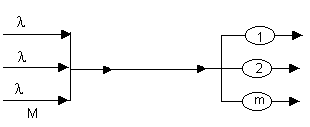екоторая система массового об­служивания, имеющаяМвходных линий, распределяет поступающие с них заявки наmсерверов. Интен­сивность входного потока зависит от того, сколько серверов занято об­служиванием таким образом, что интенсивность входного потока ли­нейно убывает с числом занятых серверов :.

Максимальная нагрузка, поступающая на один вход, определяется как:.

Вероятность того, что при показательном законе распределения времени обслуживания в стационарном режиме будет занято kсерверов, будет определяться как раз вышеприведенной формулой Энгсета. Систему такого типа можно назвать M/M/m:M. Полученное распределение также позволяет рассчитать вероятность того, что будут заняты все серверы. Для этого достаточно положитьk = m. Как видно, она отличается от полученной ранее формулы потерь Эрланга. Это распределение также часто встречается на практике и задается функцией Энгсета:

.

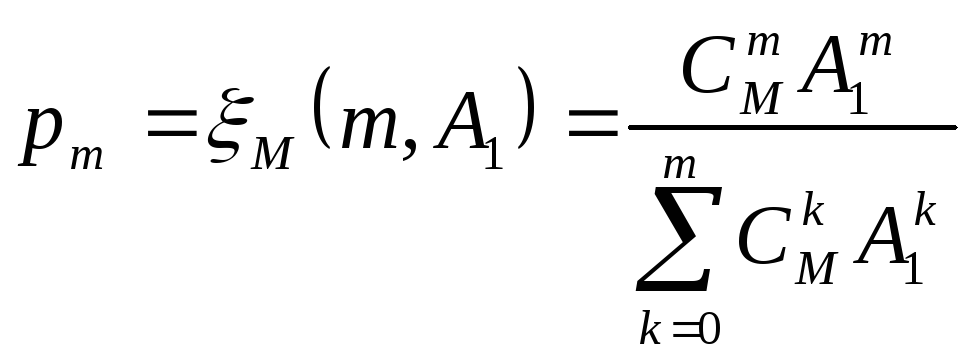На практике применима также модель Молина (Molina), которая также называется моделью потерянных вызовов (LCH – Lost Calls Held). Это математическая модель блокировки телефонного трафика, в которой блокированные обращения сохраняются в течение определенного времени задержки, хотя и не обслуживаются. Эта модель подобна модели, описываемой С – формулой Эрланга, с которой иногда и путается. Вероятность блокировки для N линий, создающих интенсивность А имеет вид:

.