Нестационарный пуассоновский поток.

Это ординарный поток без последействия, для которого в любой момент времени существует конечный параметр потока λ(t).ПустьP_i(t₀,τ)– вероятность поступленияi-требований за интервал [t₀,t₀+τ], которая определяется формулой:

, где.

Этот параметр имеет смысл среднего числа требований на промежутке [t₀,t₀+τ]. Средняя интенсивность определяется как:.

Выбором закона изменения λ(t)можно описать реальные потоки заявок на АТС (например, отразить наличие ЧНН).

Стационарный поток без последействия.

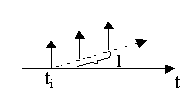
Это неординарный (групповой) пуассоновский поток. События–моменты вызовов, представляют собой простейший пуассоновский поток с параметромλ. В каждый момент времениt_i с вероятностьюp_lпоступает группа изl ( l =1,2,…r) одинаковых заявок. Величина l – характеристика неординарности. Обозначим параметрa_l =λp_l. Вероятность поступленияkтребований в промежутке времени длинойt:

.

Суммирование в этой формуле производится по всем j, удовлетворяющим соотношению :.

Это означает, что любой неординарный пуассоновский поток можно представить как kнезависимых неординарных пуассоновских потоков с постоянной характеристикой неординарностиl и соответствующими параметромa_l и интенсивностьюla_l. Параметр неординарного потока определяется как:,

а интенсивность такого потока : .

В качестве одного из примеров применения неординарного потока можно привести пуассоновский поток с неординарными заявками, т.е. использующим для своего обслуживания lсерверов. В сотовой системе связи в том случае, когда происходит звонок с мобильного телефона на телефоны не расположенные в зоне обслуживания одной базовой станции или на телефоны городской сети, требование обслуживается одним сервером – голосовым каналом, а при осуществлении звонка на мобильный телефон, обслуживаемый одной и той же базовой станцией требуется сразу два сервера – голосовых канала. Следовательно, поток вызовов от мобильных телефонов может рассматриваться как неординарный с характеристикой неординарности равной двум.

Примитивный поток.

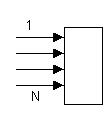
Это ординарный поток, параметр которого прямо пропорциона­лен числу свободных источников N_i =(N-i). ЗдесьN– общее число источников требований,i- число обслуживаемых в данный момент источников. Для примитивного потока параметр потока определяется какλ_i=αN_i=α(N-i) с некоторым коэффициентом α. Среднее значе­ние параметра примитивного потока:, гдеf_­i - вероятность того, что об­служиваетсяiисточников. Средняя интенсивность потока заявок от одногоисточника: .

Поток с повторными вызовами.

Он состоит из потока первичных запросов – пуассоновский поток и повторных запросов. Параметр общего потока равен сумме параметров первичных и повторных заявок и может быть описан как примитивный с параметром:

Здесь обозначено: i - число обслуживаемых источников,j - число источников, повторяющих запрос, α – интенсивность первичного источника,β– интенсивность источника повторного запроса. Еслиα≈ß, то потоки неразличимы. Во многих городских АТСß>>αи можно произвести сепарацию потоков заявок по среднему времени обслуживания.