228. Общие свойства решения системы линейных уравнений. (Ранг системы, базисные и свободные переменные, общее и частное решение, фундаментальная система решений).

Используя свойства линейных операций с матрицыми, нетрудно доказать, справедливость следующих утверждений.

1. Если и 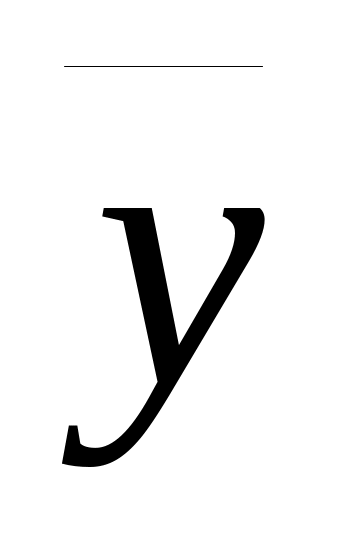— два решения системы 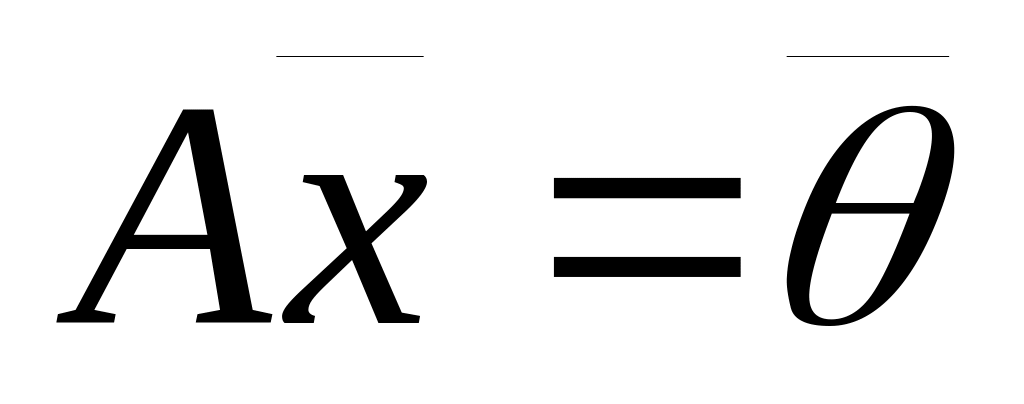, то при любых α и β вектор 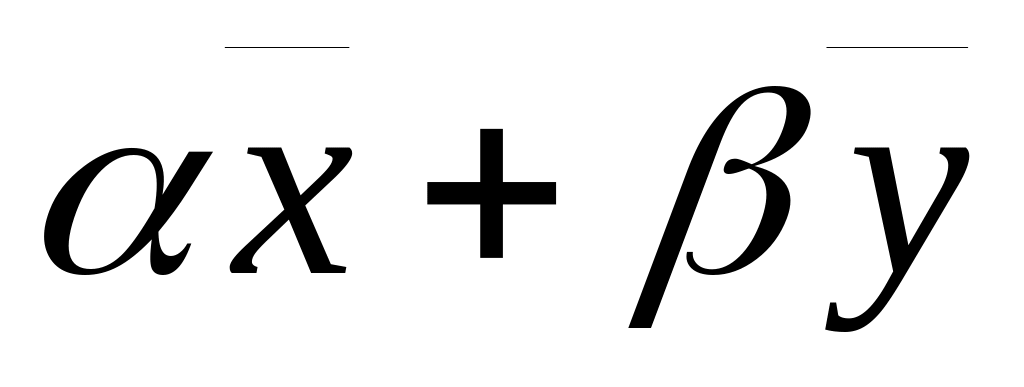— решение системы.

2. Если и — два решения системы , то вектор — решение приведенной однородной системы .

3. Если решение системы , а — решение системы , то вектор 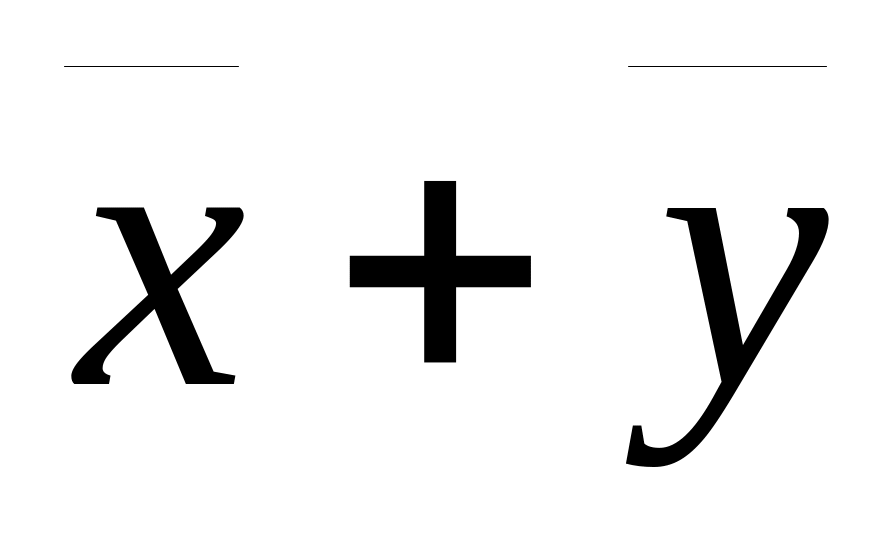— решение системы .

229. Определители Метод Гаусса решения систем линейных уравнений путем приведения их к

трапецеидальному виду.

(Система несовместна)

230. Определение и основные свойства матриц

Прямоугольная таблица m·n чисел, расположенных в m строках и n столбцах называется прямоугольной (m,n) матрицей или просто матрицей.

Числа m и n называются порядками или размерностями матрицы.

Если m=n, то матрица называется квадратной матрицей порядка m.

231. Cложение и Умножение матриц на число.

Суммой двух матриц одинаковой размерности называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых. .

Произведением матрицы на число называется матрица той же размерности, каждый элемент которой равен произведению соответствующего элемента на число:

.

Для операций сложения и умножения матрицы на число справедливо:

1. 1·A=A,

2. 0·A= 

3. α(βA) = (αβ)A,

4. A+(B+C) = (A+B)+C,

5. A+B = B+A,

6. (α+β)A=αA+βA,

7. α(A+B) = αA+αB.

где A, B, C — произвольные матрицы одинаковой размерности, — нулевая матрица той же размерности (читается «тэта»), и — произвольные числа.

232Матрицы Транспонирование матриц, строки и столбцы.

233Матрицы Линейная комбинация строк или столбцов.- зависимая и не зависимая.

234. Основные свойства умножения матриц и их произведения

Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй. Если

то произведением матриц A и B называется матрица

,

элементы которой вычисляются по формуле

, ;

произведение матриц A и B обозначается AB: C=AB.

Пример:

.

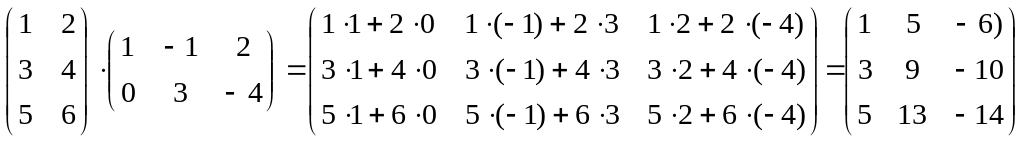Для произведения матриц соответствующих порядков справедливо:

1. A·B ≠ B·A,

2. (A + B) · C = A·C + B·C,

3. C·(A + B) = C·A + C·B,

4. α(A·B) = (αA) ·B,

5. (A·B) ·C = A·(B·C).

Если AB = BA, то матрицы A и B называются перестановочными.

Для квадратных матриц определена единичная матрица — квадратная матрица, все диагональные элементы которой единицы, а остальные — нули:

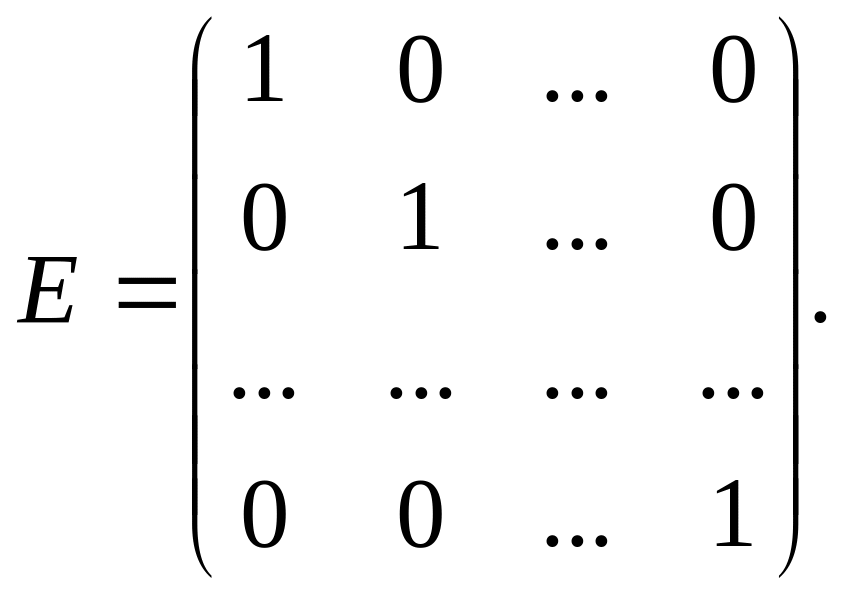
Единичная матрица чаще всего обозначается буквой E или E_n, где n —порядок матрицы. Непосредственным вычислением легко проверить основное свойство единичной матрицы AE=EA=A.

235. Основные свойства алгебраических операций над матрицами.

Для операций сложения и умножения матрицы на число справедливо:

1·A=A,

0·A= 

α(βA) = (αβ)A,

A+(B+C) = (A+B)+C,

A+B = B+A,

(α+β)A=αA+βA,

α(A+B) = αA+αB.

где A, B, C — произвольные матрицы одинаковой размерности, — нулевая матрица той же размерности (читается «тэта»), и — произвольные числа.