27. Определение координат точки.

Компоненты радиус-вектора называются координатами т. М в рассматриваемой системе координат, координаты т. определяются однозначно.

28. Предложение 1 о компонентах вектора.

Чтобы найти компоненты вектора нужно из координат конца вычесть координаты начала

М’М (х’-x, y’-y, z’-z)

29. Деление отрезка в заданном отношении.

Рассмотрим отрезок АВ .

Найдем координаты т.М ,которая делит АВ отрезок в отношении

=

= (1)

Обозначим через (x , y , z) координаты точки А, ( ) –т. В , ( ) –т. М

Разложим обе части равенства (1) по базису, тогда имеем 3 уравнения с 3 неизвестными

{ } - ?

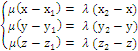формулы деления отрезка в заданном отношении:

Если одно из выражений будет отрицательным то точки М будет находится в не отрезка АВ.

Соответственно это будет деление отрезка АВ внешним образом.

30. Декартова прямоугольная система координат.

ДСК, которая имеет нормированный базис называется ДПСК.

31. Определение ортонормированного базиса.

Базис называется ортонормированным, если его векторы (ортогональны) , а по длине =1

, , → = = = 1

32. Полярная система координат.

Существует формула перехода

→

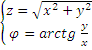
33. Цилиндрические и сферические координаты.

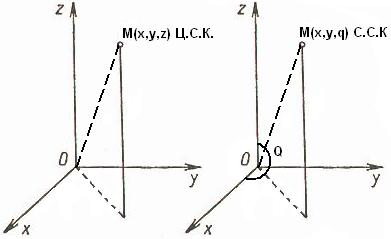
34-35. Определение Скалярного произведения и его свойства.

Скалярное произведение – число, равное произведению двух векторов на косинус угла между ними.

Свойства скалярного произведения:

1. Комунитативность:

2. - для любого вектора

3. , если или .

, если или или _┴ .

36. Предложение 1 о компонентах вектора в ортонормированном базисе.

Если базисные вектора ортогональны (_┴), то компоненты любого вектора находятся по формулам:

; ; .

37. Предложение 2 о линейности СП.

Свойство линейности СП для любых , , чисел и имеет вид:

Следствия:

38. Теорема 1 о представлении СП.

Если базис перпендикулярен, то скалярное произведение векторов вирируется:

Доказательство:

Пользуясь и ; ; , полученное будем последовательно перемножать (1^ую сумму на 2^ую).

Таким образом и получим выписанное выражение.

39. Таблица перемножения базисных векторов для СП.

	1	0	0
	0	1	0
	0	0	1

40. Выражение длины вектора.

Из теоремы о представлении СП позволяет написать выражение вектора через его координаты в ортогональном базисе:

41. Выражение угла между векторами.

Из теоремы о представлении СП следует выражение косинуса угла между векторами и через их компоненты:

42. Выражение расстояния между 2-мя точками.

Используя формулу для измерения величины вектора можно написать формулу для расстояния между двумя точками:

43. Ориентация тройки векторов (левая и правая).

Упорядоченная тройка некомпланарных векторов называется правоориентированной, если из конца вектора кратчайший поворот к вектору виден против часов стрелки, в противном случае – левоориентированна.

44. Векторное произведение (ВП). Определение.

Векторным произведением называется вектор , удовлетворяющий:

1.

2. _┴ и _┴

3. Если и не коллинеарны, то векторы , и образуют кривую тройку векторов.

45. Предложение 3 об антикоммукативности ВП.

Т.к. в формулу ВП входит синус угла, то ВП непереставляемо (антикомунитативно).

46. Таблица перемножения базисных векторов для ВП.

	0		-
	-	0
		-	0

47. Смешанное произведение (СмП) Определение.

Смешанное произведение 3^ёх некомпланарных векторов равно по модулю параллелепипеду, построенного на этих векторах.

48. Предложение 4 об объеме параллелепипеда.

49. Предложение 5 о равенстве 0 для СмП.

СмП=0, только когда его сомножители компланарны:

1.

2. - компланарны, когда компланарны

3. _┴ лежит в плоскости

50. Свойство линейности СП.

51. Предложение 6 о линейности ВП.

, где – произвольный вектор.

52. Выражение векторного и смешанного произведения через компоненты сомножителей.

Если вместо вектора подставить базисно-единичные вектора , , , то получим равенство соответствующих компонентов векторов в формуле (пункт 51).

53. Теорема 2 о представлении векторного произведения.

В ортоганальном базисе векторное произведение выражается через компоненты следующим образом:

54. Теорема 3 о представлении смешанного произведения.

Смешанное произведение выражается через компоненты по формуле:

, , .

, где - смешанное произведение базисных векторов.

55. Детерминанты, 2-го и третьего порядка в связи с ВП и СмП.

– векторное произведение через детерминант 3-го порядка.

56. Представление выражения для ВП через Детерминант 2-го порядка.

- детерминант 2-го порядка.

– ВП через детерминант 2-го порядка.

57. Представление выражения для СмП через Детерминант 3-го порядка.

- СмП через детерминант 3-го порядка.

58. Выражение решения системы 3-го порядка через СмП.

59. Связь свойства линейности СмП и Свойствами Детерминанта.

60. Условия коллинеарности и компланарности векторов.

Два вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой.

Три вектора называются компланарными, если они лежат на параллельных плоскостях или в одной плоскости.

61. Предложение 7. О попарных ВП.

Попарное векторные произведения базисных векторов линейно независимо.

62. Предложение 8 Н и Д условие компланарности 3-х векторов.

Для компланарности 3-ёх векторов необходимо и достаточно обращение в «0» детерминанта матрицы.

Если тройка содержит пару коллинеарных векторов, то она компланарна.

63. Предложение 9. Н и Д условие коллинеарности 2-х векторов (в пр-ве).

Если векторное произведение двух векторов равно 0, то эти векторы коллинеарны.

64. Предложение 10. Н и Д условие коллинеарности 2-х векторов (на пл-ти).

Если векторное произведение двух векторов равно 0, то эти векторы коллинеарны.

65. Площадь параллелограмма на 2-х векторах (в пространствеве) и (на плоскостити).

– на плоскости и пространстве.

66. Понятие ориентированного параллелограмма.

67. Объем ориентированного параллелепипеда Предложение 11.

68. Понятие ориентированного параллелепипеда.

Ориентированный параллелограмм – это смешанное произведение 3-ёх векторов, на которых построен параллелограмм.

69. Двойное векторное произведение Доказательство формулы.

– Формула Лагранжа.

Доказателство – см. приложение 1.

70. Взаимный базис Определение.

Взаимный базис – это вспомогательная система координат.

71. Предложение 12 . О компонентах векторов во взаимном базисе.

72. Предложение 13 .О базисе, взаимном для взаимного базиса.

73. О векторных величинах.

74. Изменение базиса.

Рассмотрим изменение 2-ух систем координат, где М-произвольная точка, координаты которй в системе равны. Нам известны координаты нового и старого . По правилу сложения векторов имеем:

.

75. Формулы , связывающие компоненты векторов в разных базисах (в пространстве) и (на плоскости).

В пространстве:

На плоскости:

76. Изменение системы координат (в пространстве) и (на плоскости).

77. Преобразование декартовой прямоугольной системы координат на плоскости.

78. Определение уравнения линии, поверхности, множества.

Линия – траектория движения точки в каждый момент времени.

_{равно нулю.}

Алгебраической поверхностью называется множество , которое в некоторой ДСК может быть описано следующим уравнением: , где , целые числа, max( , ) называется степенью уравнения и является порядком поверхности. Аналогично определение алгебраической линии.

Параметрическое уравнение движения поверхности.

.

79. Предложение 1 об уравнении пересечения 2-х множеств.

Пусть Р₁ и Р₂ – уравнение множеств S и T, то уравнение их пересечения - есть высказывание Р₁ и Р₂ верно единовременно.

80. Предложение 2 об уравнении объединения 2-х множеств.

Пусть Р₁ и Р₂ – уравнение множеств S и T, то уравнение их объединения (суммы) (SvT), состоит в том, что верно либо Р₁ либо Р₂.

81. Предложение 3 об уравнении подмножества.

Пусть Р₁ и Р₂ – уравнение множеств S и T, если S подмножество (часть) множества T, то из Р₂→Р₁ и наоборот из Р₁→Р₂.

82. Предложение 4 о совпадении 2-х множеств.

83. Алгебраические линия и поверхности.

Алгебраической поверхностью называется множество , которое в некоторой ДСК может быть описано следующим уравнением: , где , целые числа, max( , )называется степенью уравнения и является порядком поверхности. Аналогично определение алгебраической линии.

84. Определение уравнения алгебраической линии.

85. Определение уравнения алгебраической поверхности.

86. Теорема 1 об инвариантности порядка линии.

87. Теорема 2 об инвариантности порядка поверхности.

88. Параметрические уравнения линии (на пл-ти) и (в пр-ве).

Представим себе, что линия- это есть траектория движущейся точки (самолет, катер и т.д.) и в каждый момент времени известно положение точки:

Величина t называется параметром. Поэтому эти уравнения называются параметрическими уравнениями линий в пространстве.

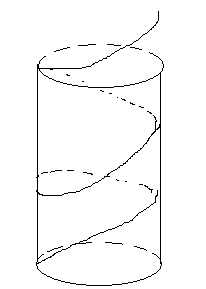
Z=at

89. Параметрические уравнения поверхностей.

Аналогично, но зависит от двух параметров – параметрическое уравнение поверхности в пространстве:

Х=

90. Параметрические уравнения конуса.

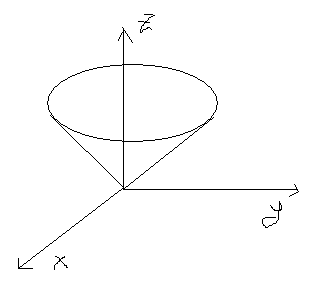
91. Уравнения, не содержащие одной из координат.

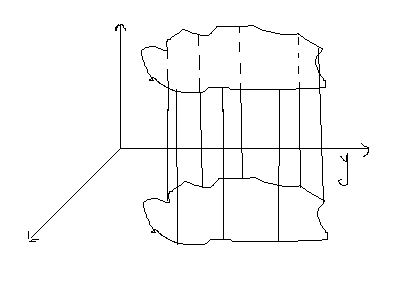Рассмотрим ДСК в пространствеРассмотрим некоторое уравнение в плоскости (х,у) у образующие, цилиндрическая поверхность

Если мы рассмотрим это уравнение в пространстве , то увидим. Что нет координаты z ,то есть оно справедливо для любого z.

92. Определение уравнения цилиндрической поверхности, Образующая. Направляющая.

Поверхность, которая состоит из прямых линий, параллельных заданному направлению (здесь ось z) называется цилиндрической поверхностью или цилиндром, а прямые линии – образующими.

П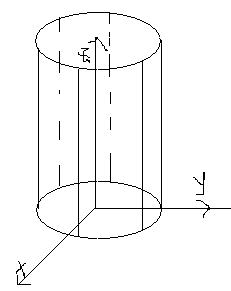 ример:

93. Поверхности и линии первого порядка.

Уравнения первой степени, связывающие координаты точки в пространстве, имеют вид: Ах+Ву+Сz+D=0 (1) уравнение плоскости,

На плоскости: Ах+Ву+Сz=0 (2) ,уравнение прямой

94-95. Теорема 1,2 об уравнении плоскости и прямой.

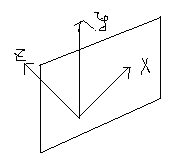В общей ДСК в пространстве каждая плоскость может быть задана линейным уравнением(на плоскости – каждая прямая). И наоборот: каждаое линейное уравнение (1) в ДСК определяет плоскость (уравнение(2)- прямую на плоскости)

Док-во:

z=0

Сделаем замену переменной:=

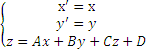
В новой системе координат уравнение будет , что и доказано в теореме.

Обратно:

Х=х’

Y=y’

Z=-