4.2.Вычисление криволинейного интеграла по координатам
Вычисление криволинейного интеграла по координатам сводится к вычислению определенного интеграла. В зависимости от способа задания кривой интегрирования АВ различают следующие случаи:
1.
Кривая АВ
задана уравнением
,
.
Подставляя
и
в (3.2), получим
(3.3)
2.
Кривая АВ
задана уравнением
,
.
Подставляя
,
в (3.2), получим
(3.4)
3.
Кривая АВ
задана параметрическими уравнениями
и значению
соответствует точка А,
а значению
– точка В.
Подставим х,
у,
,
в (3.2), получим
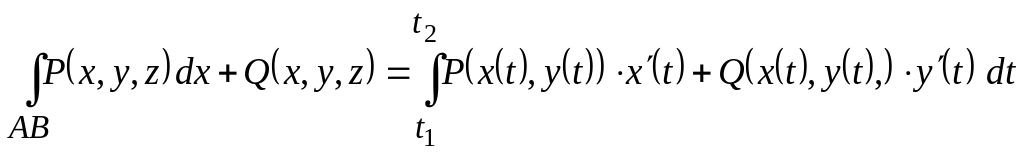(3.5)
Аналогично
определяется криволинейный интеграл
второго рода от непрерывных функций
,
,
в точках пространственной кривой AB,
когда кривая АВ
задана параметрическими уравнениями
,
,
:
Замечание.
Если линия интегрирования АВ
– отрезок прямой, соединяющий точки
и
,
то уравнение удобно записать как
уравнение прямой, проходящей через эти
точки:
(3.6)
Пример 1. Вычислить криволинейный интеграл
вдоль
линии L,
где L
– отрезок прямой от точки
до точки
.
Решение.
Используя формулу (3.6), запишем уравнение
линии интегрирования ОА:
или
.
При движении из точки О
в точку А х
меняется от 0 до 1, поэтому по формуле
(3.3.) имеем:
.
Пример 2. Вычислить криволинейный интеграл
вдоль
линии L
– ломаной
ОАВ:
где
,
,
.
Р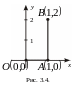
ешение.
Изобразим линию интегрирования ОАВ
(рис.3.4), данный интеграл равен сумме
двух интегралов:
.
Отрезок ОА
задается таким уравнением
,
где переменная интегрирования х
изменяется от 0 до 1. Подставляя
и
в формулу (3.3) получим:
Отрезок АВ
задается уравнением
где переменная интегрирования y
изменяется от 0 до 2. Подставляя
и
в формулу (3.4) получим:
Таким образом имеем:
Пример 3.
Вычислить криволинейный интеграл
,
если L
– дуга эллипса
,
,
лежащая в 1-ом координатном углу и
пробегаемая против хода часовой стрелки
(рис.3.5.).
Р
ешение.
Линия интегрирования L
задана в параметрическом виде (случай
3).Вычислим dx и dy:
,
.
Подставляя значения x, y, dx и dy, согласно формуле (3.4) получим определенный интеграл по переменой t.
Пример 4. Вычислить криволинейный интеграл
вдоль периметра
,
где
;
,
,
совершая обход против часовой стрелки
(рис.3.6.).
Решение. Т.к. линия интегрирования состоит из трех отрезков, то соответственно этому криволинейный интеграл по ломаной АСВA вычислим как сумму интегралов, взятых по отрезкам АС, СВ и ВА.
1. Уравнение
АС:
.
Переменная интегрирования х
изменяется от -1 до 2. Найдем
.
Подставляя
и
в данный криволинейный интеграл, согласно
формуле (3.3) получим
.
2. Уравнение
прямой СВ составим по формуле (3.6):
или
.
На отрезке СВ:
переменная интегрирования у
изменяется от 0 до 2. Находим
.
Подставляя х и
в данный криволинейный интеграл, согласно
формуле (3.4) получим
.
3. Уравнение
прямой АВ составим по формуле (3.6):
или
.
Переменная интегрирования х на
отрезке АВ изменяется от 0 до -1.
Находим dy:
.
Подставляя у и dy в данный криволинейный интеграл, согласно формуле (3.3) получим:
Итак:
.