2.Двойной интеграл

2.1.Определение и свойства двойного интеграла

Пусть в некоторой ограниченной замкнутой области D плоскости xОy задана непрерывная функция .

Р азобьем эту область произвольным образом на n частичных плоских ячеек с площадями , , …, .

Диаметром i-ой ячейки называется наибольшее из расстояний между ее точками. В каждой ячейке выберем по одной произвольной точке , , ..., и вычислим значения функции f(P) во взятых точках. Составим так называемую интегральную сумму функции в области D:

. (1.1)

Двойным интегралом от функции по области D называется предел интегральных сумм (1.1) при стремлении к нулю наибольшего из диаметров всех ячеек данного разбиения:

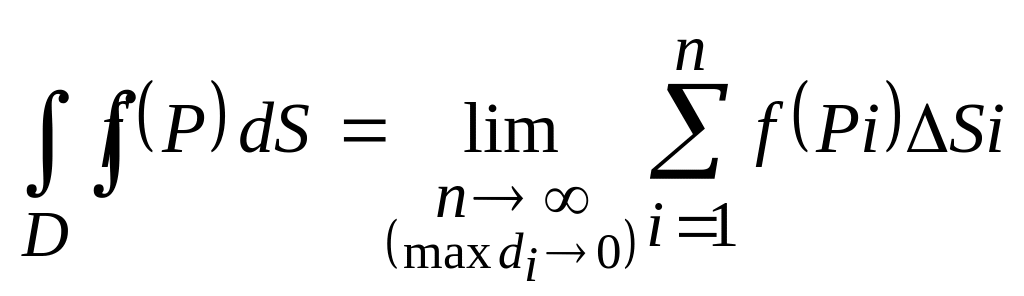. (1.2)

Если подынтегральная функция , то значение двойного интеграла равно площади области интегрирования D:

. (1.3)

Основные свойства двойного интеграла

1. Двойной интеграл от алгебраической суммы функций равен алгебраической сумме двойных интегралов слагаемых функций:

_.

2. Постоянный множитель можно выносить за знак двойного интеграла: если , то

3. Область интегрирования двойного интеграла можно разбивать на части, т.е. если область D состоит из двух областей и , то

_.

2.2.Рекомендации по выбору системы координат и алгоритм вычисления двойного интеграла

Во многих случаях вычисление двойных интегралов значительно упрощается, если перейти от декартовой системы координат к полярной, учитывая вид области интегрирования или подынтегральной функции. (Подробно, полярная система координат и построение кривых в ней рассмотрены в Приложении). Выбирают полярную систему координат при расчетах двойных интегралов на практике, как правило, в следующих случаях:

По виду области:

1. Если уравнения линий, ограничивающих область, сразу записаны в полярной системе координат:

а) D: (окружность, рис. 1.2.);

б) D: (лемниската, рис. 1.3.).

Следует отметить, что кривые, соответствующие таким уравнениям ограничены и обладают свойством симметрии либо относительно оси , либо относительно оси , либо относительно обеих осей одновременно (рис.1.3.).

2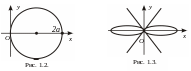 . Если область интегрирования D представляет собой круг, круговой сектор, кольцо или его часть.

3. Если в декартовой системе координат хотя бы одно из уравнений линий, ограничивающих область D (как в выше перечисленных областях), содержит двучлен .

а) D: (окружность, рис. 1.2.);

б) D: (лемниската, рис. 1.3.).

По виду подынтегральной функции:

1. Если интеграл сразу записан в полярной системе координат. Например: или .

2. Если подынтегральная функция является функцией от . Например: .

Таким образом, вычисление двойного интеграла удобно производить по следующему алгоритму:

1. Построить область интегрирования D по данным задачи.

2. Учитывая вид области интегрирования и подынтегральной функции, выбрать систему координат, в которой рационально производить вычисления.

3. Выполнить замену переменных в интеграле, если это необходимо.

4. Определить, является ли область интегрирования простой, и относительно какой оси. Если нет, то представить ее как сумму простых. Для экономии вычислительной работы следует, если это возможно, выбирать такое направление, при котором не нужно область интегрирования разбивать на части – простые области.

5. Для каждой простой области записать двукратный интеграл и расставить пределы интегрирования (не забудьте, что у внешнего интеграла, они всегда постоянные).

6. Вычислить двукратный интеграл по правилам.

Помните, что вначале вычисляется внутренний интеграл по заданной переменной при постоянных значениях остальных переменных, а затем – внешний.