3.3.Вычисление объемов тел с помощью тройных интегралов
Объем тела , как было отмечено в пункте 2.1., формула (2.3), равен:
,
тогда в декартовых и цилиндрических координатах, объем вычисляется по формулам:
(2.9)
(2.10)
П
ример
14. Вычислить объем
тетраэдра, ограниченного плоскостями:
,
,
и
.
Решение. Построим область интегрирования, в данном случае это тетраэдр (рис. 2.20.). Проекция тетраэдра на плоскость служит треугольник, образованный прямыми
,
и
,
так что
изменяется от 0 до 6, а при фиксированном
изменяется от 0 до
(рис. 2.21.). Если же фиксированы и
,
и
,
то точка может перемещаться по вертикали
от плоскости
до плоскости
,
т.е.
меняется в пределах от 0 до
.
По формуле (2.6) при
получаем
П
ример15.
Вычислить объем тела, ограниченного
цилиндрической поверхностью
и плоскостями
,
,
.
Решение. Для
вычисления объема тела воспользуемся
формулой (2.6). Из рис. 2.22. видно, что
интегрирование рационально при
проецировании области
в область
плоскости
,
при этом
и
.
Для получения
границы области
исключим из уравнений параболического
цилиндра
и плоскости
переменную
и получим уравнение
,
которое определяет в плоскости
параболу (рис. 2.23.). Таким
образом, граница области
состоит из дуг ветвей параболы (
и
)
и отрезков прямых
,
.
Следовательно,
Пример 16.
Найти объем тела, ограниченного
поверхностями:
и
,
,
.
Решение.
Изобразим тело и его проекции на плоскость
(рис. 2.24. и рис. 2.25.). Снизу и сверху тело
ограничено плоскостями
и
соответственно. С боку – параболическим
цилиндром
и прямым круговым:
,
с образующими параллельными оси
.
О
бласть
интегрирования является простой
относительно оси
(случай как на рис. 2.2.).
Но так как тело
симметрично, то подсчитаем по формуле
(2.6) только объем половины, проектирующейся
в область
:
.
Область будем считать простой относительно оси , по формуле (1.5) получим:
.
Пример 17.
Вычислить объем тела, ограниченного
поверхностями
,
и плоскостью
.
Решение. Область , (рис. 2.26.) ограничена снизу , сверху - параболоидом , сбоку – цилиндрической поверхностью , образующие которой параллельны оси . Поэтому область проецируется на плоскость в область , ограниченную окружностью (рис. 2.27.).
Следовательно,
для вычисления интеграла целесообразно
перейти к цилиндрическим координатам.
Применяя формулу (2.10), и учитывая, что
уравнение параболоида в цилиндрической
системе координат имеет вид
и симметрию тела относительно обеих
координатных плоск
остей
и
получим:
.
4.Криволинейный интеграл по координатам (второго рода)
4.1.Определение и свойства криволинейного интеграла
П
усть
дана дуга кривой на плоскости
,
имеющая начало в точке А
и конец в точке В
(см. рис. 3.1), на которой задана пара
непрерывных функций
и
.
Дугу АВ
разобьем произвольными точками на n
элементарных дуг
,
проекции которых на оси Ох
и Оу
обозначим через
и
.
На каждой i-ой
дуге
выберем точку
,
вычислим значения функций в этой точке
и
и составим интегральную сумму (3.1).
(3.1)
Криволинейным
интегралом
по координатам (второго рода), взятым
по кривой АВ,
называется предел n-ой
интегральной суммы (3.1) при
и стремлении к нулю длины наибольшей
из элементарных дуг (
при
),
то есть
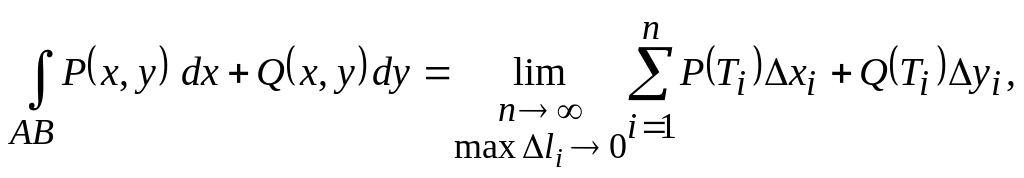(3.2)
Некоторые свойства криволинейного интеграла по координатам:
1.
Значение криволинейного интеграла
зависит от выбора направления обхода
кривой. Если изменить направление
обхода, то интеграл меняет знак:
.
2.
Кривую интегрирования можно разбить
на части точкой С,
тогда
.
3. Криволинейный интеграл по замкнутой кривой не зависит от выбора начальной точки на этом контуре (зависит только от направления обхода кривой).
З
амечание.
Криволинейный интеграл по координатам
зависит от направления интегрирования.
В случае, когда контур интегрирования
замкнут, из двух возможных направлений
обхода положительным условились называть
обход его против часовой стрелки (рис.
3.2.), а интеграл 3.2. записывается в виде:
.