
- •Кратные и криволинейные интегралы
- •Оглавление
- •Библиографический список………………………………………………50
- •1.Введение
- •2.Двойной интеграл
- •2.1.Определение и свойства двойного интеграла
- •2.2.Рекомендации по выбору системы координат и алгоритм вычисления двойного интеграла
- •2.3.Вычисление двойного интеграла в декартовой системе координат
- •2.4.Вычисление двойного интеграла в полярной системе координат
- •3.Тройной интеграл
- •3.1.Определение и свойства тройного интеграла
- •3.2.Вычисление тройного интеграла в декартовых координатах
- •3.3.Вычисление объемов тел с помощью тройных интегралов
- •4.Криволинейный интеграл по координатам (второго рода)
- •4.1.Определение и свойства криволинейного интеграла
- •4.2.Вычисление криволинейного интеграла по координатам
- •Приложения
- •Понятие о полярной системе координат
- •Кривые второго порядка
- •Поверхности второго порядка
2.4.Вычисление двойного интеграла в полярной системе координат
Прежде, чем приступить к изучению данной темы, обратитесь к Приложению. Повторите понятие о полярной системе координат и построение линий в ней.
Формула преобразования двойного интеграла от декартовых координат х и у к полярным и , связанным с декартовыми соотношениями
![]() и
и
![]() (1.9)
(1.9)
имеет вид:
![]() , (1.10)
, (1.10)
где и - полярные координаты точек области D.
При этом уравнения линий, ограничивающих область интегрирования D, также записываются в полярной системе координат посредством формул (1.9).
Отметим, что
![]() , (1.11)
, (1.11)
т.к.
![]() .
.
Текущая точка Р
области D имеет
координаты
![]() ,
а площадь элементарной ячейки
,
а площадь элементарной ячейки
![]() .
.
Вычисление двойного интеграла в полярных координатах сводится к вычислению декартовых (повторных) интегралов по и по по формулам (1.12 – 1.14), в которых в вначале вычисляется внутренний интеграл по переменной при фиксированном, но произвольном .
Различают следующие виды области D.
Область D (рис. 1.21.) ограничена лучами образующими с полярной осью углы
 и
и
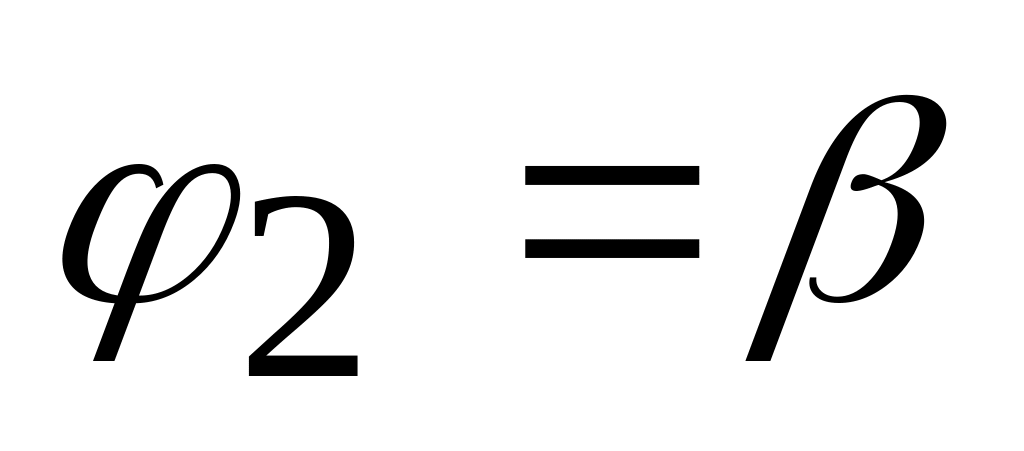 ,
и кривыми
,
и кривыми
 и
и

 то:
то:
 .
(1.12)
.
(1.12)
Ф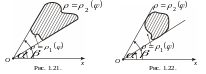 ормула
(1.12) справедлива, если отрезки лучей
ормула
(1.12) справедлива, если отрезки лучей
![]() и
и
![]() стягиваются в точки (рис. 1.22.).
стягиваются в точки (рис. 1.22.).
О
 бласть
D охватывает начало
координат рис. 1.23., то
бласть
D охватывает начало
координат рис. 1.23., то
![]() .
(1.13)
.
(1.13)
Область интегрирования D не удовлетворяет условиям, сформулированным в пп. 1 и 2. В этом случае нужно разбить на части, обладающими отличительными свойствами.
Площадь плоской фигуры в полярной системе координат вычисляется по формуле:
![]() (1.14)
(1.14)
П ример
10. Вычислить
ример
10. Вычислить
![]() ,
где область D - круговой
сектор, ограниченный линиями:
,
где область D - круговой
сектор, ограниченный линиями:
![]() ,
,
![]() ,
,
![]() .
.
Решение.
Построим область интегрирования (рис.
1.24.). Это область D
второго вида:
![]() ,
,
![]() ,
,
![]() .
.
Согласно (1.13):
![]()
![]()
![]()
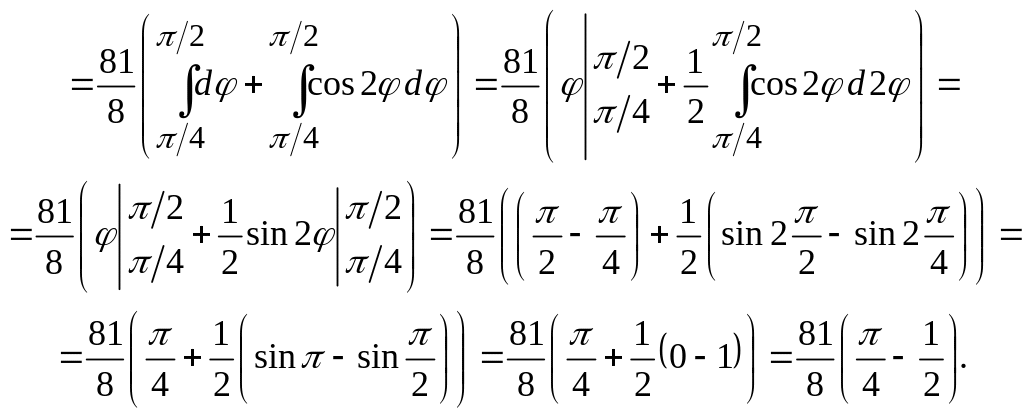
Вычисление двойного
интеграла началось с внутреннего
определенного интеграла по ,
это
![]() ,
а затем был вычислен внешний интеграл
по
,
а затем был вычислен внешний интеграл
по
![]() .
При вычислении внутреннего интеграла
множитель
.
При вычислении внутреннего интеграла
множитель
![]() вынесен за знак внешнего интеграла.
вынесен за знак внешнего интеграла.
Пример 11. Вычислить в полярных координатах
![]()
г де
D – область, ограниченная
линиями:
де
D – область, ограниченная
линиями:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Решение. Область интегрирования D – часть кругового кольца, отсеченная двумя лучами, исходящими из полюса (см. рис.1.25.).
1. Запишем уравнение линий, ограничивающих область, в полярной системе координат с помощью формул (1.11).
Уравнение СВ:
![]() или
или
![]() .
.
Уравнение АD:
![]() или
или
![]() .
.
Прямая СD:
– биссектриса, поэтому
![]() .
.
Прямая АВ:
,
![]() ,
,
![]() .
.
Итак, область D
принадлежит к 1-му виду:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
2. Запишем заданный двойной интеграл в полярной системе координат по формуле (1.12), делая сразу замену переменных в подынтегральной функции по формуле (1.11).
Получаем
![]()
![]()
![]()
Отметим, что вначале
вычислен внутренний интеграл, определенный
по - это
![]() Результат вычисления – число 136 вынесено
за внешний интеграл, после чего вычислен
внешний определенный интеграл по
переменной .
Результат вычисления – число 136 вынесено
за внешний интеграл, после чего вычислен
внешний определенный интеграл по
переменной .
Пример 12.
Вычислить площадь фигуры, ограниченной
прямыми
![]() ,
и окружностью
,
и окружностью
![]() .
.
Решение. Введем полярные координаты. Сделаем эскиз области интегрирования (рис. 1.26.). Перепишем уравнение линий в полярной системе координат с помощью формул (1.9 и 1.11).
У равнение
окружности
в виде
равнение
окружности
в виде
![]() (см. пример 11).
(см. пример 11).
Прямых:
как
![]() ,
,
![]() как
.
как
.
Получили область
D второго вида как на
рис.1.23:
![]() ,
,
![]() ,
,
![]() .
.
Площадь фигуры вычислим по формуле (1.14), а двойной интеграл по (1.13):
![]()
![]()
![]()
![]()
![]()
При вычислении внешнего интеграла применена формула:
![]() .
.
Пример 13. Вычислить площадь фигуры, ограниченной кривой
![]() .
.
Р ешение.
Сделаем эскиз области интегрирования
(рис.1.27.). Левая часть уравнения
ешение.
Сделаем эскиз области интегрирования
(рис.1.27.). Левая часть уравнения
![]() ,
тогда
,
тогда
![]() ,
т.е. х и у имеют одинаковые знаки.
Следовательно, кривая расположена в 1
и 3 координатных углах. При замене х
и у на
,
т.е. х и у имеют одинаковые знаки.
Следовательно, кривая расположена в 1
и 3 координатных углах. При замене х
и у на
![]() и
и
![]() уравнение не меняется, значит, кривая
симметрична относительно начала
координат. С помощью формул (1.9) и (1.11)
перепишем уравнение линии в полярной
системе координат:
уравнение не меняется, значит, кривая
симметрична относительно начала
координат. С помощью формул (1.9) и (1.11)
перепишем уравнение линии в полярной
системе координат:
![]()
![]() ,
,
сократим на
![]() ,
получим окончательно
,
получим окончательно
![]()
С возрастанием
от 0 до
![]() точка с координатами
опишет расположенную в 1 координатном
углу ветвь данной кривой.
точка с координатами
опишет расположенную в 1 координатном
углу ветвь данной кривой.
Искомая площадь равна удвоенной площади области D, которая является областью 2-го вида (рис.1.27).

![]()
![]()
