3.Тройной интеграл

3.1.Определение и свойства тройного интеграла

П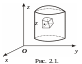 усть в ограниченной замкнутой пространственной области задана непрерывная функция . Разобьем эту область произвольным образом на частичных пространственных ячеек с объемами , , …, (рис. 2.1.). В каждой ячейке выберем по одной произвольной точки , , …, и вычислим значение функции во взятых точках по области . Составим интегральную сумму вида:

. (2.1)

Тройным интегралом от функции по области называется предел интегральных сумм (2.1) при стремлении к нулю наибольшего из диаметров всех ячеек данного разбиения:

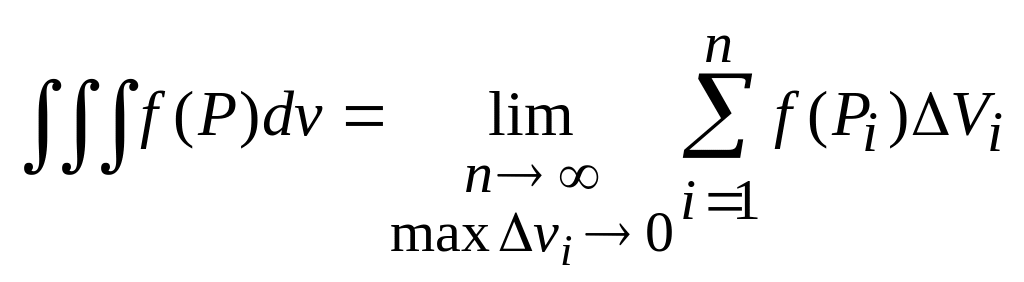. (2.2)

Если подынтегральная функция , то значение тройного интеграла равно области интегрирования:

. (2.3)

Основные свойства тройного интеграла:

Свойства тройных интегралов аналогичны свойствам двойных интегралов. Перечислим основные их них:

1. Тройной интеграл от алгебраической суммы функций равен сумме тройных интегралов от слагаемых функций:

.

2. Постоянный множитель можно вынести за знак тройного интеграла:

.

3. Область интегрирования тройного интеграла можно разбить на части, т.е. если область состоит из двух областей и , то:

.

3.2.Вычисление тройного интеграла в декартовых координатах

Тройной интеграл в декартовых координатах записывается в виде:

. (2.4)

Текущая точка области интегрирования имеет координаты , а элементарную ячейку можно считать параллелепипедом со сторонами , , , то есть ее объем .

Вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов, т.е. к трехкратному интегралу. Эти кратные интегралы записывают для простых, относительно осей координат, областей интегрирования . Если же область не является простой, то ее представляют в виде суммы простых.

Р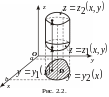 ассмотрим, например, область интегрирования относительно оси (для других осей определения аналогичны).

Область называется простой относительно оси , если она проецируется в область на плоскости так, что любая прямая, параллельная оси и проходящая внутри области , пересекает границу области только в двух точках (рис. 2.2). Это означает, что область ограничена снизу поверхностью , сверху – поверхностью и с боков – цилиндрической поверхностью с образующими, параллельными оси , которая может стягиваться в линию.

Для такой области V тройной интеграл вычисляется по формуле

. (2.5)

В формуле (2.5) вначале берется внутренний интеграл по при фиксированных, но произвольных в области значениях и у. В результате получается двойной интеграл по плоской области от некоторой функции . Если область ограничена линиями , , , , то, переходя от двойного интеграла к повторному получаем формулу

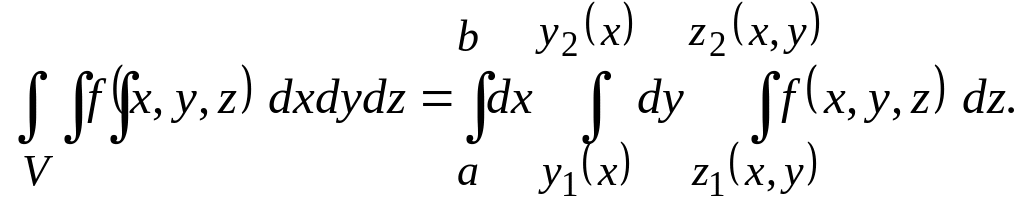(2.6)

Наиболее простой вид формула (2.6) принимает в случае, когда в область интегрирования – прямоугольный параллелепипед, ограниченный плоскостями , , , , , :

(2.7)

Чтобы вычислить тройной интеграл, необходимо построить область интегрирования V и ее проекцию D.

Е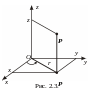 сли проекция представляет собой часть круга, кругового сектора, кольца, то вычислять тройной интеграл проще в цилиндрических координатах (рис. 2.3.).

Цилиндрические координаты , , z связаны с прямоугольными координатами следующими соотношениями:

где , , .

Тройной интеграл в цилиндрических координатах имеет вид:

(2.8)

где - элемент объема в цилиндрических координатах.

Так как при выполнении задания необходимо изобразить тело и его проекцию на плоскость , то ниже приведем уравнения, чертежи линий и поверхностей наиболее часто встречающиеся при решении задач.

1. – уравнение прямой в плоскости .

Е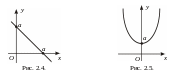 сли , то – точка пересечения прямой с осью ; если , то – точка пересечения прямой с осью , при (рис. 2.4.).

2. – уравнение параболы, ось симметрии ось , вершина в точке , при (рис. 2.5.).

3 . – уравнение окружности с центром в точке и радиусом на плоскости (рис. 2.6.).

Уравнения половин окружностей, изображённых на рис. 2.7. и рис. 2.8. соответственно будут и .

4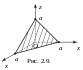 . – уравнение плоскости, пересекающей все координатные плоскости:

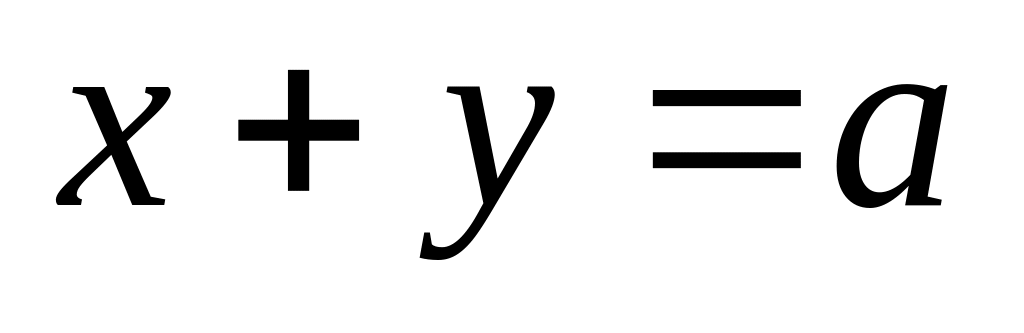
• по прямой 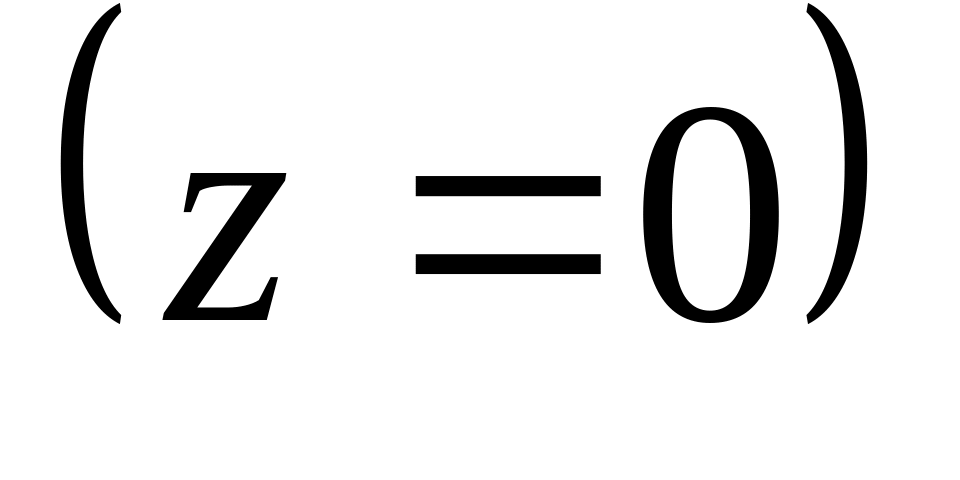– плоскость ;

• по прямой – плоскость ;

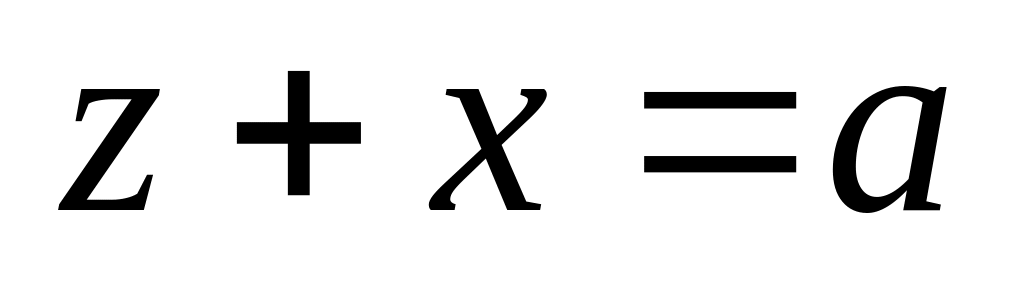
• по прямой – плоскость (рис. 2.9).

5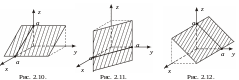 . – уравнение плоскости, параллельной оси и отсекающей на осях и в точках и (рис. 2.11).

6. – уравнение плоскости, параллельной оси и отсекающей на осях и отрезки и (рис. 2.10.).

7. – уравнение плоскости, параллельной оси и отсекающей на осях и отрезки и (рис. 2.12).

8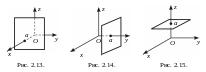 . , и – уравнение плоскостей, параллельных соответственно координатным плоскостям , и пересекающих оси , и в точках (рис. 2.13.), (рис. 2.14.), и (рис. 2.15.).

9. – уравнение прямого кругового цилиндра, образующие которого параллельны оси (рис. 2.16.)

1 0. – уравнение параболоида вращения с вершиной в , осью симметрии – (рис. 2.17.).

1 1. , – уравнение параболических цилиндров, образующие которых параллельны оси и оси соответственно, а направляющие – параболы на плоскости и соответственно (рис. 2.18., .2.19.).