2.3.Вычисление двойного интеграла в декартовой системе координат

Двойной интеграл (1.2) в декартовой системе координат хOу записывается в виде:

. (1.4)

Текущая точка P области интегрирования D имеет координаты , тогда элементарную ячейку можно считать прямоугольной со сторонами dx и dy, то есть ее площадь .

Вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов – к двукратному (повторному) интегрированию по формулам (1.5-1.8). Порядок интегрирования по переменным x и y в двукратных интегралах (выбор формулы) зависит от области интегрирования D. На практике, как правило, выбирают такой порядок интегрирования, при котором не нужно разбивать область на части.

Р азличают следующие виды областей интегрирования:

1. Область D на плоскости хОу является простой относительно оси Ох, т.е. проецируется в некоторый отрезок оси Ох так, что любая прямая, параллельная оси Oy и проходящая внутри отрезка , пересекает границу области (линии и на рис.1.4. и 1.5.) в двух точках.

В этом случае вычисление двойного интеграла сводится к вычислению двукратного интеграла по следующей формуле:

. (1.5)

Вычисления начинаются с внутреннего интеграла , который берется по у при фиксированном, но произвольном на отрезке , значении х. В результате получается некоторая функция от х, которая затем интегрируется в пределах от a до b.

З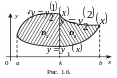 амечание. Если нижняя или верхняя граница области D состоит из нескольких участков, имеющих различные уравнения, то область D следует разбить на части прямыми, параллельными оси Оy и проходящими через точки, в которых «стыкуются» различные участки границы. Например, для области D, изображенной на рис.1.6., вычисление двойного интеграла осуществляется по формуле

. (1.6)

2 . Область D на плоскости xOy – простая относительно оси Оy, т.е. проектируется в некоторый отрезок оси Oy так, что любая прямая, параллельная оси Ox и проходящая внутри отрезка , пересекает границу области (линии и на рис. 1.7. и 1.8. в двух точках).

В этом случае вычисление двойного интеграла сводится к вычислению двукратного интеграла по следующей формуле:

(1.7)

Вычисление начинается с внутреннего интеграла по переменной х при фиксированном значении у.

З амечание. Если левая или правая граница области D состоит из нескольких участков, имеющих различные уравнения, то область D следует разбить на части прямыми, параллельными оси Ох и проходящими через точки, в которых «стыкуются» различные участки границы.

Например, для области D, изображенной на рис. 1.9., вычисление двойного интеграла осуществляется по формуле:

(1.8)

3. Если область D одновременно является простой, относительно осей Ox и Oy, то при вычислении двойного интеграла применимы обе формулы (1.5) и (1.7), т.е.

При этом надо выбирать ту из двух указанных формул (такой порядок интегрирования), которая приводит к наиболее простым вычислениям.

4. Если область D не удовлетворяет условиям, сформулированным в п.1 и 2, то в этом случае ее надо разбить на конечное число областей , , ..., , каждая из которых удовлетворяет этим условиям. Тогда

Пример 1. Вычислить двойной интеграл

,

где D ограничена параболой и прямыми и . Вычисления провести двумя способами (рассмотреть область D относительно оси Ох и оси Оу) и сравнить результаты.

Р ешение. Изобразим область интегрирования D (рис. 1.10.). Найдем координаты точки пересечения графиков функций и . Для этого совместно решим эти два уравнения. Получим , .

1 способ. Рассмотрим область D относительно оси Ох. Ее вид соответствует рис.1.6., то есть прямой ее необходимо разбить на две области и ; при этом получится ; ; ; ; ; . Записываем соответствующий (рис. 1.6.) двукратный интеграл по формуле (1.6) и начинаем его вычисление с внутреннего интеграла по у при фиксированном значении х, а именно:

2 способ. Рассмотрим область D относительно оси Oy. Ее вид соответствует рис.1.7, то есть область является простой относительно оси Oy. Согласно рис.1.7., найдем: ; ; (разрешили уравнение относительно х); . Далее записываем по формуле (1.7) двукратный интеграл, в котором вначале вычисляем внутренний интеграл по х, считая у постоянной, а именно:

.

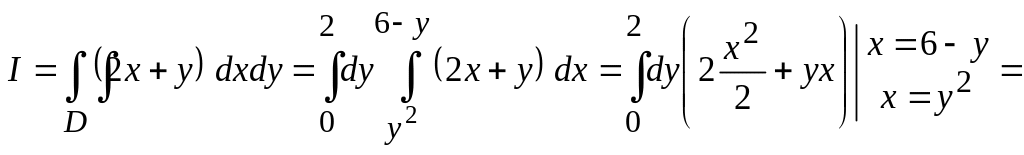
Проведем сравнение двух способов вычисления интегралов.

В рассмотренной задаче оказалось, что при любом порядке интегрирования двойной интеграл имеет одно и то же значение. Отметим, что это получилось не случайно. Значение двойного интеграла не зависит от порядка интегрирования. Однако, во втором случае, когда не было необходимости разбивать область интегрирования на части, вычисление интеграла было намного проще по сравнению с первым случаем. Поэтому для экономии вычислительной работы следует предварительно исследовать область интегрирования относительно осей и выбрать, если это возможно, такой порядок интегрирования, при котором не нужно разбивать область на части.

П ример 2. Вычислить , если D ограничена кривой и прямыми , , .

Решение. Построим область интегрирования D (рис.1.11.). В результате ее сравнения с областями на рис.1.3 – 1.9 установим, что она является простой только относительно оси Оу и такая же по виду как на рис.1.7., то есть ; ; ; . Двойной интеграл по такой области через повторный запишется по формуле (1.7) в виде:

В качестве упражнения на расстановку пределов интегрирования полезны задачи о перемене порядка интегрирования в повторном интеграле.

Пример 3. Изменить порядок интегрирования в интеграле

Р ешение. Из пределов интегрирования в повторном интеграле следует, что область интегрирования D соответствующего двойного интеграла ограничена прямыми и , снизу линией и сверху прямой . Область интегрирования D (рис. 1.12.) является простой относительно оси Ox, и имеет вид как на рис. 1.4. По пределам интегрирования заданного интеграла определяем в формуле (1.5): ; (уравнение прямой).

При

При

Поменяем порядок интегрирования переменных х и у в заданном интеграле, то есть будем рассматривать область D относительно оси Oy. Из рис.1.10. видно, что правая граница области состоит из трех различных участков, описывающихся различными уравнениями. В точках «стыковки» границ проведем прямые, параллельные оси Oх: , , которые разобьют область D на три простые области , и .

Тогда по свойству двойного интеграла получим:

.

Рассмотрим каждый из интегралов в отдельности в соответствии с рис.1.9.

Для области (разрешили уравнение относительно х: , перед корнем взяли знак «-», т.к. )

.

Для области

.

Для области (разрешили уравнение относительно x)

.

Окончательно имеем:

Пример 4. Изменить порядок интегрирования в двукратном интеграле

.

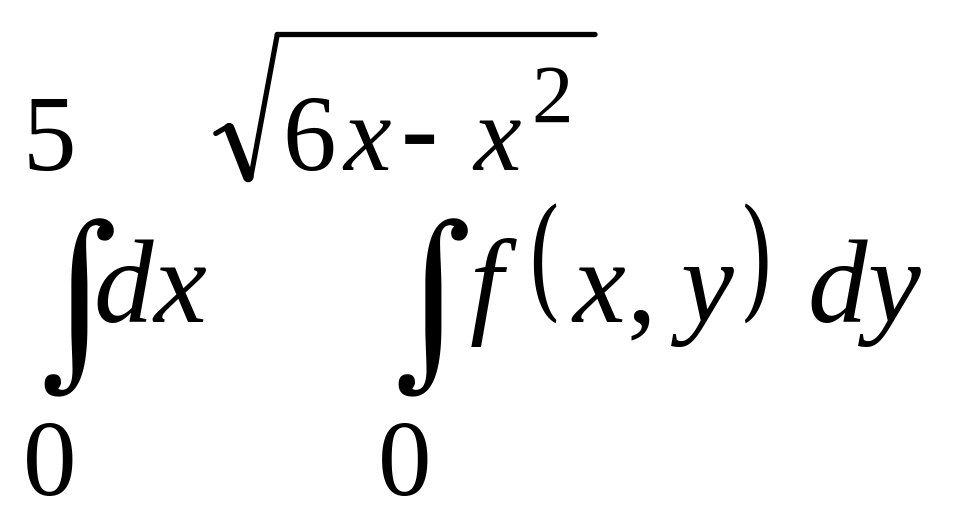Решение. Строим область интегрирования D (рис. 1.13.). Из структуры заданного двукратного интеграла следует (сравни с 1.5.), что область D является простой относительно оси Ox и имеет вид как на рис.1.4. или 1.5. По пределам интегрирования заданного интеграла определим: ; ; ; . При , ; при .

П окажем, что уравнение является уравнением окружности. Для этого возведем обе части уравнения в квадрат: и выполним следующие преобразования

;

(выделили полный квадрат по переменной х); – каноническое уравнение окружности с центром в точке и радиусом .

Поменяем порядок интегрирования по переменным х и у в заданном интеграле, т.е. рассмотрим область D относительно Оу. Правая граница области состоит из двух участков, описывающихся разными уравнениями: и (случай области как на рис.1.9.). Прямой разбиваем область D на две простые области и . Из рис.1.11. видно, что ; ; ; . Для нахождения функций и , описывающих дуги окружности, удобно разрешить каноническое уравнение окружности относительно х: ; . Тогда согласно (1.8) получим:

.

Пример 5. Изменить порядок интегрирования в повторном интеграле

.

Р ешение. Строим область интегрирования (рис.1.14.). По структуре заданного интеграла определяем (1.7), что область интегрирования D простая относительно оси Оу и должна выглядеть как на рис.1.7. или 1.8. из пределов интегрирования следует: , , (уравнение прямой).

Координаты точек «стыковки» границ находим из условий:

.

Поменяем порядок интегрирования переменных в заданном интеграле, то есть рассмотрим область D относительно оси Ox. Верхняя граница области D состоит из двух участков (как на рис.1.6.). В точке «стыковки» проведем прямую – область D разобьется на две простые и . Из рис.1.14. следует, что в формуле 1.6: ; ; (разрешили уравнение относительно у); (разрешили уравнение относительно у); . Ответ записывается в виде:

.
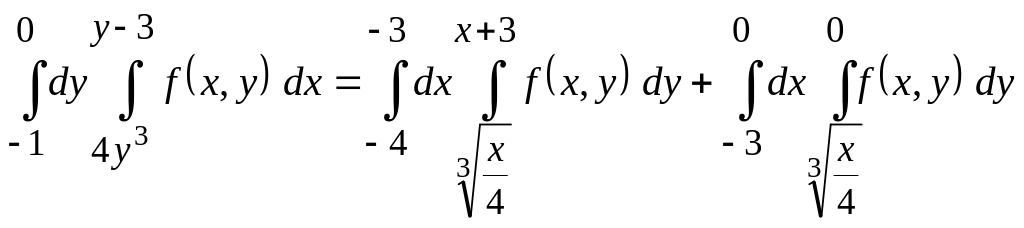