.42.3. Вычисление ширины интерференционных полос и расстояние между максимумами интенсивности.

Рис. 6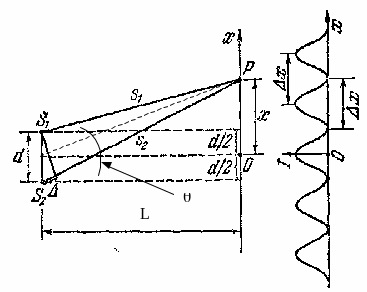

Сделаем рисунок. Здесь (рис.6) приняты обозначения: L – расстояние от источников до экрана,  - угол наблюдения, d – расстояние между источниками.

В точке O наблюдается так называемый нулевой максимум, т.к. в эту точку волны от обоих источников приходят в одинаковой фазе. Для того чтобы интерференционная картина была отчетливо различима, необходимо выполнение условия . Тогда из рисунка можно определить, что

.

Здесь x_m  расстояние от центра интерференционной картины до максимума с номером «m».

Следовательно,

.

Подстановка значения  дает, что максимум интенсивности будет наблюдаться при значениях:

.

Величина x_m также определяет расстояние от «0» максимума до максимума с номером «m».

Координаты минимума интенсивности определяются из условия:

, где m=0,1,2,…

Назовем расстояние между двумя соседними максимумами интенсивности расстоянием между интерференционными полосами, а расстояние между соседними минимумами интенсивности  шириной интерференционной полосы. Видно, что расстояние между полосами и ширина полосы имеют одинаковое значение, равное . Данное значение легко можно получить, если посчитать расстояние между двумя соседними максимума или минимумами. Рекомендуется расчет провести студентам самостоятельно. Из приведенного выражения следует, что для получения отчетливой интерференционной картины необходимо, чтобы выполнялось условие , о чем и говорилось выше.

Ширина интерференционных полос и расстояние между ними зависят от длины волны . Только в центре картины при x=0, совпадут максимумы всех длин волн. Если в установке Юнга источник испускает белый цвет, то только нулевой (главный) максимум окажется белым (здесь совпадут максимумы всех длин волн), все остальные максимумы будут окрашены. По мере удаления от центра максимумы разных длин волн (разных цветов) смещаются друг относительно друга все больше и больше. Это приводит к смазыванию интерференционной картины при наблюдении ее в белом цвете. В монохроматическом свете (монохроматическим называется свет, которому соответствует дона определенная длина волны) число различимых полос интерференции заметно возрастает.

Измерив расстояние между полосами x и зная значения L и d, можно вычислить . Именно из опытов по интерференции света были впервые определены длины волн для световых лучей разного цвета. Оранжево-красному участку спектра соответствуют более длинные волны (_к=780-600нм), а сине-фиолетовому – более короткие (_ф=480-420нм).

.52.4. Интерференция в тонких пленках.

Наиболее типичным и распространенным примером интерференции света в природе является интерференция в тонких пленках (мыльные пузыри, радужная пленка нефти на воде и т.д.).

Пусть на прозрачную тонкую пластинку толщиной d падает плоская световая волна под углом  (рис.7). Разность хода, приобретенная лучами 1 и 2 до того, как они сойдутся в точке С будет равна:

Рис. 7

,

где S₁=ВС; S₂=АО+ОС.

Но АО=ОС=d/cos, поэтому S₂=2d/cos.

В свою очередь ВС=АСsin, а АС=2АД=2dtg, поэтому S₁=2dtgsin.

Воспользовавшись приведенными равенствами и соотношением , получим, что

Для получения окончательной разности хода необходимо учесть, что световые волны, как и всякие другие волны, отражаясь от оптически более плотной среды (луч 1 в точке С) получают дополнительную разность фаз равную , т.е. возникает добавочная разность хода равная /2. При отражении от среды оптически менее плотной (точка О) скачка фазы не происходит.

Таким образом, при падении на пластинку плоской волны образуются две отраженные волны, разность хода которых определяется формулой:

В предположении, что лучи 1 и 2 когерентны, в результате падения на плоскопараллельную пленку пучка лучей в отраженном и проходящем свете на экране получаются чередующиеся темные и светлые полосы в случае монохроматического света и цветные полосы в случае белого света.

ДОПОЛНЕНИЕ 1.

Строго говоря, лучи 1 и 2 (или две плоские отраженные волны, распространяющиеся в одном направлении) смогут интерферировать, если будут соблюдены условия временной и пространственной когерентности.

Вспомним, что когерентностью называется согласованное протекание нескольких колебательных или волновых процессов. Степень согласованности может быть различной. Соответственно можно ввести понятие степени когерентности двух волн.

Различают временную и пространственную когерентность. Понятие когерентности является относительным: две волны могут вести себя как когерентные при наблюдении с одним прибором (с малой инерционностью) и как некогерентные при наблюдении с другим прибором (с большой инерционностью). Для характеристики когерентных свойств волн вводится время когерентности t_ког., которое определяет такое время, за которое случайное изменение фазы достигает значения ~. За время t_ког. колебание как бы забывает свою первоначальную фазу и становится некогерентным по отношению к самому себе.

Воспользовавшись понятием когерентности, можно сказать, что когда t_{прибора}>>t_ког., то прибор не зафиксирует интерференцию. Если же t_{прибора}<<t_ког., то прибор (глаз, фотопластинка и пр.) обнаружит четкую интерференционную картину.

Соответственно, длиной когерентности называется расстояние , на которое перемещается волна за время t_ког.. Длина когерентности есть то расстояние, на котором случайное измерение фазы достигает значения ~. Для получения интерференционной картины путем деления естественной волны на две части необходимо, чтобы оптическая разность хода была меньше, чем длина когерентности. Это требование ограничивает число видимых интерференционных полос. С увеличением номера полосы “m” разность хода растет, поэтому четкость полос делается все хуже и хуже.

При интерференции немонохроматических волн время когерентности и длина когерентности определяются выражениями: и .

Пространственная когерентность.

П

Рис. 8

усть источник имеет угловые размеры  (рис.8). Если , то можно наблюдать интерференцию. Отсюда следует, что наибольшее расстояние, между щелями, при котором можно наблюдать интерференцию от источника с угловым размером , определяется из условия ;

Будем называть длиной пространственной когерентности или радиусом когерентности некое расстояние _ког., при смещении на которое вдоль некой волновой поверхности случайное изменение фазы достигает значения ~. . Для Солнца, например, ~0,01рад; ~0,5мкм  _ког.=0,05мкм. По мере удаления от источника степень пространственной когерентности возрастает.

Вследствие ограничений, накладываемых временной и пространственной когерентностями, интерференция при освещении тонкой пластинки наблюдается только в том случае, если толщина пластинки не превышает нескольких сотых долей миллиметра. При освещении светом с большой степенью когерентности интерференция наблюдается и при отражении от более толстых пластинок и пленок.

      

Рассмотрим теперь интерференцию монохроматического⁵ света при падении на пленку или пластинку расходящегося пучка лучей (например, при падении сферической волны).

В этом случае результаты интерференции отраженного (и проходящего) света в различных точках пластинки зависят от углов падения  лучей. Лучи, падающие под одинаковым углом ₁, создадут на экране совокупность одинаково освещенных точек, образующих криволинейную темную (или светлую) полосу. Каждой из этих полос соответствует определенное значение угла . Поэтому они называются полосами равного наклона. При нарушении плоскопараллельности пленки или пластинки форма полос равного наклона искажается. Этим используются при проверке качества шлифовки плоскопараллельных стеклянных пластин, причем обнаруживают отклонение от плоскопараллельности, равное 0,01мкм.

Справка 3.

- временная когерентность

Т.к. оптические разности хода для проходящего и и отраженного света отличаются на , максимум интерференции в отраженном свете будет соответствовать минимуму в проходящем и наоборот.

С увеличением толщины (d) плоскопараллельной пластины влияние угла наклона становится все менее заметным, полосы равного наклона становятся все ближе и ближе друг к другу. И при больших толщинах плоскопараллельных пластин интерференцию света в них наблюдать не удается.