21.Изгиб и растяжение (сжатие)

 На практике очень часто встречаются случаи совместной работы стержня на изгиб и на растяжение или сжатие. Подобного рода деформация может вызываться или совместным действием на балку продольных и поперечных сил, или только одними продольными силами.

Первый случай изображен на Рис.1. На балку АВ действуют равномерно распределенная нагрузка q и продольные сжимающие силы Р.

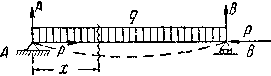
Рис.1 Совместное действие изгиба и сжатия.

 Предположим, что прогибами балки по сравнению с размерами поперечного сечения можно пренебречь; тогда с достаточной для практики степенью точности можно считать, что и после деформации силы Р будут вызывать лишь осевое сжатие балки.

Применяя способ сложения действия сил, мы можем найти нормальное напряжение в любой точке каждого поперечного сечения балки как алгебраическую сумму напряжений,вызванных силами Р и нагрузкой q.

Сжимающие напряжения от силР равномерно распределены по площади F поперечного сечения и одинаковы для всех сечений:

нормальные напряжения от изгиба в вертикальной плоскости в сечении с абсциссой х, которая отсчитана, скажем, от левого конца балки, выражаются формулой

Таким образом, полное напряжение в точке с координатой z (считая от нейтральной оси) для этого сечения равно

22. Сложное сопротивление. Общие понятия, назначение. Косой изгиб. Изгиб с кручением

Ранее были рассмотрены виды нагружения, при которых в сечениях элементов конструкций возникал только один внутренний силовой фактор: нормальная сила N - при растяжении, изгибающий момент М_х - при чистом изгибе, крутящий момент М_к - при кручении. Эти виды нагружения, растяжение, изгиб, кручение, являются простыми. 

Кроме простых видов нагружения бывают и сложные виды нагружения или иначе сложное сопротивление.

Сложным сопротивлением называются виды нагружения, при которых в поперечных сечениях одновременно действуют несколько внутренних силовых факторов.

Наиболее часто в расчетной практике встречаются следующие виды сложного сопротивления:

- косой изгиб;

-внецентренное растяжение;

-изгиб с кручением.

При расчете сложного сопротивления используется принцип независимости действия сил. Сложный вид нагружения представляется как система простых видов нагружения действующих независимо друг от друга. Решение при сложном сопротивлении получается в результате сложения решений полученных при простых видах нагружения.

23. Усталостная прочность. Общие понятия, назначение. Параметры циклов нагружения

Усталостная прочность - это прочность материала при циклическом нагружении. Усталостная прочность измеряется как и напряжение в [MПa]. Усталостная прочность обычно меньше в два или более раз чем предел прочности.

Частота нагружения. На воздухе частотные зависимости пороговой интенсивности напряжений различных материалов неоднозначны. При этом линейная зависимость параметра от частоты сохраняется для всех исследуемых форм циклов напряжений. Влияние повышенной температуры испытаний. Характерной особенностью роста усталостной трещины при повышенных температурах является независимость порогового размаха коэффициента интенсивности напряжения от температуры испытаний в условиях нагружения с высокой асимметрией цикла напряжений.

Циклом напряжений называется совокупность всех последовательных значений переменных напряжений за один период процесса их изменения.

Параметры циклов:Наибольшее (в алгебраическом смысле) напряжение цикла называется максимальным и обозначается (илиесли рассматривается изменение касательных напряжений), а наименьшее – минимальным(или).

Амплитудой (или переменной составляющей) называется алгебраическая полуразность максимального и минимального напряжений цикла .         Амплитуда цикла всегда положительна.

Цикл называют симметричным если напряжения иравны друг другу по абсолютной величине и обратны по знаку.Цикл называютасимметричным если напряжения ине равны друг другу по абсолютной величине.