33. Расчёт на прочность при растяжении и сжатии. Допускаемое напряжение и коэффициент запаса.

При проектировании элемента конструкции необходимо определить размеры, обеспечивающие его безопасную работу при заданных нагрузках. Для успешного решения этой задачи необходимо исходить из того, чтобы наибольшее расчётное напряжение в поперечном сечении элемента конструкции, возникшее при заданной нагрузке, было меньше того предельного напряжения, при котором возникает опасность появления пластической деформации или опасность разрушения.

Отношение предельного напряжения к расчётномуназывается коэффициентом запаса прочностиs:

.

При расчёте элемента конструкции коэффициент запаса прочности задаётся заранее и называется нормативным или требуемым и обозначается [s].

Прочность элемента конструкции обеспечивается, если действительный коэффициент запаса прочности не ниже требуемого т.е.

s>=[s]

Это неравенство выражает условие прочности элемента конструкции.

Разделив предельное напряжение на нормальный коэффициент запаса, получим допускаемое напряжение :

Тогда условие прочности можно выразить неравенством

т.е. прочность элемента конструкции обеспечивается, если наибольшее напряжение, возникающее в нём, не превышает допускаемого.

34. Чистый сдвиг. Напряжение и деформация при сдвиге.

Чистым сдвигом называется такой вид нагружения, когда на гранях параллелепипеда действует только касательное напряжение.

П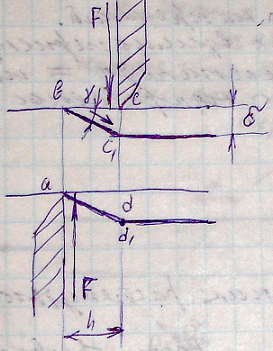од действием сил происходит деформация.

Происходит перемещение материала на величину .

- угол сдвига;

- перемещение;

h – расстояние действия сил.

Из

- назначается коэффициент запаса > 1.

35. Кручение бруса круглого, поперечного сечения. Напряжение и деформация при кручении. Определение максимальных касательных напряжений.

Под кручением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникает только крутящий момент. Прочие силовые факторы (изгибающие моменты, нормальная и поперечные силы) равны нулю.

Расчётная схема закрученного образца:

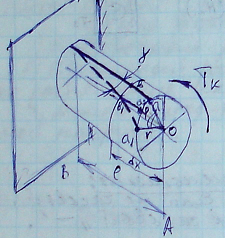
- полный угол закручивания.

Берём элементарный участок:

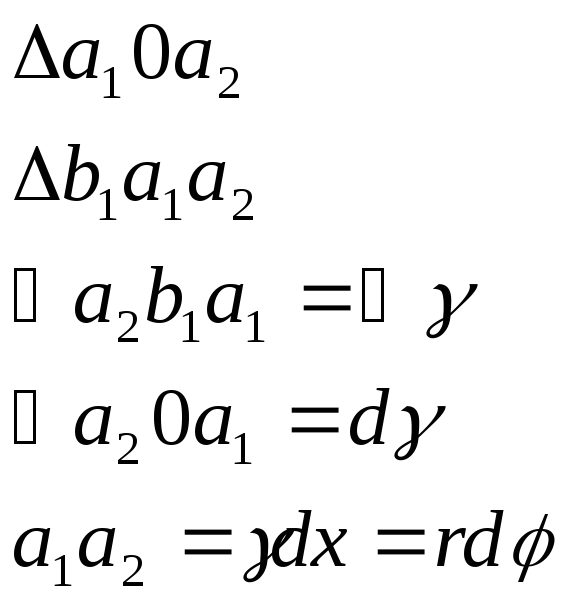
- относительный угол поворота, приходящийся на единицу длины.

зависит от радиуса поперечного сечения круглого стержня.

Внутренняя сила в точке К определяется

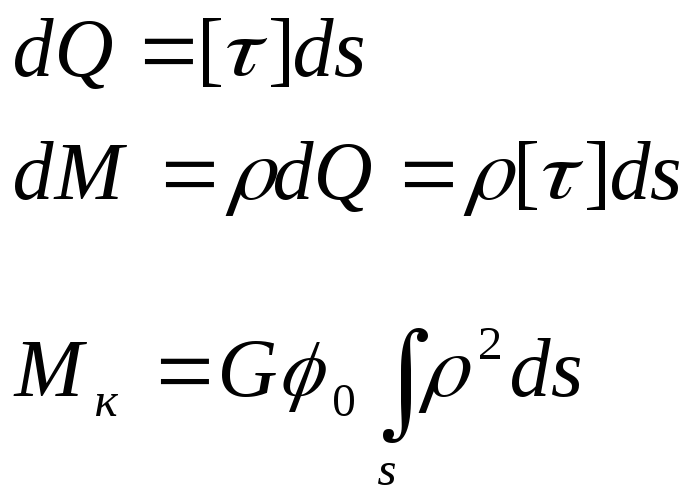
- полярный момент инерции поперечного сечения – геометрическая характеристика, зависящая от размеров поперечного сечения.

- зависимость при кручении.

36. Геометрические характеристики брусьев круглого, поперечного сечения при кручении. Потенциальная энергия деформации при кручении.

11) Расчёт валов на прочность и жёсткость при кручении.

Условие прочности при кручении

где - полярный момент сопротивления при кручении.

- допускаемое касательное напряжение.

n – коэффициент запаса.

Для проектируемого вала:

Из условий прочности на кручение определяем минимальный диаметр вала:

, мм

где = 10…20 МПа.

Берётся заниженное значение допускаемого напряжения т.к. определяется минимальный диаметр вала.

Расчёт на жесткость:

Упругие перемещения вала отрицательно влияют на работу связанных с ним деталей: подшипников, зубчатых колёс и т.п. От прогиба вала в зубчатом зацеплении возникает концентрация нагрузки по длине зуба.

Перемещение при кручении валов постоянного диаметра определяют по формуле

где - угол закручивания вала, рад;T – крутящий момент; G - модуль упругости при сдвиге; l – длина закручиваемого участка вала; - полярный момент инерции сечения вала.

Если вал ступенчатый и нагружен несколькими T, то угол определяют по участкам и затем суммируют.