37. Моменты инерции сечения. Вычисление моментов инерции брусьев прямоугольного и круглого сечения.

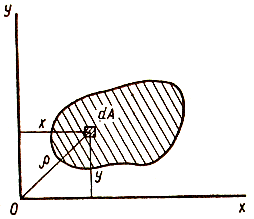
Представим, что сечение разделено на множество элементарных площадок dA (см. рис. – изображена одна из них), координаты которых x и y. Тогда интегралы

и

Называются моментами инерции сечения относительно осей x и y, а интеграл принято называть центробежным моментом инерции сечения относительно осейx и y.

Величина площади dA положительна, поэтому независимо от знака координаты x или y осевые моменты инерции всегда положительны, а центробежный момент инерции может быть как положительным, так и отрицательным в зависимости от расположения сечения относительно осей x или y.

Зависимость между осевыми и полярными моментами инерции

Сумма осевых моментов инерции сечения относительно взаимно перпендикулярных осей равна полярному моменту инерции относительно точки пересечения этих осей. Моменты инерции относительно осей, проходящих через центр тяжести сечения, называются центральными.

38.Прямоугольное сечение.

Прямоугольное сечение имеет две оси симметрии, а главные центральные оси Сx и Cy проходят через середины параллельных сторон.

Главный центральный момент инерции относительно оси x

Элементарную площадку dA в этом случае можно представить в виде полоски во всю ширину сечения и толщиной dy, значит dA=b*dy. Подставим под знак интеграла значение dA и проинтегрировав по всей площади, т.е. в пределах изменения ординаты y от –h/2 до +h/2, получим

Окончательно

Аналогично получим формулу главного центрального момента инерции прямоугольника относительно оси y:

39.Круглое сечение

Для круга главные центральные моменты инерции относительно осейx и y равны между собой.

Поэтому из равенства , получаем

или ,

где .

Подставим значение Jp и получим для круглого сечения

40. Изгиб брусьев. Внутренние силовые факторы в поперечных сечениях бруса и их эпюры. Дифференциальные зависимости при изгибе.

Под изгибом понимают такой вид нагружения, при котором в поперечных сечениях стержня возникают изгибающие моменты.

Все элементы конструкции подвергаются изгибу. Все элементы конструкции рассчитывают на изгиб, при этом принимают расчётную схему конструкции.

Балка – это брус, который воспринимает поперечные нагрузки и работает на изгиб.

Это наиболее распространённая схема для множества конструкций в технике – балка на 2х опорах.

Виды изгиба:

чистый;

- поперечный;

- прямой;

- косой.

Чистый изгиб – вид нагружения, когда в поперечном сечении балки действует только изгибающий момент.

Поперечный изгиб – когда на поперечное сечение действует одновременно изгибающий момент и поперечная сила (общий случай).

Пример чистого изгиба:- удельная нагрузка, приходящаяся на единицу длины конструкции.

Правило знаков поперечных сил при изгибе:

Правило знаков изгибающих моментов:

Правило проверки правильности построения эпюр нагружения:

В сечениях балки, где приложены внешние сосредоточенные нагрузки на эпюре д.б. скачёк на величину этой нагрузки.

Этапы:

1 Выбор расчётной схемы;

2 Анализ системы сил (система сил доводится до равновесного состояния);

3 Определение опорных реакций (ур-е статики) из условия равновесия;

4 Определение поперечных внутренних сил на каждом участке конструкции пользуясь методом сечения.