3.8. Методы построения векторных диаграмм

Одним из методов построения векторных диаграмм является метод, основанный на использовании промежуточных эквивалентных схем. На первом этапе построения векторной диаграммы, используется промежуточная эквивалентная схема, изображенная на рисунке 3.29, с последовательно соединенными элементами, и строится векторная диаграмма для последовательного соединения. А затем выделяется напряжение U₂₃ и строится диаграмма для параллельных ветвей и т.д.

Ниже приведен порядок построения векторной диаграммы разветвленной электрической цепи, приведенной на рисунке 3.34, в котором, на первом этапе строится векторная диаграмма параллельного участка.

1. Произвольно откладываем вектор напряжения U₂₃.

2. Строим векторную диаграмму токов:

   1. Откладываем вектор тока I₂. Он опережает напряжение U₂₃ на угол ₂ и режим работы активно-емкостной.

2. Откладываем вектор тока I₃. Он имеет активно-индуктивный характер и отстает от напряжения U₂₃ на угол ₃.

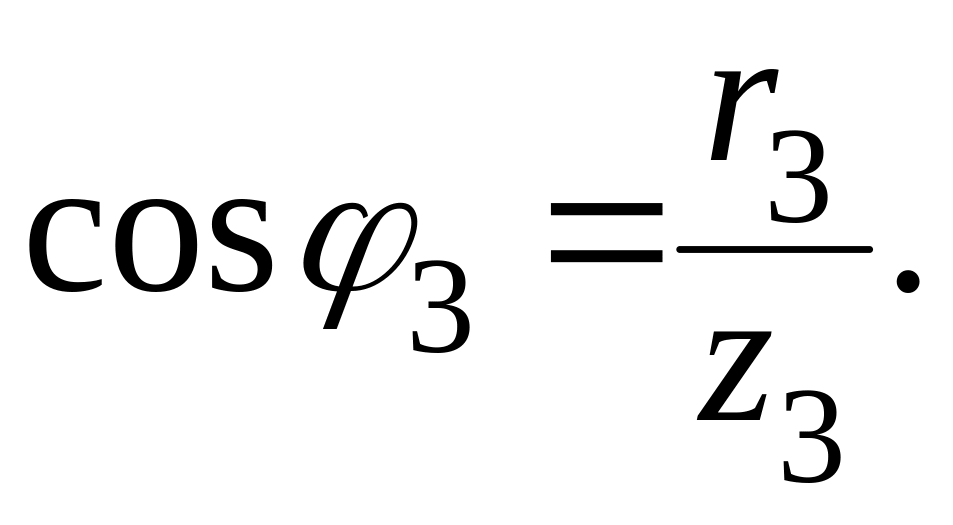
3. Откладываем вектор тока I₄. Он имеет чисто активный характер, поэтому совпадает с направлением напряжения U₂₃.

4. Строим вектор I₁. Его величина и направление определяется как векторная сумма токов I₂, I₃, I₄.

1. Откладываем вектор падения напряжения U_L1 на сопротивлении x_L1. Его величина равна U_L1 = I₁ x_L1. Он опережает ток I₁ на 90 и берет начало с точки 5, конец вектора соответствует точке 2 (рис. 3.35).

2. Откладываем вектор падения напряжения на сопротивлении r₁. Его величина равна U_r1 = I₁ r₁. Напряжение U_r1 совпадает с направлением тока I₁. Конец вектора совпадает с точкой 5, а начало соответствует точке 1 (рис. 3.35).

3. Откладываем вектор падения напряжения U_C1 на сопротивлении x_C1. Его величина равна U_C1 = I₁ x_C1. Он отстает от тока I₁ на 90 и берет начало с точки 3, конец вектора соответствует точке 4.

4. Определим вектор входного напряжения; для этого соединяем точки 1 и 4.

5. Откладываем векторы падений напряжений U_r2 и U_C2 на сопротивлениях r₂ и x_C2. Их величины равны U_r2 = I₂ r₂, U_C2 = I₂ x_C2. Направление векторов связано с направлением тока I₂.

6. Откладываем векторы падений напряжений U_r3 и U_L3 на сопротивлениях r₃ и x_L3. Их величины равны U_r3 = I₃ r₃, U_L3 = I₃ x_L3. Направление векторов связано с направлением тока I₃.

7. Откладываем вектор падения напряжения на сопротивлении r₄. Его величина равна U_r4 = U₂₃. Направление векторов связано с направлением тока I₄.

С помощью векторной диаграммы (рис. 3.35), можно определить напряжения между любыми точками схемы.

П ример 3.4. Рассмотрим порядок построения векторной диаграммы на примере 3.3., расчета электрической цепи, изображенной на рисунке 3.36.

1. Произвольно откладываем вектор напряжения (В).

2. Строим векторную диаграмму токов:

1. Откладываем вектор тока I₂ = 8 (A). Он опережает напряжение U₂₃ на угол ₂ и режим работы активно-емкостной.

.

2. Откладываем вектор тока I₃ = 6 (A). Он имеет активно-индуктивный характер и отстает от напряжения U₂₃ на угол ₃.

.

2. Строим вектор I₁ = 8,55 (A). Его величина и направление определяется как векторная сумма токов I₂ и I₃.

3. Откладываем вектор падения напряжения на сопротивлении r₂. Его величина равна (B). Это падение напряжения будет совпадать с направлением тока I₂. Конец вектора совпадает с точкой 3, начало соответствует точке 2, (рис. 3.37).

4. Откладываем вектор падения напряжения U_C2 на сопротивлении

x_C2. Его величина равна (В). Он отстает от тока I₂ на 90 и берет начало с точки 4, конец вектора соответствует точке 3.

2. Откладываем вектор падения напряжения на сопротивлении r₃. Его величина равна (B). Это падение напряжения будет совпадать с направлением тока I₃. Конец вектора совпадает с точкой 5, начало соответствует точке 2, (рис. 3.37).

3. Откладываем вектор падения напряжения U_L3 на сопротивлении x_L3. Его величина равна (B). Он опережает ток I₃ на 90 и берет начало с точки 5, конец вектора соответствует точке 3 (рис. 3.37).

4. Откладываем вектор падения напряжения на сопротивлении r₁. Его величина равна (В). Это падение напряжения будет совпадать с направлением тока I₁. Конец вектора совпадает с точкой 6, начало соответствует точке 2, (рис. 3.37).

5. Откладываем вектор падения напряжения U_C1 на сопротивлении x_C1. Его величина равна (В). Он отстает от тока I₁ на 90 и берет начало с точки 6, конец вектора соответствует точке 1 (рис. 3.37).

10. Откладываем вектор падения напряжения на сопротивлении r₄. Его величина равна (В). Это падение напряжения будет совпадать с направлением тока I₁. Конец вектора совпадает с точкой 7, начало соответствует точке 3 (рис. 3.37).

11. Откладываем вектор падения напряжения U_L4 на сопротивлении x_L4. Его величина равна (B). Он опережает ток I₁ на 90 и берет начало с точки 7, конец вектора соответствует точке 8 (рис. 3.37).

12. Определим вектор входного напряжения U; для этого соединяем точки 1 и 8.

Векторная диаграмма для рассматриваемого примера, изображена на рисунке 3.37.