3.12.5. Понятие о резонансе в сложных цепях
Условие резонанса
или
для разветвленной цепи с несколькими
индуктивными и емкостными элементами,
дают для частоты
уравнения, которые могут иметь несколько
вещественных корней, т.е. у разветвленной
цепи может быть несколько резонансных
частот.
Допустим, имеется
цепь, представленная на рис 3.85, потерями
в которой можно пренебречь. Входное
сопротивление данной цепи реактивное
и равно
.
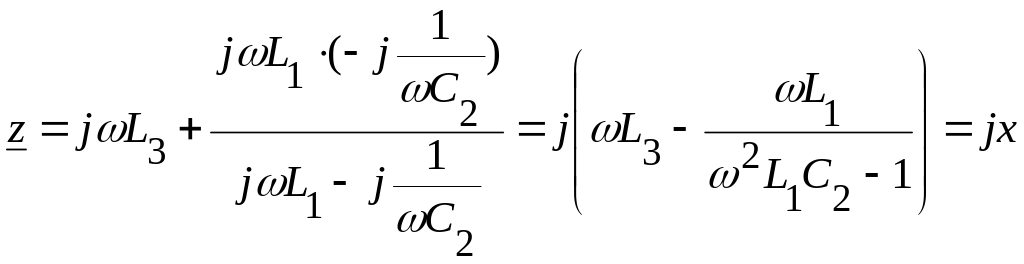Резонанс наступает
при
или
,
причем если
,
то
,
и, наоборот, если
,
то
.
Это справедливо всегда, если пренебречь
активными сопротивлениями в ветвях.
Следовательно, резонансными будут
частоты, обращающие
в нуль или в бесконечность. В рассматриваемом
случае
при
или
.
При этой частоте
наступает резонанс токов в параллельных
ветвях
и
.
Полагая
,
получаем
.
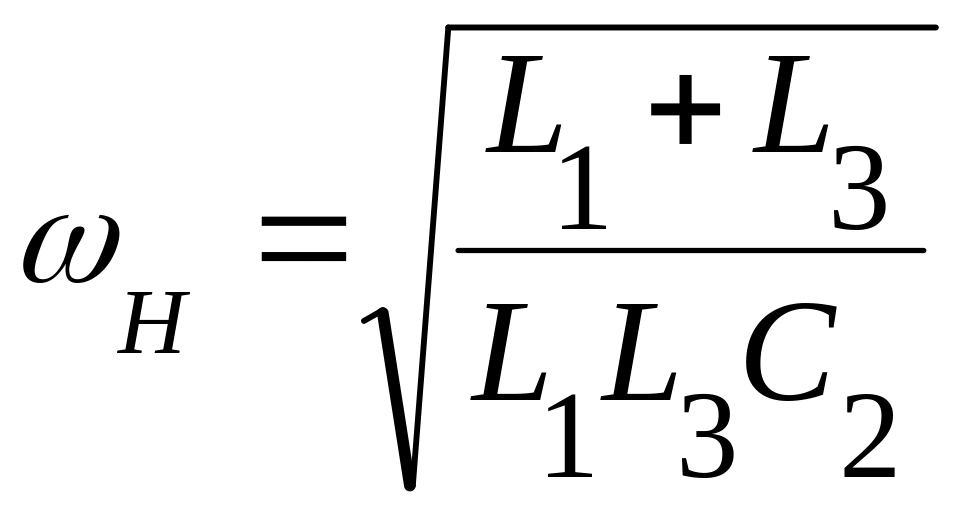При этой частоте
имеет место резонанс напряжений в
последовательном контуре, состоящем
из индуктивного и емкостного элементов,
эквивалентной схеме двум параллельным
ветвям. Таким образом, у рассматриваемой
цепи две резонансные частоты:
и
.
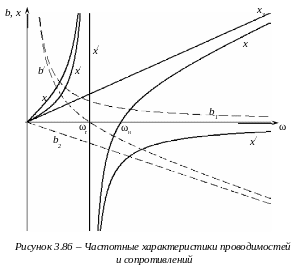
На рисунке 3.86,
приведены частотные характеристики
проводимостей и сопротивления
рассматриваемой цепи. Кривые
и
представляют характеристики проводимостей
ветвей 1 и 2. Суммируя ординаты этих
кривых, получаем характеристику
эквивалентной проводимости
двух параллельных ветвей. Кривая
представляет эквивалентное сопротивление
параллельных ветвей. Суммируя ординаты
кривых
и
,
построим характеристику входного
сопротивления цепи
.
Эта характеристика имеет две особые
точки
и
.
3