1.3 Средние величины: средняя, средневзвешенная, мода Мо, медиана Ме. Показатели вариации: дисперсия, среднее квадратическое отклонение, коэффициент вариации.

Среднее значение (иногда называемое показателем позиции или показателем центра) является наиболее важным специальным статистическим показателем, используемым для обобщения данных. Среднее значение дает представление о наиболее «типичном» или «центральном» значении в интервале изменения пере­менной. Часто опубликованные материалы, например отчеты предприятий, со­держат средние значения различных переменных. Например, средняя заработная плата, средний объем выпуска, средняя Продолжительность рабочей недели и сред­ний объем продаж — все эти термины часто встречаются в той или иной форме. При рассмотрении такого рода статистических показателей особое внимание сле­дует уделить точному выяснению методики расчета указанных средних. Имеется несколько таких методов, и каждый из них зачастую дает различные результаты. В данном разделе описаны три наиболее часто используемые в большинстве практи­ческих ситуаций «средние».

Определение. Средняя — это статистический показатель «середины» или «центра» исследуемых данных.

Средняя арифметическая

Средняя арифметическая, или, обычно, просто средняя, используется наи­более часто для определения среднего значения. Более того, для многих людей средняя — это единственное рассматриваемое значение. Основное достоинство использования данного показателя состоит в наличии стандартной математи­ческой формулы. Данный факт, по крайней мере, обеспечивает объективность полученных значений. Далее приведены несколько примеров расчета средней арифметической.

Определение. Средняя арифметическая получается путем деления суммы всех значений на их количество.

Пример 1

Недельный доход каждого из пяти работников составляет соответственно: 400, 350, 520, 440 и 490 ф. ст.

Средняя арифметическая этих значений получается путем деления суммы значений на их количество. Таким образом,

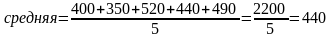
Следовательно, средний недельный доход для данной группы работников составляет 440 ф. ст. В общем виде, при n значениях x среднее рассчитывается по формуле

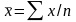
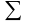(буква греческого алфавита «сигма») означает «сумма». Таким образом, формула читается как сумма х, деленная на n. При наличии таблицы частот, средняя рассчитывается по следующей формуле:

Рассмотрим приведенную ниже таблицу частот, содержащую данные невы­ходов на работу за последние 20 дней.

Количество отсутствовавших : 1 2 3 4 5

Количество дней отсутствия 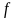: 4 7 5 2 2

Среднее значение количества отсутствовавших в день рассчитывается путем деления суммы значений на количество дней. В данной таблице отмечено 4 дня, когда было только по одному отсутствовавшему, 7 дней — по 2 и т. д.

.

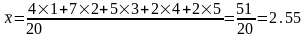Мода

Средняя набора значений может быть получена путем определения моды. Моду можно коротко определить как значение, наиболее часто встречающе­еся в наборе данных. Это наиболее «типичное» значение среди данных, и часто его считают более репрезентативным, т.е. более достоверным, нежели среднюю арифметическую. На последующих примерах мы рассмотрим поря­док получения моды на основании данных, представленных в том или ином виде.

Определение. Мода — это средняя, получаемая путем установления наибо­лее часто встречающегося значения в наборе данных.

Пример. Нижеприведенные значения показывают количество работников, отсут­ствовавших на работе за период в 10 дней:

3, 5, 2, 1, 4, 3, 2, 0, 3, 6

Здесь видно, что наиболее часто встречается цифра 3. Отсюда мода равня­ется 3 работникам. Таким образом, среднее количество работников, отсутство­вавших на работе, можно определить как равное 3.

Пример. В таблице приведено количество отсутствовавших на работе за последние три недели (21 день):

Количество отсутствовавших: 0 1 2 3 4

Количество дней 2 8 6 3 2

Из таблицы частот следует, что чаще всего (8 дней) отсутствовало по одному работнику.

Таким образом, мода равняется 1 работнику. Как видно на примере такой простой таблицы частот, определение моды не представляет труда. Мы просто находим и соотносим ее со значением соответствующей пере­менной. Однако если таблица частот содержит интервалы группировки, то процесс определения становится более сложным.

Медиана

Еще один способ определения среднего значения набора данных заключа­ется в получении медианы. В ряде случаев это наиболее приемлемый и очевидный вариант выявления центрального значения. В буквальном смысле, медиана — это срединное значение при условии, что данные выстроены в ранжирован­ном порядке. На последующих примерах вы познакомитесь со способом опреде­ления медианы.

Определение. Медиана — это среднее, полученное путем выявления «цент­рального» значения в перечне данных, расположенных в ранжированном порядке.

Пример.

Рассмотрим таблицу частот, отображающую количество невыходов на ра­боту за период в три недели (21 день):

Количество отсутствовавших: 01234

Количество дней: 2 8 6 3 2

Согласно данной таблице, общее количество дней равно n =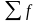 = 21.

Отсюда медиана = [(n + 1)/2]-е или [(21 + 1)/2]-е = 11-е значение.

Теперь необходимо из этих данных выбрать 11-е значение. Есть 2 дня, в которые не отмечено невыходов; есть 8 дней, в которые отмечено по 1 невы­ходу. Следовательно, первые десять значений — это 0 или 1. Таким образом, 11-е значение — это 2. Итак, медиана равна 2-м работникам.

Дисперсия

Иногда значение дисперсии приводится как мера вариации вместо среднеквадратического отклонения. Это значение — просто квадрат среднеквадратического отклонения. Так, его можно получить по следующей формуле:

Дисперсию можно использовать при проведении сложного анализа при объединении различных наборов данных. Значения дисперсии могут быть объе­динены напрямую, а значения среднеквадратического отклонения — нет.

Однако достоинство среднеквадратического отклонения состоит в том, что оно дается в единицах измерения анализируемой переменной, например в ф. ст., если мы рассматриваем доход или заработную плату. Обычно, в большинстве случаев, предпочтение отдается среднеквадратическому отклонению.

Определение. Дисперсия — это мера вариации, получаемая путем возведе­ния в квадрат среднеквадратического отклонения.

Среднеквадратическое отклонение

Одной из наиболее важных характеристик вариации является значение среднеквадратического отклонения, обычно обозначаемое 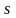или 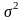. Основное достоинство среднеквадратического отклонения состоит в том, что его можно рассчитать с помощью объективной математической формулы, а не путем оце­ночных методов, как в случае с межквартильным размахом. Среднеквадратичес­кое отклонение выборки значений можно рассчитать по следующей формуле:

Среднеквадратическое отклонение .

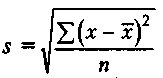Как вариант, Среднеквадратическое отклонение может быть рассчитано на основании данных таблиц частот с помощью одной из следующих формул:

Среднеквадратическое отклонение

Определение. Среднеквадратическое отклонение есть мера вариации, полу­чаемая путем извлечения квадратного корня из средней суммы квадратов откло­нений между каждым значением и арифметической средней.

Коэффициент вариации

При рассмотрении различных распределений с существенно отличными значениями арифметической средней для проведения более реалистичного сравнения применяется коэффициент вариации. Например, распределение с большим значением арифметической средней, вероятно, даст большую ва­риацию. То есть, базовое сравнение вариации с помощью среднеквадрати­ческого отклонения или квартилей может и не дать какой-либо дополни­тельной информации. Коэффициент вариации позволяет сравнить вариацию относительно величины рассматриваемых данных. Значение получается сле­дующим образом:

О

пределение. Коэффициент вариации — это особый показатель вариации, получаемый путем соотношения среднеквадратического отклонения и арифмети­ческой средней и выражаемый в процентах.

Полученное значение дает среднеквадратическое отклонение в процентах от арифметической средней. Например, рассмотрим следующие наборы данных:

Таблица показывает, что среднее значение Б больше среднего значения А. Кроме того, разброс данных Б больше, чем разброс данных А. Однако когда мы рассчитаем коэффициент вариации для каждого набора данных, нам предста­нет иная картина: ;

Данные А: коэффициент вариации = 50/200 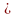100 = 25%.

Данные Б: коэффициент вариации — 60/300 100 = 20%.

Анализ показывает, что при соотнесении со средними значениями вариа­ция в Б меньше, чем в А.

Следует отметить, что в отличие от других значений, представленных в данном разделе, коэффициент вариации не является «овеществленной» мерой разброса. Например, при рассмотрении заработной платы большинство показа­телей выражены в используемой денежной единице, скажем, в фунтах стерлин­гов. В противоположность этому коэффициент вариации не зависит от исполь­зуемой единицы измерения.

11. Классическое определение вероятности.

Вероятность события – это оценка шансов наступления события.

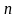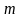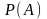Если число – число всех исходов испытания, а – число исходов, благоприятствующих событию А, то вероятность наступления события 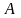находится по формуле:

.

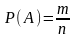Свойства вероятности.

• 1. Вероятность достоверного события равна 1.

.

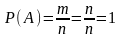• 2. Вероятность невозможного события равна 0.

.

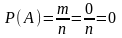• 3. Вероятность события удовлетворяет неравенству:

.

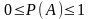12. Приведите примеры случайных событий в экономике. Можно ли дать им вероятностное описание?

Под событием понимается явление, которое происходит, в результате осуществления какого-либо определённого комплекса условий будем называть опытом или испытанием.

Определение. Случайным называется событие, которое может произойти или не произойти в результате некоторого испытания (опыта).

События обычно обозначают заглавными буквами латинского алфавита A,B,C,…и т.д.

13. Приведите примеры совместных и несовместных событий.

Определение. События A и В называются несовместными, если в результате данного испытания появление одного из них исключает появления другого.

Определение. События A и В называются совместными, если в результате данного испытания появление одного из них не исключает появления другого.

Пример. Появление на верхней грани кубика трёх очков исключает появление шести очков, при одном испытании – несовместное событие.

Пример. Выпадение четного числа очков и выпадение числа очков, равного 6 – совместное событие.