
- •Как вычисляются основные числовые характеристики по результатам выборки: «группа средних». Объяснить на примерах.
- •1.3 Средние величины: средняя, средневзвешенная, мода Мо, медиана Ме. Показатели вариации: дисперсия, среднее квадратическое отклонение, коэффициент вариации.
- •14. Приведите примеры зависимых и независимых событий
- •16. Дайте возможные определения вероятности. Приведите примеры их использования.
- •17. Что такое относительная частота события, как она связана с вероятностью?
- •18. Что такое случайная величина (св)? Какие виды св известны?
- •26. В каких случаях применяют формулу Байеса? (Показать на примерах)
- •27. В каких случаях применяют формулу Бернулли? (Показать на примерах)
- •§ 1. Испытания Бернулли.
- •§ 2. Наивероятнейшее число успехов.
- •Если число np-q - дробное, то существует одно наивероятнейшее число m*;
- •Если число np-q - целое, то существует два наивероятнейших числа
- •28. В каких случаях применяют формулу Пуассона? (Показать на примерах)
- •29. Что такое функция распределения св? Что такое плотность вероятности св? Приведите ее свойства.
- •30. Как рассчитывается вероятность попадания св в определенный интервал с помощью функции распределения, с помощью плотности вероятности?
- •36 Что такое дерево вероятностей? Сформулируйте правила построения и проверки корректности дерева вероятностей?
- •37. Какая выборка называется репрезентативной? Каким образом можно извлечь репрезентативную выборку?
- •38. Какой интервал мы называем доверительным?
- •39 Что называется уровнем доверительности (confidence level)?
- •40. Какой из двух доверительных интервалов больше: двусторонний 99% или двусторонний 95%? Объясните.
1. Определите какие основные разделы математики представляют количественные методы в бизнесе?
Финансовая математика, эконометрика, высшая математика, теория вероятностей.
2.Каково значение анализа данных при принятии управленческих решений?
Для современного руководителя всё большую значимость приобретает применение основных методов представления и пояснения коммерческой информации, которые лежат в основе формирования имиджа и маркетинговой стратегии многих предприятий. Методы представления данных способствуют лучшему пониманию. Качественная информация порождает правильные решения.
Это схема иллюстрирует значение анализа данных при принятии управленческих решений. Точное и эффективное использование данных играет важную роль в жизни современных предприятий и их руководителей. Правильно отобранные и проанализированные первичные данные лежат в основе принятия управленческих решений и таким образом способствуют повышению качества работы и конкурентоспособности организации. К методам анализа данных относится сведение первичных данных в таблицы и графическое представление информации. Данные, собранные в ходе обследований, анкетирования, опросов, наблюдения или из печатных источников, могут анализироваться многими способами. К методам первичного анализа данных относится составление таблиц частот (дискретных и интервальных вариационных рядов) на основе исходных данных, а также соответствующих графиков, таких как гистограммы, столбиковые диаграммы, линейные графики или секторные диаграммы. Анализу подвергаются показатели рентабельности, доходы, расходы и объем производства. Для проведения такого рода анализа можно использовать методы анализа данных. Первый этап любого количественного анализа состоит в сборе необходимой информации. Для проведения сбора данных существует множество методов: анкетирование, опрос, наблюдение или обращение к имеющимся данным.
3.Что такое генеральная совокупность и выборка? Приведите примеры.
Совокупность, из которой производится отбор, называется генеральной, и все её обобщающие показатели - генеральными. Совокупность отобранных единиц именуют выборочной совокупностью, и все её обобщающие показатели - выборочными.
Так называемая «генеральная совокупность» включает в себя всех индивидуумов, которые, вероятно, могли бы быть охвачены в ходе проведения исследования. Очертить конкретную (выборочную) совокупность не всегда просто, как это кажется на первый взгляд. Возьмем, к примеру, анализ условий труда и вознаграждения работников. Вполне возможно, что искомая совокупность охватывает всех работников, а может быть, только работников определенного уровня или работающих на конкретном месте. Кроме того, можно расширить рамки совокупности за счет охвата потенциальных работников, например взрослого населения определенной местности, имеющего соответствующие навыки и умения.
Основа выбора используется для выделения представительной выборки из уже определенной совокупности. В отношении всех работников такой основой может служить обычная система учета работников. Также в качестве основы можно использовать, например, списки членов профессиональных организаций, клубных учреждений, а возможно, и телефонные справочники или даже списки избирателей. Основа выбора является важным элементом всего процесса и, будучи неверно определенной, способна существенным образом повлиять на пригодность собранной информации. Например, если мы хотим охватить все домашние хозяйства, то телефонный справочник в этом случае не может служить полностью корректной основой. Более того, она, вероятно, наведет нас на неверные выводы, даже если мы ставим целью охватить только телефонизированные домашние хозяйства, так как небольшая часть таких хозяйств не фигурирует в справочнике.
Объем выборки. Количество собранной информации зависит от различных факторов, в том числе использованных методов сбора данных, имеющихся средств, конкретной исследуемой совокупности и требуемой точности результатов. В целом, при условии объективности выборки увеличение объема выборки скорее всего, повысит надежность полученных результатов.
4.Что такое статистический ряд? Что такое интервальный статистический ряд?
Результаты сводки и группировки материалов статистического наблюдения
оформляются в виде статистических рядов распределения. Статистические
ряды распределения представляют собой упорядоченное распределение
единиц изучаемой совокупности на группы по группировочному
(варьирующему) признаку. Они характеризуют состав (структуру)
изучаемого явления, позволяют судить об однородности совокупности,
границах ее изменения, закономерностях развития наблюдаемого объекта. В
зависимости от признака статистические ряды распределения делятся на:
- атрибутивные (качественные);
- вариационные (количественные)
а) дискретные;
б) интервальные;
Интервальный статистический ряд строится для непрерывных случайных величин и для дискретных случайных величин с большим числом вариант.
Пусть
![]() –
интервал возможных значений случайной
величины
–
интервал возможных значений случайной
величины
![]() ,
в частности
,
в частности
![]() .Этот
интервал разбивают на частичные интервалы
.Этот
интервал разбивают на частичные интервалы
![]() и
подсчитывают количество значений из
выборочных совокупностей (1), принадлежащих
каждому частичному интервалу
и
подсчитывают количество значений из
выборочных совокупностей (1), принадлежащих
каждому частичному интервалу
![]() .
Затем составляют таблицу, в верхней
строчке которой указаны частичные
интервалы, а в нижней – соответствующие
им частоты. Полученную таблицу называют
интервальным статистическим рядом
кратностей (относительных частот). Для
графического изображения интервального
статистического ряда используют
гистограмму. Для этого на оси абсцисс
отмечают частичные интервалы, над каждым
из которых строится отрезок (горизонтальный)
с ординатой
.
Затем составляют таблицу, в верхней
строчке которой указаны частичные
интервалы, а в нижней – соответствующие
им частоты. Полученную таблицу называют
интервальным статистическим рядом
кратностей (относительных частот). Для
графического изображения интервального
статистического ряда используют
гистограмму. Для этого на оси абсцисс
отмечают частичные интервалы, над каждым
из которых строится отрезок (горизонтальный)
с ординатой
5.Дайте определение эмпирической функции распределения, приведите ее аналитическое и графическое представление.
Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения х относительную частоту события Х
F*(x)=nх/n
где nх – число вариант, меньшее х, n – объем выборки
Таким образом, для того, чтобы найти, например F*(x2), надо число вариант, меньшее x2, разделить на объем выборки n: F*(x2)=nх2/n
В отличие от эмпирической функции распределения выборки, интегральную функцию F(x) распределения генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F(x) определяет вероятность события Х
Из определения функции F*(x) вытекают следующие ее свойства: 1. Значения эмпирической функции принадлежат отрезку [0;1] 2. F*(x) - неубывающая функция 3. Если х1 – наименьшая варианта, то F*(x)=0 при х≤х1; если хk – наибольшая варианта, то F*(x)=1 при х>хk.
Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.
Пример 5. Построить эмпирическую функцию по данному распределению выборки:
Варианты |
xi |
2 |
6 |
10 |
Частоты |
ni |
12 |
18 |
30 |
Решение: Найдем объем
выборки: 12+18+30=60. Наименьшая варианта
равна 2, следовательно F*(x)=0 при x≤2.
Значение х<6, а именно х1=
2 наблюдалось 12 раз, следовательно,
F*(x)=12/60=0.2 при 21=2
и х2=6
наблюдались 12+18=30 раз, следовательно,
F*(x)=30/60=0.5 при 6
Так как х=10 – наибольшая
варианта, то F*(x)=1 при x>10.
Эмпирической
функцией распределения
![]() называется
функция
называется
функция
![]() ,
вычисляемая по выборке
,
вычисляемая по выборке
![]() следующим
образом:
следующим
образом:
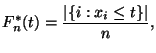
то
есть,
есть
отношение числа элементов выборки, не
превосходящих ![]() ,
к объему выборки. Слово ``эмпирическая''
в Определении 6.1
означает, что функция вычисляется по
данным опыта (эмпирическим данным), то
есть, по выборке. По этой же причине для
этого понятия иногда употребляют термин
выборочная функция распределения.
Cледует заметить, что F*(x)=0 при
x<X0 и F*(x)=1 при x>Xk.
Построив точки Mi [Xi
; F*(Xi)] и соединив их
плавной кривой, получим приближенный
график эмпирической функции распределения
(рис.
15). Используя закон больших
чисел Бернулли, можно доказать, что при
достаточно большом числе n испытаний
с вероятностью, близкой к единице,
эмпирическая функция распределения
F*(x) отличается сколь угодно мало от
неизвестной нам функции распределения
F(x) cлучайной величины
,
к объему выборки. Слово ``эмпирическая''
в Определении 6.1
означает, что функция вычисляется по
данным опыта (эмпирическим данным), то
есть, по выборке. По этой же причине для
этого понятия иногда употребляют термин
выборочная функция распределения.
Cледует заметить, что F*(x)=0 при
x<X0 и F*(x)=1 при x>Xk.
Построив точки Mi [Xi
; F*(Xi)] и соединив их
плавной кривой, получим приближенный
график эмпирической функции распределения
(рис.
15). Используя закон больших
чисел Бернулли, можно доказать, что при
достаточно большом числе n испытаний
с вероятностью, близкой к единице,
эмпирическая функция распределения
F*(x) отличается сколь угодно мало от
неизвестной нам функции распределения
F(x) cлучайной величины
![]()
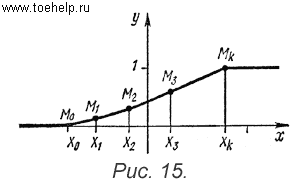
Часто вместо построения
графика эмпирической функции распределения
поступают следующим образом. На оси
абсцисс откладывают интервалы ] X0,
X1 [, ] X1, X2
[, ..., ] Xk-1, Xk
[. На каждом интервале строят
прямоугольник, площадь которого равна
частоте
![]() ,
соответствующей данному интервалу.
Высота hi этого прямоугольника
равна
,
соответствующей данному интервалу.
Высота hi этого прямоугольника
равна
![]() ,
где
,
где
![]() -
длинна каждого из интервалов. Ясно, что
сумма площадей всех построенных
прямоугольников равна единице.
Рассмотрим функцию
-
длинна каждого из интервалов. Ясно, что
сумма площадей всех построенных
прямоугольников равна единице.
Рассмотрим функцию
![]() ,
которая в интервале ] Xi-1,
Xi [ постоянна и равна
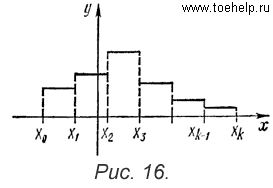
hi. График этой функции
называется гистограммой. Он
представляет собой ступенчатую линию
(рис.
16). С помощью закона больших
чисел Бернулли можно доказать, что при
малых
и
больших n с практической достоверностью
,
которая в интервале ] Xi-1,
Xi [ постоянна и равна
hi. График этой функции
называется гистограммой. Он
представляет собой ступенчатую линию
(рис.
16). С помощью закона больших
чисел Бернулли можно доказать, что при
малых
и
больших n с практической достоверностью
![]() как
угодно мало отличается от плотности
распределения
как
угодно мало отличается от плотности
распределения
![]() непрерывной
случайной величины
.
непрерывной
случайной величины
.
Что такое полигон частот и гистограмма? Для чего они используются?
Полигон и гистограмма
Для наглядности строят различные графики статистического распределения, в частности, полигон и гистограмму.
Полигоном частот называют
ломаную линию, отрезки которой соединяют
точки
![]() .
Для построения полигона частот на оси
абсцисс откладывают варианты
.
Для построения полигона частот на оси
абсцисс откладывают варианты
![]() ,
а на оси ординат – соответствующие им
частоты
,
а на оси ординат – соответствующие им
частоты
![]() и
соединяют точки
и
соединяют точки
![]() отрезками
прямых.
отрезками
прямых.
Полигон относительных
частот строится аналогично, за исключением
того, что на оси ординат откладываются
относительные частоты
![]() .
.
В случае непрерывного признака строится гистограмма, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала – сумму частот вариант, попавших в i–й интервал.
Гистограммой частот называют
ступенчатую фигуру, состоящую из
прямоугольников, основаниями которой
служат частичные интервалы длиною h, а
высоты равны отношению
![]() .
Для построения гистограммы частот на
оси абсцисс откладывают частичные
интервалы, а над ними проводят отрезки,
параллельные оси абсцисс на расстоянии
(высоте)
.
Площадь i–го прямоугольника равна
.
Для построения гистограммы частот на
оси абсцисс откладывают частичные
интервалы, а над ними проводят отрезки,
параллельные оси абсцисс на расстоянии
(высоте)
.
Площадь i–го прямоугольника равна
![]() –
сумме частот вариант i–о интервала,
поэтому площадь гистограммы частот
равна сумме всех частот, т.е. объему
выборки.
–
сумме частот вариант i–о интервала,
поэтому площадь гистограммы частот
равна сумме всех частот, т.е. объему
выборки.
В случае гистограммы
относительных частот по оси ординат
откладываются относительные частоты
,
на оси абсцисс – частичные интервалы,
над ними проводят отрезки, параллельные
оси абсцисс на высоте
![]() .
Площадь i–го прямоугольника равна
относительной частоте вариант
.
Площадь i–го прямоугольника равна
относительной частоте вариант
![]() ,
попавших в i–й интервал. Поэтому площадь
гистограммы относительных частот равна
сумме всех относительных частот, то
есть единице.
,
попавших в i–й интервал. Поэтому площадь
гистограммы относительных частот равна
сумме всех относительных частот, то
есть единице.
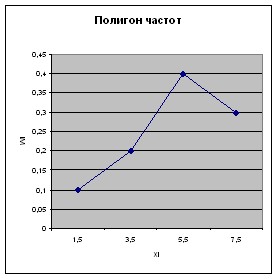
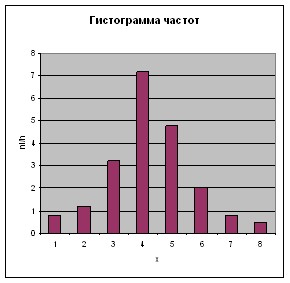
Полигон частот дает приближенное наглядное представление о характере распре-деления случайной величины х. Гистограмма используется для графического представления распределений непрерывно варьирующих признаков и состоит из примыкающих друг к другу прямоугольников. Основание каждого прямоугольника равно ширине интервала группировки, а высота его такова, что площадь прямоугольника пропорциональна частоте попадания в данный интервал.
Как вычисляются основные числовые характеристики по результатам выборки: «группа средних». Объяснить на примерах.
группа средних |
|
|
|
||||
|
|
хср |
Мо |
Ме |
|||
|
интервал.ряд |
131.2 |
133.9 |
133.9 |
|||
|
описат.стат |
131.7 |
145 |
134.5 |
|||
|
|
|
|
|
|||
**** Остальное в 10 вопросе
Как вычисляются основные числовые характеристики по результатам выборки: «меры вариации». Объяснить на примерах.
меры вариации |
|
|
|
|
|
||||||
|
хmax-xmin ( размах вариации) |
IQR (межкварт. размах) |
s2 (дисперсия) |
s (сред.квад. откл.) |
V(x) (вариации) |
|
|||||
интервал.ряд |
62.0 |
17.7 |
202.5 |
14.2 |
10.8% |
|
|||||
описат.стат |
62.0 |
19.5 |
209.5 |
14.5 |
11.0% |
|
|||||
|
|
|
|
|
|
|
|||||
КВАРТИЛЬ 1 |
125.0 |
123.25 |
|
|
|
||||||
КВАРТИЛЬ 3 |
142.7 |
142.75 |
|
|
|
||||||
Размах вариации
Размах вариации — это самая простая мера разброса набора данных. Размах вариации — промежуток между наибольшим и наименьшим значениями распределения. На последующих примерах вы познакомитесь с порядком расчета размаха вариации.
Определение. Размах вариации — это простая мера вариации, вычисляемая путем вычитания наименьшего значения в наборе данных из наибольшего.
Пример. Найдем размах вариации на основании значений недельного дохода небольшого розничного предприятия за последние десять недель. (Данные приведены в тыс. ф. ст.)
12, 20, 15, 8, 5, 14, 22, 13, 10, 17.
Чтобы получить размах вариации, необходимо найти наибольшее и наименьшее значения в последовательности данных. Таковыми в данном примере являются цифры 22 (максимальное значение) и 5 (минимальное значение). Следовательно, размах вариации рассчитывается следующим образом:
Размах вариации = 22 — 5 = 17. Таким образом, для этих данных размах вариации составляет 17 000 ф. ст.
***Остальное в 9 и 10 вопросе
9.Что показывает и как находится межквартильный размах?
Межквартильный размах
Размах, описанный в предыдущем разделе, имеет ряд недостатков. В целом, размах нельзя удовлетворительно применять при сравнении наборов данных, так как он может быть легко искажен экстремальными отдельными значениями. Например, в следующей таблице приведены данные по недельной заработной плате 100 работников предприятий А и Б соответственно:
Недельная заработная
плата (ф. ст.): 200- 300- 400- 500- 600- 700- 800- 900-
Количество
работников: предпр. А: 25 38 23 13 0 0 0 1
предпр. Б: 25 38 23 14 0 0 0 0
Размах для каждого набора данных составляет соответственно:
для предприятия А размах = 1000 — 200 = 800 ф. ст. для предприятия Б размах = 600 — 200 = 400 ф. ст.
Как видно, вариация согласно размаху для предприятия А в два раза больше вариации для предприятия Б. Однако при исследовании исходных таблиц частот эту разницу можно отнести на счет единственного работника, получающего в интервале 900—1000, в сравнении с еще одним работником предприятия Б, получающим в интервале 500—600. Таким образом, одно экстремальное значение полностью исказило значение размаха. Поэтому на этот размах не стоит полагаться при проведении приемлемого сравнения наборов данных. Следовательно, требуется альтернативный способ определения величины вариации. Для этих целей приемлемой величиной считается значение межквартильного размаха. Межквартильный размах получают путем исключительного рассмотрения «размаха» для центральных 50% значений набора данных. На рис. 1.21 представлено распределение набора данных. Если мы опустим 25% наименьших значений и 25% наибольших, тогда мы получим, как это показано на рисунке, размах, включающий центральные 50% значений, т. е. межквартильный размах. Два крайних значения из центральных 50% называются квартилями. Межквартильный размах (IQR) - расстояние между меньшей квартилью (Q,) и большей квартилью (Q3), как это показано на рисунке. Квартили можно подучить во многом аналогично тому, как мы определяли медиану ранее. Ведь медиа — это середина распределения и является [(n + 1)/2]-м порядковым значением.
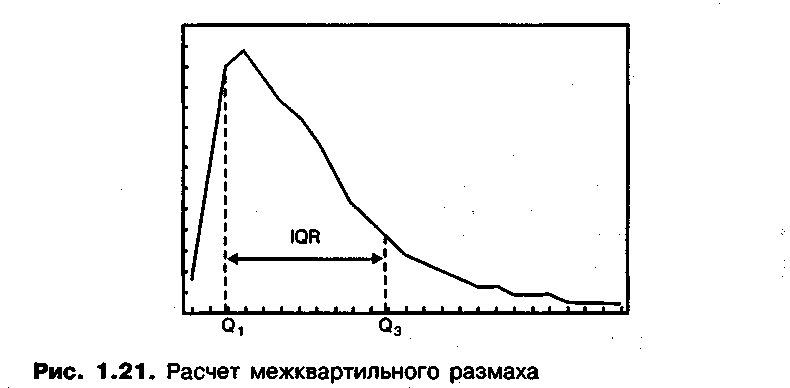
Аналогично, меньшая квартиль находится на расстоянии в 1/4 от начала распределения, а большая квартиль — на расстоянии в 3/4. Таким образом, эти квартили можно рассчитать следующим образом:
Меньшая квартиль, Q1 =
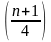 -е
порядковое значение;
-е
порядковое значение;
Большая квартиль, Q3 =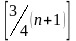 -е
порядковое значение. Имея эти значения,
получаем межквартильный размах:
-е
порядковое значение. Имея эти значения,
получаем межквартильный размах:
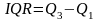 .
.
Определение. Межквартильный размах — это разница между большей и меньшей квартилями. Данное значение показывает размах для центральных 50% данныx.
10. О чем говорят числовые характеристики по результатам выборки: выборочные среднее, дисперсия, среднее квадратическое отклонение, коэффициент вариации?
