Лабораторна робота №11

Тема: " Метод сполученого градієнта Флетчера-Рівса"

(2 Години)

Ціль роботи: вивчення метода сполученого градієнта Флетчера–Рівса для знаходження мінімуму функції декількох змінних.

Теоретичні відомості:

Спряженість і сполучені напрямки.

Квадратична цільова функція n незалежних змінних, що має мінімум (позитивно визначена матриця Гесе), може бути мінімізована за n кроків (або менш), якщо ці кроки роблять у сполучених напрямках.

Система n лінійно-незалежних напрямків пошуку називається сполученої стосовно деякої позитивно певній (квадратної) матриці Q , якщо

.

Розглянемо квадратичну апроксимацію цільової функції f(x) – розкладання в ряд Тейлора, відкинувши всі члени розкладання третього порядку й вище

,

де

f(x) - апроксимуюча функція змінної x у крапці ;

;

- одиничний вектор у напрямку .

.

При визначенні крапки функція f(x) може бути мінімізована шляхом обчислення  з рівняння

.

,

тоді

.

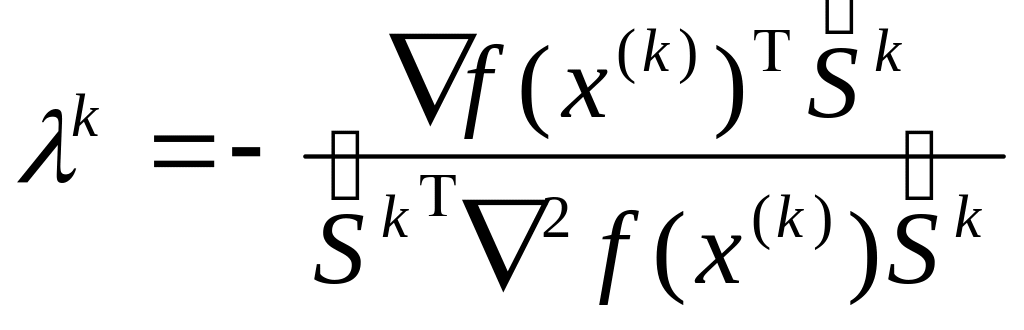Після визначення крапки повинне бути обране новий сполучений напрямок пошуку.

Метод сполученого градієнта Флетчера-Рівса.

У методі сполученого градієнта Флетчера-Рівса будується послідовність напрямків пошуку S, що є лінійними комбінаціями

1. - , поточного напрямку найшвидшого спуска;

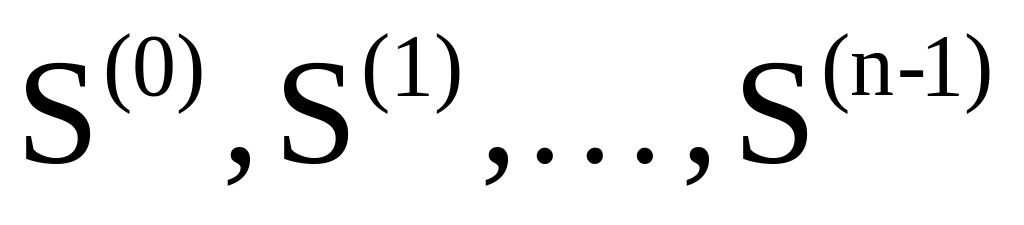2. , попередніх напрямків пошуку.

,

.

Вагові коефіцієнти вибираються таким чином, щоб напрямок був Н-Сполучений з усіма побудованими раніше напрямками пошуку. Тоді, з огляду на спряженість напрямків, виходить, що для обчислення нового напрямку пошуку в крапці використовуються значення тільки поточного й попереднього градієнтів. Всі вагові множники, що передують , а саме , виявляються нульовими. Загальна формула для напрямків пошуку виглядає в такий спосіб:

.

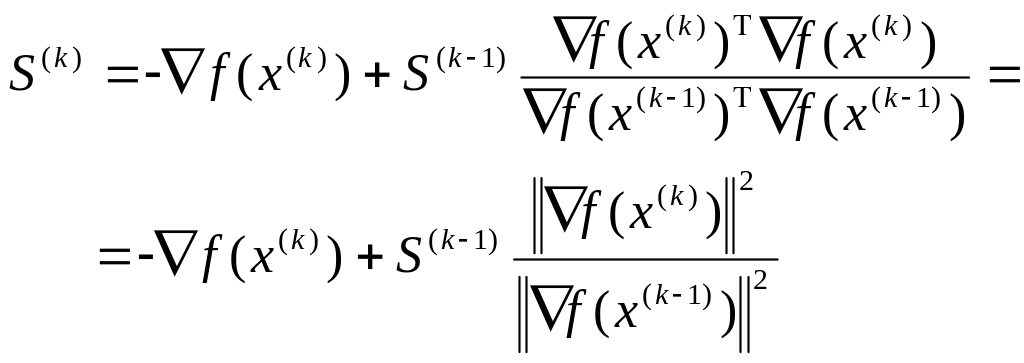Алгоритм методу сполученого градієнта Флетчера-Рівса.

Вихідні дані: початкова крапка ; параметр закінчення .

1. Обчислити в крапці

2. На k -му кроці за допомогою методів одномірного пошуку в напрямку перебуває мінімум цільової функції f(x) ( по ) - визначається довжина кроку .

3. Визначити крапку :

.

4. Обчислити значення 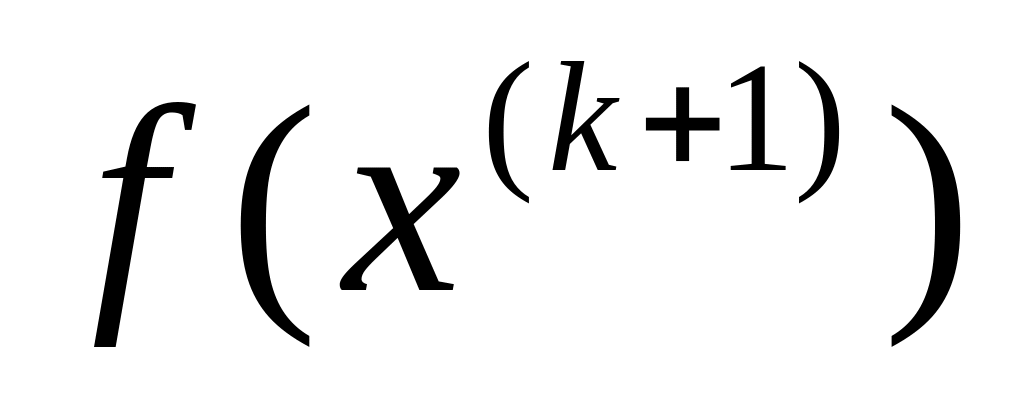й .

5. Обчислити напрямок :

.

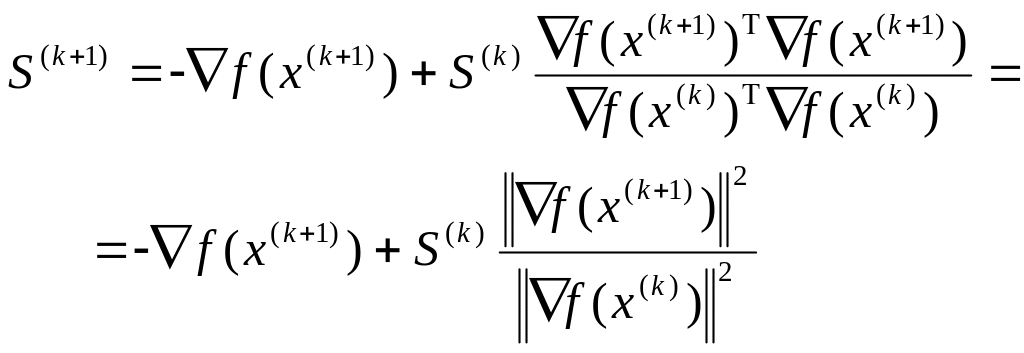6) Перевірити виконання нерівності

.

Якщо нерівність виконується, пошук кінчений, інакше, перейти до п.2.

Як критерій закінчення одномірного пошуку звичайно використовується умова:

Якщо f(x) - квадратична функція, для знаходження крапки мінімуму потрібно визначити ( n-1) напрямків, провести n пошуків уздовж прямій (при відсутності помилок округлення). Якщо f(x) - неквадратична функція, кількість напрямків і пошуків зростає.

Достоїнства:

1) Не потрібно оборотності матриці.

2) Невисокий рівень вимог до об'єму пам'яті ЕОМ дозволяє вирішувати задачі великої розмірності.

Недоліки:

Метод розроблений у припущенні про квадратичності цільової функції й відсутність помилок округлення при одномірному пошуку.

Порядок виконання роботи:

1. Ознайомитися з теоретичними відомостями, щодо методу який розглядається;

2. Вибрати варіант завдання, згідно списку студентів підгрупи у журналі;

3. Написати програму в середовище Delphi, яка реалізує данні методи;

4. За допомогою програми, виконати завдання, згідно варіанту;

5. Зробити висновки.

Варіанти завдань:

Методом сполучених напрямків знайти мінімум функції F(x), якщо пошук починається із точки х₀, =0,001.

1. F(x)=3x₁ - 2x₁x₂+4x₂ х₀=[1,2].

2. F(x)=2x₁² - 5x₁x₂+3x₂ х₀=[-2,1].

3.F(x)=3x₁² + x₂² - x₁x₂ x₀=[-2,1].

4. F(x)=2x₁² + 3x₁x ₂ -x₂² x₀=[-1,2].

5. F(x)=4x₁ - x₁x₂+3x₂ х₀=[-1,3].

6. F(x)=2x₁² - 2x₁x₂+x₂ x₀=[-2,-1].

7.F(x)=2x₁² +2 x₂² - 2x₁x₂ x₀=[2,2].

8. F(x)=2x12 + 4x1x 2 - 2x22 9.F(x)=4x1 - 2x1x2-3x2 10. F(x)=2x 12 + 2x1x2+2x2

х0=[-2,1]. x0=[-2,1]. x0-[-1,2].

Зміст звіту:

1. Титульний лист, згідно встановленого образка;

2. Основні теоретичні відомості;

3. Варіант завдання;

4. Код програми, яка реалізує даний метод;

5. Розв`язок з поясненнями;

6. Висновок.

Контрольні питання:

1. Яка система називається сполученою?

2. Як вибираються напрямки пошуку в даному методі?

3. Що таке матриця Гесе?

4. Як розкласти функціє у ряд Тейлора?

5. Опишіть алгоритм метода Флетчера-Рівса.

Лабораторна робота №12