
- •Міністерство освіти і науки України одеська державна академія холоду
- •Методи синтезу та оптимізації
- •Анотація
- •Іноді до системи обмежень (1.6) додають ще рівності
- •Тема: "Задача цілочисельного лінійного програмування. Метод гілок і кардонів"
- •Контрольні питання:
- •Лабораторна робота №9 Тема: " Метод найшвидшого спуску"
- •Лабораторна робота №10
- •(2 Години)
- •Лабораторна робота №11
- •(2 Години)
- •Тема: " Транспортна задача. Метод потенціалів"
- •Лабораторна робота №13 Тема: "Задача про призначення. Угорський метод"
- •Тема: "Задача опуклого квадратичного програмування. Квадратичний симплекс-метод"
- •Сєніна Тамара Іллівна, Іванова Олена Миколаївна методи синтезу та оптимізації
- •65082, Одеса, вул. Дворянська, 1/3
Контрольні питання:
1. Як формулюється задача цілочисельного лінійного программування?
2. Що таке нижня оцінку цільової функції ЦЗЛП?
3. У чому полягає суть методу Ленд-Дойга?
4. У чому відмінності при пошуку максимуму функції?
Лабораторна робота №6
Тема "Задачи дискретного програмування. Метод гілок і кордонів"
(2 години)
Ціль роботи: використовуючи метод гілок і кордонів вирішити задачу комівояжера, яка задана несиметричною матрицею.
Теоретичні відомості:
Комівояжер (агент, що рекламує товар своєї фірми) повинен відвідати n-1 інших міст і повернутися до вихідного пункту. Відомі відстані між містами dik, задані у вигляді таблиці. Потрібно встановити в, у якому порядку комівояжер повинен відвідувати міста, щоб загальна пройдена відстань була мінімальним.
Подання задачі комівояжера у вигляді графа.
Дуже наочно задачу комівояжера можна описати у вигляді графа G=(X, U), вершини якого відповідають містам, а дуги - дорогам, що з'єднують міста між собою. Кожній дузі, що з'єднує міста i, k, приписується число dik, яке називають довжиною дуги й рівне відстані між містами i і k. Якщо з кожного міста є безпосередній шлях у будь-яке інше місто без заходу в інші міста, то кожні дві вершини графа будуть з'єднані дугами в обох напрямках. Такий граф називають повним.
Елементарний шлях у графі, що проходить через всі вершини, називають гамільтоновим шляхом. Замкнутий елементарний шлях, тобто елементарний контур, називають гамільтоновим контуром. Таким чином, задача комівояжера зводиться до знаходження найкоротшого гамільтонова контуру. Основним видом задачі комівояжера вважається замкнутий варіант, коли задана вершина, у якій починається й закінчується маршрут комівояжера.
Якщо не зазначені ні початкова , ні кінцева вершини графа, то вводимо фіктивну вершину z, що з'єднується дугами нульової довжини з усіма вершинами графа в обох напрямках. Цю вершину приймаємо за початкову й знаходимо найкоротший гамільтонів контур. Виключивши з нього дугу нульової довжини, що виходить із z, одержимо найкоротший гамільтонів шлях.
Приведення до задачі цілочисельного лінійного програмування.
У графі G=(X, U), що відповідає задачі комівояжера, розглянемо деякий гамільтонів контур 1, i2,…,in,1... Сукупність дуг, що входять у гамільтонів контур, можна описати у вигляді матриці
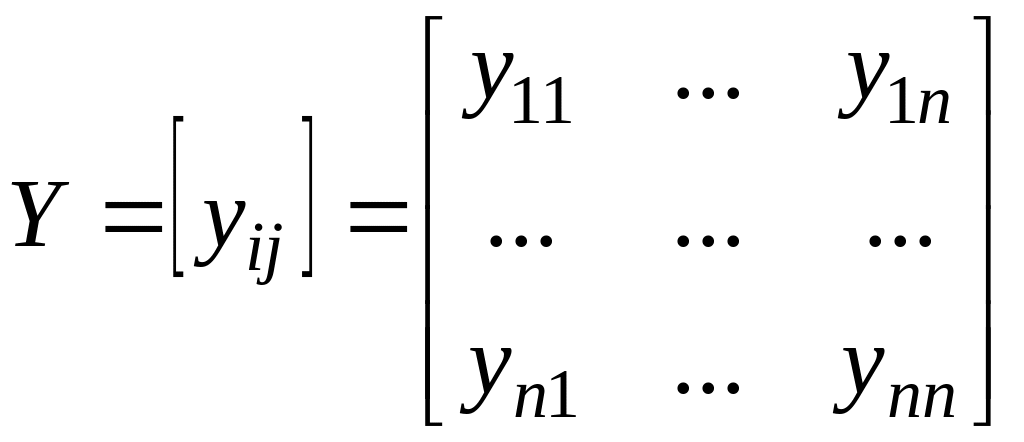 , (6.1)
, (6.1)
у якій
![]() (6.2)
(6.2)
Тому що кожна вершина зустрічається в гамільтоновому контурі один і тільки один раз, то в кожну вершину обов'язково входить одна й тільки одна дуга. Це означає, що в матриці(6.1) у кожному рядку й кожному стовпці повинна стояти одна й тільки одна одиниця, що математично запишеться у вигляді
![]() ;
;
![]() . (6.3)
. (6.3)
З обліком
(6.3) умова, щоб всі
![]() були рівні 0 або 1, можна замінити вимогою,
щоб всі
були позитивними цілими числами:
були рівні 0 або 1, можна замінити вимогою,
щоб всі
були позитивними цілими числами:
![]() ,
,
![]() ; (6.4)
; (6.4)
![]() , (6.5)
, (6.5)
де
![]() означає операцію узяття цілої частини
числа
.
означає операцію узяття цілої частини
числа
.
як бачимо, будь-який гамільтонів контур може бути описаний матрицею (6.1), елементи якої задовольняють співвідношенням (6.3)-(6.5). Довжина гамільтонова контуру дорівнює сумі довжин складових його дуг:
![]() . (6.6)
. (6.6)
Знаходження гамільтонова контуру мінімальної довжини зводиться до знаходження значень змінних , , що задовольняють лінійним рівнянням і нерівностям (6.3) і (6.4), умові цілочисельності (6.5) і обертаючих у мінімум лінійну форму (6.6), тобто до рішення задачі цілочисельного лінійного програмування.
Нехай
U - множина варіантів рішення деякої
задачі. Якщо ці варіанти перенумерувати
від 1 до m, то під U можна розуміти множина
номерів варіантів рішення, тобто
покласти![]() .
.
Позначимо через qi значення деякого параметра, що характеризує якість рішення в i-му варіанті. Оптимальне рішення буде таке, котре дає мінімальне значення
![]()
критерію
якості, що є точною нижньою границею
для множини![]() .
.
Введемо
поняття оцінки знизу для множини U, під
яким будемо розуміти таке значення
![]() , що задовольняє співвідношенню
, що задовольняє співвідношенню
![]() або
або
![]() . (6.7)
. (6.7)
Якщо в
співвідношенні (6.7) коштує знак нестрогої
нерівності, то оцінку
![]() будемо називати досяжною. метод гілок
і кордонів складається в послідовному
поліпшенні оцінки
й наближенні її до значення
будемо називати досяжною. метод гілок
і кордонів складається в послідовному
поліпшенні оцінки
й наближенні її до значення
![]() .
.
Припустимо, що маємо можливість одержати оцінку знизу як для всього множини U, та й для його різних підмножин.
Розіб'ємо
множину U не дві підмножини А и В з точними
нижніми границями критерію якості
![]() й
й
![]() ,
пов'язаними з
очевидним
співвідношенням
,
пов'язаними з
очевидним
співвідношенням
![]() .
.
Оскільки
в множинах А и В є присутнім менше число
елементів, чим у множині U, те є можливість
одержати оцінки
![]() ,
,
![]() ,
більше близькі до значень
,
,
чим у первісній множині U, що означає,
що оцінка
,
більше близькі до значень
,
,
чим у первісній множині U, що означає,
що оцінка
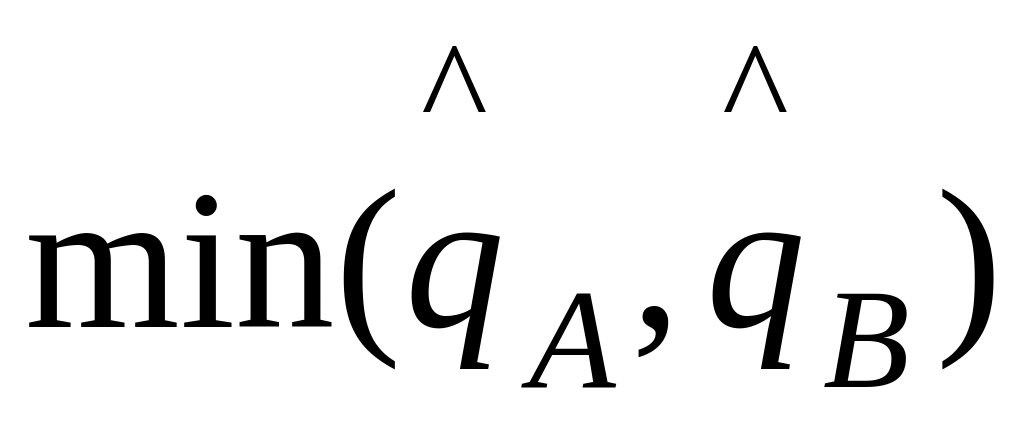 буде більш близька до
,
чим оцінка
.
буде більш близька до
,
чим оцінка
.
Є також
більша ймовірність того, що оптимальний
варіант, тобто варіант із найменшим
значенням
![]() ,
виявиться в тім з підмножин А и В, що має
найменшу оцінку знизу. Ця ймовірність
буде тим більше, чим більше відрізняються
друг від друга оцінки
й
,
тому розбивати множини U на підмножини
А и В бажано так, щоб оцінки знизу для
цих підмножин відрізнялися якнайбільше.
,
виявиться в тім з підмножин А и В, що має
найменшу оцінку знизу. Ця ймовірність
буде тим більше, чим більше відрізняються
друг від друга оцінки
й
,
тому розбивати множини U на підмножини
А и В бажано так, щоб оцінки знизу для
цих підмножин відрізнялися якнайбільше.
Якщо
виявилося, що
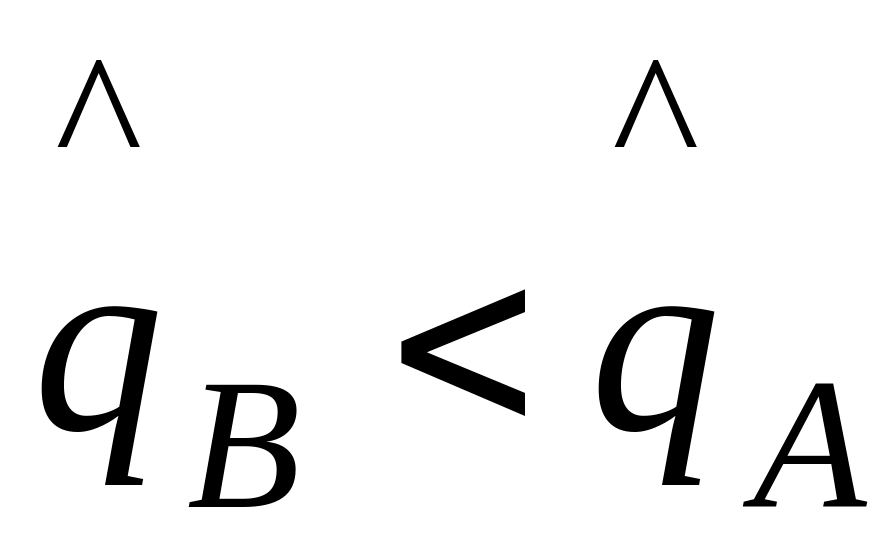 ,
тобто є підстави підозрювати, що
оптимальний варіант входить у множину
В то цю множину треба досліджувати більш
детальніше. Для цього розбиваємо його
у свою чергу на дві підмножини C і D так,
щоб оцінки
,
тобто є підстави підозрювати, що
оптимальний варіант входить у множину
В то цю множину треба досліджувати більш
детальніше. Для цього розбиваємо його
у свою чергу на дві підмножини C і D так,
щоб оцінки
![]() й
й
![]() розрізнялися якнайбільше. Якщо виявилося,
що
розрізнялися якнайбільше. Якщо виявилося,
що
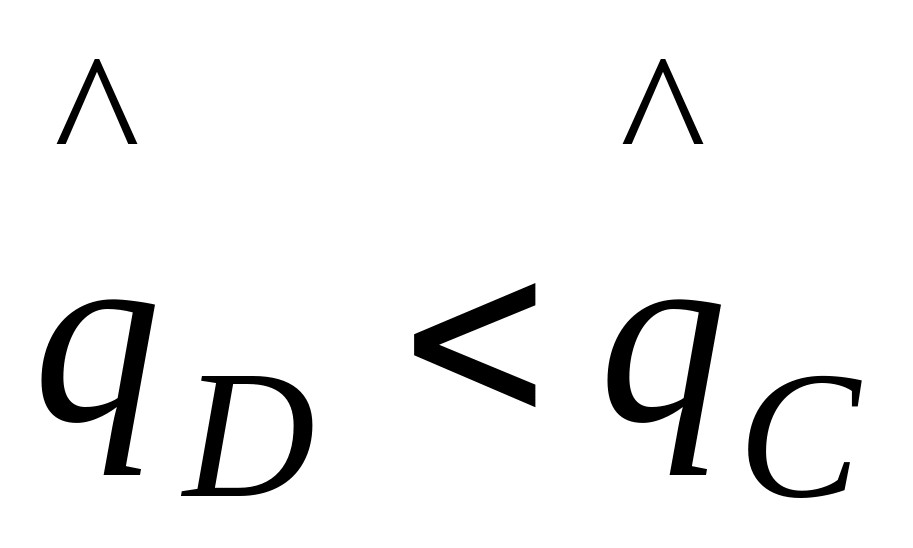 ,
то подібній же розбивці піддаємо множина
D і т.д. доти, поки не прийдемо до підмножини,
що складає всього з одного елемента зі
значенням параметра
,
то подібній же розбивці піддаємо множина
D і т.д. доти, поки не прийдемо до підмножини,
що складає всього з одного елемента зі
значенням параметра
![]() .
Всю процедуру розбивки зручно представити
у вигляді дерева розбивок.
.
Всю процедуру розбивки зручно представити
у вигляді дерева розбивок.
Однак
знайдений елемент зі значенням
може лише підозрюватися як оптимальний.
Необхідно перевірити, немає чи серед
нерозглянутих підмножин А, С й т.д.
елементу зі значенням
![]() .
При цьому множини, в яких
.
При цьому множини, в яких
![]() ,
можуть не розглядатися, оскільки елемента
з
у них бути не може.
,
можуть не розглядатися, оскільки елемента
з
у них бути не може.
Розбивка
вищевказаних множин або приведе до
елемента з
,
тоді цей елемент і повинен бути прийнятий
за оптимальний, або приведе до оцінок
знизу
.
У цьому випадку елемент зі значення
параметра
![]() й буде шуканим варіантом рішення задачі.
й буде шуканим варіантом рішення задачі.
Приклад виконання:
Вирішити задачу комівояжера методом гілок і границь, навести дерево розбивок. Задача комівояжера задана у вигляді матриці відстаней.
-
i
j
1
2
3
4
5
1
x
7
7
2
4
2
6
x
2
4
1
3
6
1
x
9
2
4
2
3
8
x
5
5
6
1
2
5
x
Рішення.
Для одержання оцінки знизу довжин множини всіх гамильтонових контурів скористаємося тим, що в кожний гамильтонів контур входить тільки по одному елементу з кожного рядка та з кожного стовпця матриці відстаней. Тому якщо елементи будь-якого рядка або будь-якого стовпця зменшити на яке-небудь число, то на це ж число зменшаться довжини всіх гамильтонових контурів. На цій властивості заснований метод приведення матриці відстаней.
Приведення
матриці може виконуватися по рядках та
стовпцям. Приведення матриці відстаней
по рядках полягає в тім, що з елементів
кожного рядка i
віднімають
найменший елемент цього рядка, позначуваний
hi.
При
цьому довжини всіх гамильтонових
контурів зменшаться на суму віднятих
з кожного рядка чисел, тобто на величину
![]() ,
залишаючись у той же час ненегативними.
,
залишаючись у той же час ненегативними.
-
i
j
1
2
3
4
5
1
x
5
5
0
2
2
2
5
x
1
3
0
1
3
5
0
x
8
1
1
4
0
1
6
x
3
2
5
5
0
1
4
x
1
Тому величина , рівна 7, дає деяку оцінку знизу довжин всіх гамильтонових контурів.
Отримана оцінка може бути поліпшена шляхом повторного приведення матриці відстаней по стовпцях. При цьому зі значень елементів кожного стовпця j наведених по рядках матриці відстаней віднімається найменший елемент цього стовпця, позначуваний gj.
-
i
j
1
2
3
4
5
1
x
5
4
0
2
2
5
x
0
3
0
3
5
0
x
8
1
4
0
1
5
x
3
5
5
0
0
4
x
0
0
1
0
0
Сума
віднятих при цьому чисел
![]() .
.
Уточнена оцінка знизу довжин гамильтонових контурів
![]()
Одержуємо наведену матрицю відстаней .
-
i
j
1
2
3
4
5
1
x
5
4
0
2
2
5
x
0
3
0
3
5
0
x
8
1
4
0
1
5
x
3
5
5
0
0
4
x
Метод приведення матриці відстаней будемо застосовувати й далі для одержання оцінок знизу різних підмножин множини гамильтонових контурів.
Розглянемо
тепер спосіб розбивки множини гамильтонових
контурів на підмножини. Візьмемо деяку
дугу (i, j). До першої підмножини віднесемо
всі гамильтонові контури, у які ця дуга
входить. Позначимо цю множину [(i, j)]. До
другої множини віднесемо всі гамильтонові
контури, у які дуга (i, j) не входить. Цю
множину позначимо
![]() .
.
Таблицю відстаней для множини [(i, j)] легко одержати, якщо врахувати, що включення дуги (i, j) у гамильтонів контур виключає можливість включення інших дуг, що знаходяться в i-рядку або j-м стовпці. Отже, таблиця відстаней для множини [(i, j)] виходить із первісної таблиці викреслюванням i-го рядка та j-го стовпця.
Для того щоб одержати таблицю відстаней для множини , треба в первісній таблиці заборонити рух по дузі (i, j), поклавши її довжину рівною нескінченності. Цю заборону руху по дузі (i, j) будемо позначати хрестом у відповідній клітині первісної таблиці.
В основу розбивки множини маршрутів на підмножини покладемо таку дугу, в якої в наведеній таблиці відстаней величина di,j=0. Але таких дуг може бути декілька. Вибираємо ту, для якої збільшення оцінки для множини буде найбільшим, тому що при цьому вийде найбільша різниця в оцінках для множин [(i, j)] і .
Позначимо
збільшення оцінки множини
через
![]() (i,
j). Значення цієї величини одержуємо
шляхом додавання найменших чисел в i-му
рядку та j-му стовпці.
(i,
j). Значення цієї величини одержуємо
шляхом додавання найменших чисел в i-му
рядку та j-му стовпці.
(1, 4)=2+3=5; (2, 3)=0+0=0; (2, 5)=0+1=1; (3, 2)=1+0=1;
(4, 1)=1+5=6; (5, 2)=0+0=0; (5, 3)=0+0=0
Найбільше збільшення оцінки для групи виходить для дуги (4, 1). Вилучив четвертий рядок та перший стовпець з наведеної матриці, отримуємо нову таблицю, що представляє собою таблицю відстаней для множини [(4, 1)].
-
i
j
2
3
4
5
1
5
4
х
2
2
x
0
3
0
3
0
x
8
1
5
0
0
4
x
При одержанні подібних матриць потрібно строго стежити за тим, щоб не могло вийти контурів, що не є гамильтоновими. Оскільки дуга [(4, 1)] уже введена в намічуваний гамильтонів контур, то потрібно накласти заборону на дугу [(1, 4)], позначивши клітинку [(1, 4)] хрестом, тому що дуга [(1, 4)] разом з дугою [(4, 1)] утворить контур.
Далі
аналогічно приводимо таблицю й обчислюємо
![]() для даної таблиці (
=2+3=5).
для даної таблиці (
=2+3=5).
-
i
j
2
3
4
5
1
3
2
х
0
2
x
0
0
0
3
0
x
5
1
5
0
0
1
x
Аналогічно обчислюємо (i, j):
(1, 5)=2; (2, 3)=0; (2, 4)=1; (2, 5)=0; (3, 2)=1;
(5, 2)=0; (5, 3)=0
Найбільше збільшення оцінки для групи виходить для дуги [(1, 5)], що також уводимо в намічуваний гамильтонів контур, одержуючи ланцюжок [(4, 1, 5)]. Вилучив перший рядок й п'ятий стовпець з матриці, приходимо до нової таблиці для множини [(4, 1) (1, 5)], у якій необхідно накласти заборону на дугу [(5, 4)], що утворить контур з ділянкою [(4, 1, 5)].
-
i
j
2
3
4
2
x
0
0
3
0
x
5
5
0
0
х
Отримана таблиця є наведеною. Тому для неї відразу ж знаходимо значення (i, j):
(2, 3)=0; (2, 4)=5; (3, 2)=5; (5, 2)=0; (5, 3)=0
Як бачимо, найбільші значення (i, j) вийшли рівними для дуг (2, 4) і (3, 2). Тому обидві ці дуги можна віднести до намічуваного гамильтонового контуру, одержуючи, таким чином, послідовність дуг [(3, 2)], [(2, 4)], [(4, 1)], [(1, 5)], для замикання якої не вистачає лише дуги [(5, 3)]. Додаючи цю дугу, одержуємо передбачуваний оптимальний гамильтонів контур [(3, 2, 4, 1, 5, 3)] довжиною 13 (L=8+5+0+0=13).
Аналізуючи нерозглянуті раніше підмножини [(4, 1)], [(4, 1), (1.5)], [(4, 1), (1, 5), (2, 4)], переконуємося, що їхньої оцінки знизу більше, ніж 13, так що ці підмножини не можуть містити гамильтонові контури коротші знайденого. Отже, подальша перевірка не потрібна й отриманий гамильтонів контур є оптимальним.
Б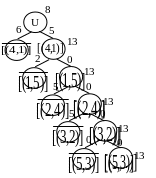 удуємо
дерево розбивок.
удуємо
дерево розбивок.
Порядок виконання роботи:
Ознайомитися з теоретичними відомостями, щодо методу який рзглядається;
Вибрати варіант завдання;
Скласти алгоритм методу гілок і кордонів для вирішення задачі комівояжера;
Написати програму в середовище Delphi, яка реалізує даний метод;
За допомогою програми, виконати завдання, згідно варіанту;
Побудувати дерево розбивок;
Написати висновки.
Варіанти завдань:
Розв`язати
задачу комівояжера з несиметричною
матрицею
![]() (n=6) методом гілок і кордонів.
(n=6) методом гілок і кордонів.
-
1
∞
31
15
19
8
55
19
∞
22
31
7
35
25
43
∞
53
57
16
5
50
49
∞
39
9
24
24
33
5
∞
14
34
26
6
3
36
∞
2
∞
19
25
11
2
35
37
∞
26
58
21
43
10
50
∞
39
22
3
38
39
24
∞
38
45
27
9
32
9
∞
2
33
48
60
53
1
∞
3
∞
16
13
35
41
52
19
∞
29
31
26
18
57
51
∞
44
51
7
5
40
32
∞
14
16
33
41
28
3
∞
53
19
54
24
10
41
∞
4
∞
39
45
2
51
33
30
∞
20
33
40
35
54
16
∞
55
22
56
19
36
25
∞
18
43
29
8
8
12
∞
25
16
47
31
14
8
∞
5
∞
21
40
28
60
52
58
∞
11
39
22
56
22
12
∞
23
14
19
25
47
51
∞
20
54
47
43
18
42
∞
52
44
49
50
52
29
∞
6
∞
6
56
35
48
29
34
∞
46
46
55
26
29
31
∞
32
13
42
26
34
12
∞
17
7
38
35
40
13
∞
47
60
25
59
36
31
∞
7
∞
22
26
56
38
60
34
∞
12
51
37
27
45
33
∞
44
47
37
39
7
16
∞
57
8
35
56
40
58
∞
27
9
20
36
31
18
∞
8
∞
4
39
22
10
47
58
∞
56
18
4
35
34
29
∞
17
57
18
52
4
22
∞
15
37
41
44
25
11
∞
32
11
6
19
2
58
∞
9
∞
14
40
33
16
51
48
∞
34
4
11
24
57
35
∞
24
38
52
30
50
44
∞
9
31
18
42
24
31
∞
30
1
38
31
19
32
∞
10
∞
56
48
39
3
40
47
∞
50
4
10
49
48
50
∞
42
19
16
24
44
47
∞
23
33
38
17
6
51
∞
26
29
59
55
34
18
∞
Зміст звіту:
Титульний лист, згідно встановленого образца;
Основні теоретичні відомості;
Варіант завдання;
Блок-схема;
Код програми з коментаріями;
Розв`язок з поясненнями;
Висновок.
Контрольні питання:
Що таке гамільтонів контур?
Яка задача має назву незамкнута задача комівояжера?
Як звести задачу комівояжера до задачи цілочисельного лінійного програмування?
Як представити задачу комівояжера у вигляді графа?
Що таке дерево розбивок?
Алгоритм методу гілок і кордонів.
Лабораторна робота №7
Тема: "Методи одновимірної оптимізації. Метод золотого перерізу. Метод дихотомії. Метод Фiбоначчi."
(2 години)
Ціль роботи: ознайомитися з методами одновимірної оптимізації. За допомогою методів: золотого перерізу, дихотомії та Фібоначі вирішити задачу оптимізації функції, порівняти отримані результати.
Теоретичні відомості.
Метод золотого перерізу.
Метод золотого перерізу (МЗП) застосовується для пошуку мінімуму унiмодальної функції однієї змінної y=F(x), що задана на проміжку [A,B]. Алгоритм методу реалізується у вигляді послідовності кроків, на кожному з яких здійснюється звуження інтервалу, що містить точку мінімуму.
На початку обчислень покладають A{0} = A, B{0} = B.
На s-у кроцi визначають величини
L{s} = B{s} G(B{s} A{s}),
R{s} = A{s} + G(B{s} A{s}),
де стала G = (Ö5 1)/2 » 0.618. Покладають
A{s+1} = A{s}, B{s+1} = R{s}, якщо F(L{s}) £ F(R{s}),
A{s+1} = L{s}, B{s+1} = B{s}, якщо F(L{s}) > F(R{s}).
Iтерацiї продовжують доти, поки не буде виконуватись нерівність
B{s} A{s} £ e,
де e > 0 задане число, яке визначає похибку розв'язку задачі.
На кожному кроцi МЗП, починаючи з 1-го, обчислюється лише одне значення функції F(x), тому що одна з точок золотого перерізу на попередньому кроцi здійснює золотий переріз проміжку на наступному кроцi.
За наближений розв'язок задачі приймають
x* = (A{s} + B{s})/2, y* = F(x*).
Метод дихотомії.
Метод дихотомії (МД) застосовується для пошуку мінімуму унiмодальної функції однієї змінної y=F(x), що задана на проміжку [A,B].
Алгоритм методу реалізується у вигляді послідовності кроків, на кожному з яких здійснюється звуження інтервалу, що містить точку мінімуму.
На початку обчислень покладають A{0} = A, B{0} = B.
На s-у кроцi визначають величини
L{s} = (A{s} + B{s} D)/2,
R{s} = (A{s} + B{s} + D)/2,
де D > 0 достатньо мале число. Покладають
A{s+1} = A{s}, B{s+1} = R{s}, якщо F(L{s}) £ F(R{s}),
A{s+1} = L{s}, B{s+1} = B{s}, якщо F(L{s}) > F(R{s}).
Iтерацiї продовжують доти, поки не буде виконуватись нерівність
B{s} A{s} £ e,
де e>0 задане число, яке визначає похибку розв'язку задачі.
За наближений розв'язок задачі приймають
x* = (A{s} + B{s})/2, y* = F(x*).
Метод Фiбоначчi
Метод Фiбоначчi (МФ) застосовується для пошуку мінімуму унiмодальної функції однієї змінної y=F(x), що задана на проміжку [A,B].
Алгоритм методу реалізується у вигляді послідовності кроків, на кожному з яких здійснюється звуження інтервалу, що містить точку мінімуму.
На початку обчислень покладають A{0} = A, B{0} = B.
На s-у кроцi визначають величини
L{s} = B{s} G{s} (B{s} A{s}),
R{s} = A{s} + G{s} (B{s} A{s}),
де G{s}=Fi(Ns1)/Fi(Ns), s=0,...,N3, G{N2}=(1+e)/2 або
(1e)/2, N задане число iтерацiй, e>0, Fi(j) числа Фiбоначчi, що задаються рекурентним співвідношенням
Fi(j) = Fi(j1) + Fi(j2), j ³ 2, Fi(0) = Fi(1) = 1.
Покладають
A{s+1} = A{s}, B{s+1} = R{s}, якщо F(L{s}) £ F(R{s}),
A{s+1} = L{s}, B{s+1} = B{s}, якщо F(L{s}) > F(R{s}).
За наближений розв'язок задачі приймають
x* = (A{N} + B{N})/2, y* = F(x*).
Для МФ у випадку заздалегідь фіксованого числа iтерацiй довжина кінцевого інтервалу пошуку мінімальна.
При розв'язуванні задачі максимiзацiї функції F(x) необхідно замінити її на функцію F(x).
Порядок виконання роботи:
Ознайомитися з методами одновимірної оптимізації;
Вибрати варіант завдання, згідно списку студентів півгруппи у журналі;
Написати програму в середовище Delphi. Программа повинна складатися з 3 підпрограм: метод золотого перетину, метод дихотомії, метод Фібоначі;
За допомогою програми, виконати завдання, згідно варіанту;
Визначити швидкість збігу кожного метода;
Порівняти відповіді, отримані різними методами
Написати висновки до роботи.
Варіанти завдань:
Знайти методами золотого перерізу, Фібоначі та дихотомії найменше значення наступних функцій на вказаних проміжкахe=0,5:
1) F(x) = |||x21|1|1|, x Î [2, 2];
2) F(x)
= 2x33x212x+1+![]() , x
Î
[2,
2];
, x
Î
[2,
2];
3) F(x) = (x+1)2 ln(x+1)+x exp(x), x Î [0, e];
4) F(x) = sin(x) sin(2x) + arccos(x2), x Î [0.75, 0.75];
5) F(x) = arctg(x) ln(x)/2, x Î [0.65, 1.75];
6) F(x)
= x+
![]() +
exp(x)
x2, x
Î
[0,
4];
+
exp(x)
x2, x
Î
[0,
4];
7) F(x) = 4 x/(x2 + 4)[x2 (x 2)](2/5), x Î [2, 2];
8) F(x) = 2x3-2x, x Î [1, 2];
9) F(x) = -x3+3(1+x)(ln(x+1)-1), x Î [1.5, 2];
10)F(x) = (x+2)2 lg(x+1)-xx, x Î [-2,5].
Зміст звіту:
Титульний лист, згідно встановленого образца;
Основні теоретичні відомості;
Варіант завдання;
Код програми, яка реалізує даний метод;
Розв`язок з поясненнями;
Висновок.
Контрольні питання:
Які функції називають унімодальними?
Що таке випукла функція?
Який алгоритм метод Золотого перерізу?
Наведіть перші 10 чисел Фібоначі.
Як реалізується метод Фібоначі?
Чому дорівнює число золотого перізу? З яких міркувань воно було отримане?
Як розрахувати швидкість збігу для кожного з методів?
Лабораторна робота №8
Тема: "Одномірна оптимізація. Квадратична інтерполяція"
(2 години)
Ціль роботи: на практиці застосувати метод квадратичної інтерполяції для знаходження екстремуму функції однієї змінної.
Теоретичні відомості.
Ідея методу квадратичної інтерполяції, який називають методом Пауела, полягає в побудові інтерполяційного багаточлена 2-го ступеня по трьох крапках, узятим поблизу мінімуму. Положення мінімуму багаточлена приймається як нове наближення до шуканої крапки мінімуму функції.
Нехай f1, f2, f3 - значення функції f(x) у крапках x1, x2 і x3, відповідно. Запишемо інтерполяційний багаточлен у формі Лагранжа:
 .
(8.1)
.
(8.1)
Диференціюючи цей вираз, отримаємо першу похідну:
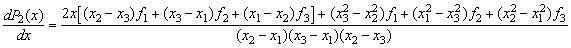 .
(8.2)
.
(8.2)
Дорівнюючи похідну нулю, знайдемо положення мінімуму P2(x):
 .
(8.3)
.
(8.3)
Позначимо через x4 наближення до крапки мінімуму, розраховане по формулі (8.3). Відкинемо одну з колишніх крапок так, щоб три крапки, що залишилися (включаючи нову) обмежували мінімум. Повторюючи крок, знайдемо нове наближення за допомогою квадратичної інтерполяції, залишимо три найближчі до мінімуму крапки й т.д. Процес закінчують, коли довжина інтервалу невизначеності або відносне зниження значення функції на двох послідовних кроках стають менше заданої величини.
У міру наближення до мінімуму величини x1, x2 і x3, що входять у формулу (8.3), усе більше зближаються (як і відповідні значення функції). При цьому безпосереднє використання (8.3) може привести до обчислювальних труднощів через втрату точності в результаті вирахування близьких величин. Тому формулу приводять до більше зручного для обчислень виду:
![]() (8.4)
(8.4)
Перший доданок в (8.4) визначає середину відрізка [x1, x2] і не страждає від втрати точності при зближенні крапок. Другий доданок мало в порівнянні з першим (чисельник дробу містить добуток трьох малих різниць, тоді як знаменник являє собою комбінацію перших ступенів цих різниць). Звичайно, другий доданок буде знайдено зі збільшеною відносною погрішністю, через втрату точності, але ця погрішність мала і її вплив на кінцевий результат незначний.
Метод Пауела в достатній близькості від мінімуму має квадратичну збіжність, і в цьому його перевага в порівнянні з лінійно збіжним методом золотого перерізу. Однак, якщо початковий інтервал невизначеності великий, апроксимація функції за допомогою багаточлена другого ступеня може виявитися занадто грубої, що приведе до вповільнення збіжності. Тому на практиці найчастіше користуються комбінованим методом, що одержав назву методу Брента. На першому етапі положення мінімуму уточнюють за допомогою методу золотого перерізу, що гарантує постійну швидкість скорочення інтервалу невизначеності, а коли цей інтервал стане досить малим, переходять до квадратичної інтерполяції по формулі (8.4), що швидко приводить до кінцевого результату.
Порядок виконання роботи:
Ознайомитися з теоретичними відомостями, щодо методу який розглядається;
Вибрати варіант завдання, згідно списку підгрупи у журналі;
Написати блок-схему реалізації метода квадратичної інтерполяції;
Написати програму в середовище Delphi, яка реалізує даний метод;
За допомогою програми, виконати завдання, згідно варіанту;
Зробити висновок.
Варіанти завдань:
Методом Пауела знайти мінімум функції F(x), починаючи пошук з т. х0.
1. F(x)=x2 - 4x, х0=2.
2. F(x)=x2 - x+2, х0=1.
3. F(x)=x2 –4x+1, х0=1.
4. F(x)=2x2 - x, х0=0.
5. F(x)=x2 - x+4, х0=1,5.
6. F(x)=3x2 -2 x-2, х0=2.
7. F(x)=x2 - 3x+1, х0=1.
8. F(x)=1,5x2 - x+2, х0=1.
9. F(x)=x2 – 1,1x, х0=1,5.
10. F(x)=2x2 – 1,5x+2, х0=2.
Зміст звіту:
Титульний лист, згідно встановленого образка;
Основні теоретичні відомості;
Варіант завдання;
Блок-схема;
Код програми, яка реалізує даний метод, з поясненнями;
Відповідь;
Висновок.
Контрольні питання:
У чому полягає метод квадратичної інтерполяції?
Запишіть інтерполяційний багаточлен у формі Лагранжа.
Які відмінності має метод Брента від метода Пауела?
Графічно проілюструйте метод квадратичної інтерполяції.
