1. Основные характеристики случайных процессов: математическое ожидание, корреляционная функция, дисперсия. Типовые задачи с решениями

1. Найти математическое ожидание, корреляционную функцию и дисперсию случайного процесса

X(t) = Ysin2t + Zcost,

где Y и Z – случайные величины, характеризуемые следующими числовыми характеристиками: m_Y= 2, m_Z = 1, D_Y = 0.1, D_Z = 0.05,

корреляционный момент между случайными величинами Y и Z

K_YZ = 0.

Решение

В рассматриваемом случайном процессе множители sin2t и cost не являются случайными величинами. Поэтому при определении математического ожидания процесса Х(t) они выносятся за знак математического ожидания случайных величин Y и Z. Математическое же ожидание суммы равно сумме математических ожиданий составляющих случайного процесса:

M[X(t)] = = sin2tM[Y]+ costM[Z].

Подставляя в последнее выражение числовые значения M[Y] и M[Z], получим

2sin2t + cost.

Поскольку случайные величины Y и Z некоррелированы, корреляционная функция процесса X(t) равна сумме корреляционных функций его составляющих. При этом коэффициенты (неслучайные процессы) выносятся за знак корреляционных функций случайных величин Y и Z в виде произведения неслучайных процессов в двух сечениях по времени t₁ и t₂. Учитывая также, что

К_YY(t₁, t₂)=D_Y и K_ZZ(t₁, t₂)=D_Z, будем иметь

K_XX(t₁, t₂)=sin2t₁sin2t₂D_Y + cost₁cost₂D_Z.

Подставляя числовые значения для D_Y и D_Z, получим

K_XX(t₁, t₂)=0.1sin2t₁sin2t₂ + 0.05cost₁cost₂.

Дисперсия случайного процесса X(t) определится как D_X(t)=K_XX(t₁, t₂) при t₁=t₂=t:

D_X(t) = 0.1sin²2t + 0.05cos²t.

2. Найти математическое ожидание, корреляционную функцию и дисперсию процесса

Х(t) = sintY(t) + cost,

где Y(t) – случайный процесс, характеризуемый M[Y(t)] и K_YY(t₁, t₂),

cost – неслучайный процесс.

Решение

Математическое ожидание процесса X(t) определится как:

sint + cost.

Корреляционная функция процесса X(t) запишется в виде

K_XX(t) = sint₁sint₂K_YY(t₁, t₂),

( корреляционная функция неслучайного процесса равна нулю).

Соответственно дисперсия случайного процесса X(t) будет

D_X(t) = sin²t(t).

2. Линейное преобразование случайных процессов при использовании понятия спектральной плотности

ТИПОВАЯ ЗАДАЧА С РЕШЕНИЕМ

Используя понятие спектральной плотности, найти дисперсию процесса на выходе линейной системы (рис.2.1) при воздействии на её входе стационарного процесса X(t), характеризуемого корреляционной функцией () = e^{}.

Рис. 2.1

Решение

Задача может быть решена как с помощью интегрального преобразования Фурье, т.е. с использованием понятий спектральной плотности стационарного процесса S_XX() и передаточной функции линейной системы H(j), так и с помощью двустороннего преобразования Лапласа, т.е. с применением S_XX(p) и Н(p).

Спектральная плотность стационарного эргодического случайного процесса X(t) связана с корреляционной функцией этого процесса с помощью соотношений Винера-Хопфа, полученных на основе двойного интеграла Фурье:

S_XX() =

При использовании двустороннего интегрального преобразования Лапласа приведенные соотношения принимают вид:

S_XX(p) = (2.1)

(2.2)

Корреляционная функция K_XX() при использовании последнего выражения может быть определена с помощью теории вычетов:

K_XX() = при  (2.3)

K_XX() = при , (2.4)

где

_к и _к - левые и правые полюса S_XX(p), соответственно.

Дисперсия процесса X(t) определяется по выражениям (2.2)…(2.4) при =0 : D_X=K_XX(0).

В рассматриваемом примере

S_XX() = D_X + D_X = (2.5)

S_XX(p) = D_X + D_X (2.6)

Следует отметить, что выражение (2.5) может быть получено из выражения (2.6), если в последнем положить p=j.

Передаточную функцию схемы рис.2.1 получим, используя одностороннее интегральное преобразование Лапласа и полагая, что случайный процесс X(t) представляет собой напряжение на входе схемы. Тогда

H(p)=Y(p)/X(p)=I(p) R₂, (2.7)

где I(p)=X(p)/(R₂+R₁+pL) – операторное изображение тока. (2.8)

Подставляя (2.8) в (2.7), получим

H(p)=R₂/(R₁+pL)=₂/(p+) , (2.9)

где ₂=R₂/L , =(R₁+R₂)/L – декремент контура (=1/T, T – постоянная времени контура.

Спектральная плотность случайного процесса на выходе схемы определится как

S_YY(p)=S_XX(p)H(p)H(-p) = (2.10)

или

S_YY()=S_XX()H(j)H(-j) = (2.11)

Для определения корреляционной функции случайного процесса Y(t) воспользуемся выражениями (2.3),(2.4) и (2.10). Спектральная плотность S_YY(p) имеет два левых полюса p₁=- и p₂=- и два правых полюса p₁= и p₂=. Беря с помощью второй теоремы разложения Хевисайда оригиналы изображений (2.3) и (2.4) , получим

K_YY() = при , (2.12)

K_YY() = при   0. (2.13)

Объединяя выражения (2.12) и (2.13), получим:

K_YY() = при . (2.14)

Дисперсия стационарного процесса на выходе схемы рис.1 определится как

D_Y = K_YY(0) = D_X (2.15)

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ПО РАЗДЕЛАМ 1 И 2

Задания 1 и 2

Задача 1. Во всех вариантах найти математическое ожидание, корреляционную функцию и дисперсию случайного процесса X(t) при заданных числовых характеристиках составляющих этого процесса.

Номер варианта	X(t)	Числовые характеристики составляющих X(t)
1	Ycost + Zsint + 5t	M[Y]=1; M[Z]=0.2; D[Y]=0.1; D[Z] = 0.004; KYZ= 0
2	Ysint	M[Y] = 1; D[Y] = 0.2
3	Yt – Zt2	M[Y] = 3; M[Z] = 0.5; D[Y]=1; D[Z] = 0.5; KYZ= 0
4	2Ysint + 3Zt2 + 5	M[Y]= 1; M[Z] = 2; D[Y]= 0.1; D[Z] = 0.05; KYZ = 0
5	t–3cost+Y(t + cost)+Zcos2t	M[Y]=M[Z]=0; D[Y] = 1; D[Z] = 2; KYZ = 0
6	costY(t) + sint	KYY(t1, t2)
7	Y(t) + tcost	KYY(t1, t2)
8	Y	M[Y] = 2; D[Y] = 0.01
9	Ycost + 5	M[Y] = 0; D[Y] = 1
10	Ye-t + sint	M[Y] = D[Y] = 1
11	Ye-t + Zet	M[Y]= 2; M[Z]=-2; D[Y] = D[Z] = 1; KYZ= 0
12	Ysint + 4e-t	M[Y] = 2; D[Y] = 0.1
13	Yt + Ze-t + Vsint	M[Y]=M[Z]=M[V]=D[Y]=D[Z]=D[V]=1; KYZ=KYV=KZV= 0
14	Ysint + Zcost + Ve-t	M[Y]=2; M[Z]=M[V]=1; D[Y]=D[V]=0.1; D[Z]=0.05; KYZ=KYV=KZV=0
15	Yte-t + Z	M[Y]=2; M[Z]=1; D[Y]=0.2; D[Z]=0.1; KYZ= 0
16	5Ye-t + sint	M[Y]=2; D[Y]=4
17	Ye-t + Zsint	M[Y]=D[Y]=1; M[Z]=2; D[Z]=1; KYZ= 0
18	Ye-t + Zcost + 3sint	M[Y]=M[Z]=2; D[Y]=2; D[Z]=1; KYZ= 0

Задача 2. Используя понятие спектральной плотности, найти корреляционную функцию и дисперсию стационарного случайного процесса на выходе линейной системы при известной корреляционной функции стационарного эргодического процесса на её входе: K_XX() = D_Xe^{}

Варианты линейных систем

№ 1 № 2

№ 3 № 4

№ 5 № 6

№ 7 № 8

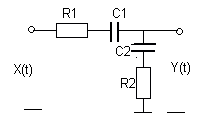№ 9 № 10

№ 11 № 12

№ 13 № 14

№ 15 № 16

№ 17 № 18