13.2. Транспортная сеть. Расчет кратчайших расстояний
Необходимость определения кратчайших расстояний возникает всегда, если требуется получить оптимальный вариант организации перевозок. При густоразветвленной сети автомобильных дорог, когда между пунктами отправления и пунктами назначения имеется несколько вариантов сообщений, определить кратчайший путь бывает сложно. Для нахождения оптимального варианта сообщения применяют математические методы, основанные на использовании в качестве исходной информации транспортной сети, отражающей транспортные связи между пунктами отправления и назначения грузов (пассажиров).
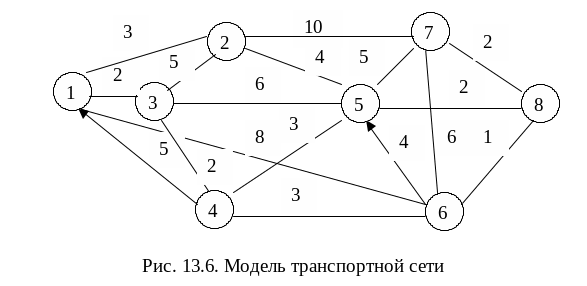
Транспортная сеть учитывает только ту часть дорожной сети, по которой возможно организовать соответствующие перевозки, то есть учитываются ограничения по состоянию улиц (дорог), одностороннее движение, ограничения на движение грузового транспорта, на полную массу транспортного средства, нагрузка на ось и другие. Модель транспортной сети представляют в виде графа (рис. 13.6).
Граф состоит из вершин, условно обозначающих пункты отправления, назначения, пересечения дорог, размещения АТП и другие, и отрезков дорог (их называют ребрами), соединяющих вершины. По некоторым из ребер движение может быть разрешено только в одну сторону (ребра 4–1, 6–5 на рис. 13.6), такие ребра называют дугами. Всякое неориентированное ребро может быть представлено как две равноценные, но противоположно направленные дуги.
Транспортная сеть может быть представлена только связным графом, таким, в котором каждая вершина может быть соединена с любой другой его вершиной. Для выполнения этого условия каждая вершина графа должна иметь как минимум одну входящую и одну выходящую дугу.
Моделирование транспортной сети начинают с размещения вершин. Вершины присваивают грузообразующим и грузопоглощающим пунктам, центрам крупных жилых кварталов, обособленных населенных пунктов, пересечениям улиц и дорог. Вершины, имеющие между собой транспортное сообщение, связывают ребрами или (в случае односторонней связи) ориентированными дугами.
Задача о кратчайшем пути может быть сформулирована следующим образом: для связного графа, имеющего R вершин и N ориентированных дуг длиной C ij , требуется найти кратчайшие расстояния от заданной вершины i0 до всех остальных вершин этого графа. В каждую вершину графа может входить только одна дуга, принадлежащая какому-либо кратчайшему пути.
Все алгоритмы решения такой задачи предусматривают последовательное определение расстояний до смежных с заданной вершиной и выбор из них минимальных. Задачи могут решаться как вручную, так и с использованием ЭВМ.
Для решения задачи все множество вершин сети разбивают на три группы:
1 – вершины, расстояния до которых уже найдены;
2 – вершины, смежные (связанные дугой) с вершинами первой группы;
3 – все остальные вершины.
Среди вершин второй группы выбирается вершина с наименьшим расстоянием до вершины первой группы и такая вершина переводится из второй группы в первую. После этого вновь определяется состав вершин второй группы с учетом перевода одной из них в первую группу и процесс повторяется. Расчет выполняется до тех пор, пока все вершины из третьей группы не будут переведены последовательно во вторую и затем в первую группу.
Один из методов решения задачи приведен в качестве примера [15, с. 16–24].
Пусть необходимо определить кратчайшие расстояния от вершины 1 до всех остальных, показанных на рис. 13.6. Из схемы следует, что известно расстояние до вершины 1 (оно равно нулю) и от первой вершины до смежных с ней вершин (2, 3 и 6). Вершина 4 также имеет связь с вершиной 1, но эта связь односторонняя, поэтому от вершины 1 с вершиной 4 связи нет.
Распределение вершин по группам с указанием номеров предшествующих вершин и расстояний от начальной вершины показывают в виде таблицы (табл. 13.1).
Вершина 1 начальная, расстояние до нее равно нулю, ее считают в первой группе; вершинам 2, 3 и 6 предшествует вершина 1, расстояния до них соответственно 3, 2 и 8 км, их можно отнести ко второй группе; расстояния до остальных вершин пока не определены, следовательно, они относятся к третьей группе. На этом этапе расстояния до них считают равными какому-то большому числу и обозначают буквой М, предшествующей вершины для них пока также нет, проставляем 0.
Из расстояний до вершин второй группы наименьшее – до вершины 3, эту вершину из второй группы можно перевести в первую, кратчайшее расстояние до нее r3 = 2.
На следующем этапе определяют вершины, смежные с вершиной 3: это вершины 1, 2, 4, 5. Вершина 1 входит в первую группу, ее во внимание не принимают. Расстояния до остальных вершин определяют по формуле
d j = r i + l ij, (13.6)
где d j – расстояние от начальной точки до j-й вершины;
r i – кратчайшее расстояние от начальной точки до предше-
ствующей i-й вершины;
l ij – длина ребра (дуги), связывающего i-ю и j-ю вершины.
d2 = r3 + l 3,2 = 2 + 5 = 7,
d4 = r3 + l 3,4 = 2 + 2 = 4,
d5 = r3 + l 3,5 = 2 + 6 = 8.
Вершина 2 уже во второй группе, расстояние до нее больше, чем записано в табл. 13.1, поэтому оставляют его прежнее значение (3 км). Вершины 4 и 5 переводят во вторую группу, предшествующей для них становится вершина 3. Результаты расчета заносят в табл. 13.2.
Из вершин второй группы (2, 4, 5, 6) кратчайшее расстояние до вершины 2; ее переводят в первую группу, расстояние до нее r2 = 3.
Далее начинается следующий этап по определению вершин, смежных с вершиной 2, и расстояний до них. Результаты последующих расчетов приведены в табл. 13.3 – 13.6.
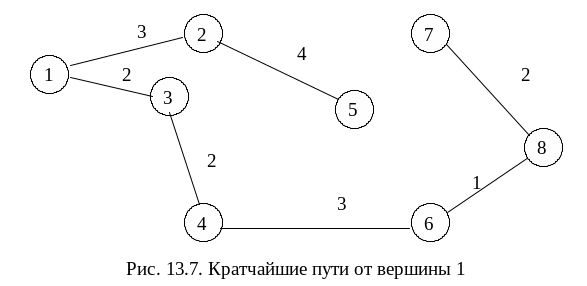
В последней таблице (табл. 13.6) указаны кратчайшие расстояния от всех вершин до вершины 1 и номера предшествующих вершин. По данным этой таблицы можно определить кратчайший маршрут, перебирая последовательно предшествующие вершины. Из всех вершин наиболее удалена от начальной вершина 7, ей предшествует вершина 8, затем вершины 6, 4, 3, 1. Таким образом, кратчайший путь от вершины 1 к вершине 7 проходит через вершины 3, 4, 6, 8. Кратчайшие маршруты показаны на рис. 13.7.
На практике, после приобретения соответствующих навыков, пользуются более простым способом, используя для расчетов одну таблицу (табл. 13.10). Расчет выполняют аналогично рассмотренному [3, с. 122–126].
В табл. 13.7 показан первый шаг расчета: смежные с вершиной 1 вершины 2, 3, 6, потенциалы их соответственно П2 = 3, П3 = 2, П6 = 8.
Минимальное значение потенциала у вершины 3 (выделен курсивом П3 = 2); вершину 3 переводим в первую группу, смежные с ней вершины – 2, 5, 4; определяем их потенциалы и сравниваем с уже определенными ранее.
Потенциал вершины 2 П2 = 7; ранее его определили (П2 = 3), следовательно, значение потенциала П2 = 7 во внимание не принимаем.
Значения потенциалов П5 = 8 и П4 = 4 заносим в строку вершины 3 (табл. 13.8).
Из полученных значений потенциалов наименьшее у вершины 2 (П2 = 3), его выделяем, а вершину 2 переводим в первую группу. Смежные с вершиной 2 – вершины 7, 5, 3, вершину 1 во внимание не принимаем, она начальная. Потенциалы вершин, смежных с вершиной 2, П7 = 13; П5 = 7; П3 = 8. Потенциал П7 определен первый раз, его заносим в таблицу; потенциал П5 = 7 меньше, чем П5 = 8, следовательно П5 = 7 заносим в строку вершины 2, значение П5 = 8 в строке вершины 3 вычеркиваем; потенциал П3 = 8 больше, чем П3 = 2 в строке вершины 1; его во внимание не принимаем (табл. 13.9).
После этого вновь определяем вершину с наименьшим потенциалом (П4 = 4), переводим вершину 4 в первую группу и процесс повторяется. Результат расчета приведен в табл. 13.10.
Кратчайшие расстояния до всех вершин определены.