Смешанное произведение трех векторов.
Определение. Смешанным произведением трех векторов , , называется векторное произведение двух векторов , скалярно умноженное на третий вектор : (( ) )=( , , )
Смешанное произведение есть скалярная величина, по модулю численно равная объему параллелепипеда, построенного на этих векторах как на сторонах.
П
усть
=
,
тогда m=(
,
,
)=
=l
l
=
S ( H)= Vпараллелепипеда, где “+” означает, что , , образуют правую тройку, а “-“ –левую тройку. Отсюда получаем, что
Vпараллелепипедаl(
,
,
)l;
Vтетраэрда=
l(
,
,
)l.
Смешанное произведение векторов, заданных своими координатами.
Если перемножаемые векторы заданы их разложением по ортам:
=x1
+y1
+z1
,
=
x2
+y2
+z2
,
=x3
+y3
+z3
,
то их смешанное произведение будет равно определителю третьего порядка:
(
,
,
)=
.
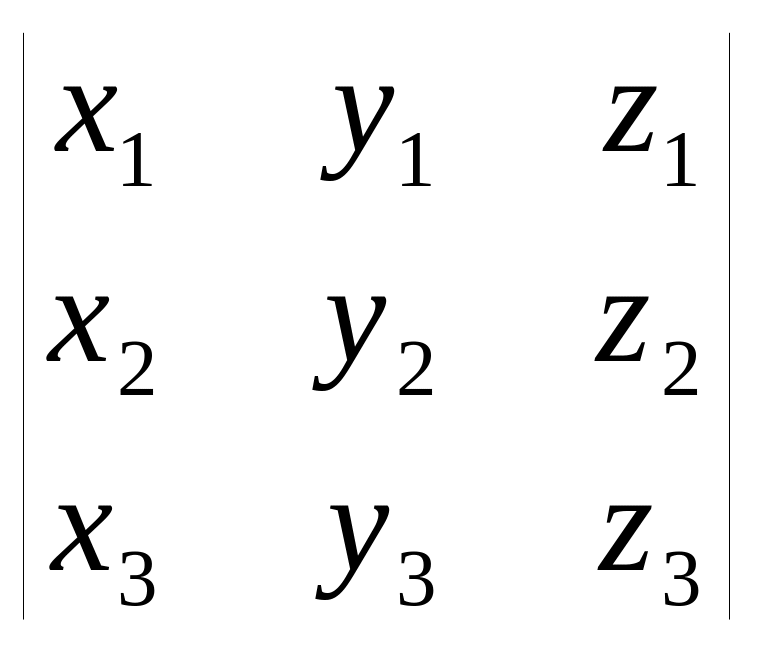Свойства смешанного произведения.
Если в смешанном произведении перемножаемые векторы переставить в круговом порядке, то произведение не изменится: ( ) =( ) =( ) .
Если в смешанном произведении поменять местами знаки векторного и скалярного умножения, то произведение не изменится: ( ) = ( ).
Это свойство позволяет записывать смешанное произведение в виде ( , , ) без знаков векторного и скалярного умножения.
Перестановка в смешанном произведении любых двух векторов изменит лишь его знак: = - ; = - ; = - .
Смешанное произведение обращается в нуль, если:
хотя бы один из перемножаемых векторов есть нуль- вектор;
б) два из перемножаемых векторов коллинеарные;
в) три перемножаемые вектора компланарны;
Заметим, что случай с) содержит в себе и оба предыдущих: Если хотя бы один из трех векторов есть нуль-вектор или два из них коллинеарны, то все три вектора будут компланарны, следовательно,
, , -компланарны. ( , , )=0 или =0.
Задачи по теме “Векторная алгебра”.
Задача 1. Дано: точки А(-3 1 2 ), В(4 –3 2 ), С(0 –1 3 ), D(-6 2 1 )
Найти: 1) координаты
и длину вектора
;
направляющие косинусы вектора
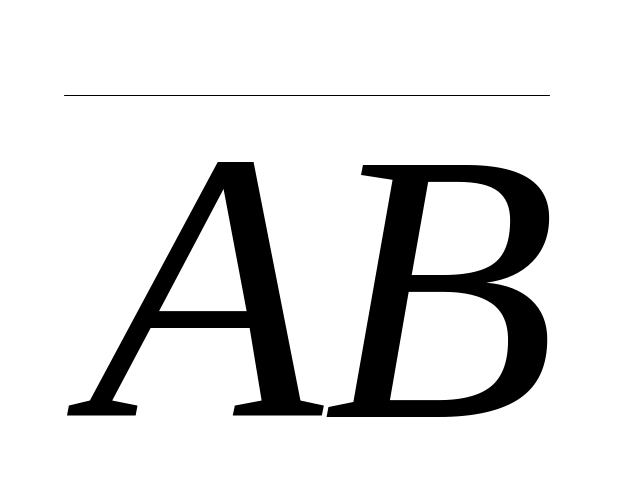;скалярное произведение
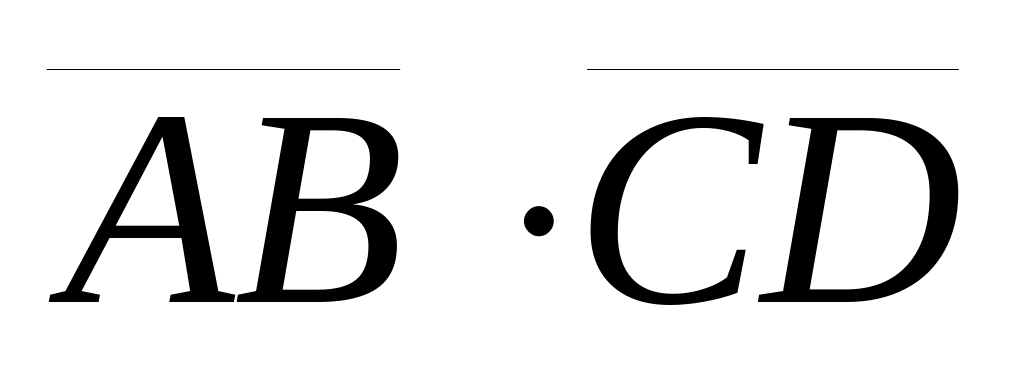;проекцию пр
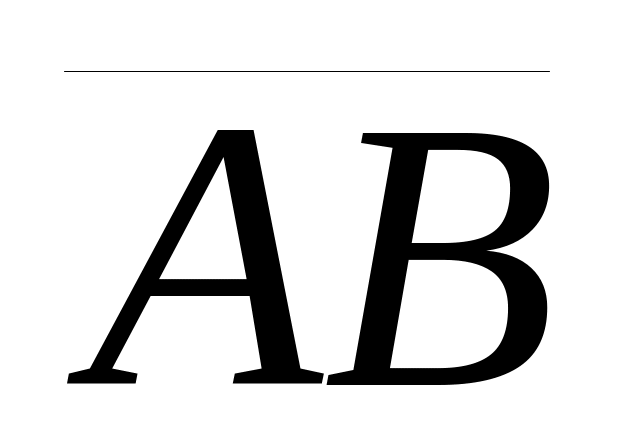.угол между векторами и
;векторное произведение и его модуль;
площадь треугольника АВC;
лежат ли точки А,В,С,D в одной плоскости;
объем пирамиды АВСD;
Решение. 1) Найдем координаты векторов и :
={4-(-3); -3-2; 2-2}, ={7; –4; 0}, ={-6-0; 2-(-1); 1-3}, ={-6; 3; –2}.
По правилам действий с векторами, получим
2 ={-12; 6; –4} и -2 ={7; –4; 0} - {-12; 6; –4} = {19; –10; 4}.
Теперь находим длину искомого вектора:
-2
=
=
.
2) Так как
={7;–4;
0 },
=
,
то направляющие косинусы находятся
согласно формулам:
cos
=
,
cos=
,
cos
=0.
3)
(
;
)
найдем по формуле скалярного произведения
векторов, заданных своими координатами.
Поскольку
={7;
–4; 0 },
={-6;
3; –2}, то
( ; )=7-6+(-4) 3+0(-2)=-54.
4) На основании формулы проекции, имеем
пр
=
.
Отсюда, пр
=
.
5) Заметим, что вектора ={7 –4 0 } и ={-6 3 –2} не являются коллинеарными, поскольку не пропорциональны их координаты:
.
Эти вектора не
являются также перпендикулярными, так
как их скалярное произведение
(
;
)
0.
Угол = ( ; ) найдем из формулы:
cos
=
.
Ранее
было найдено
(
)
= - 54,
,
,
стало быть,
cos
=
.
6) По формуле векторного произведения, имеем
=
=
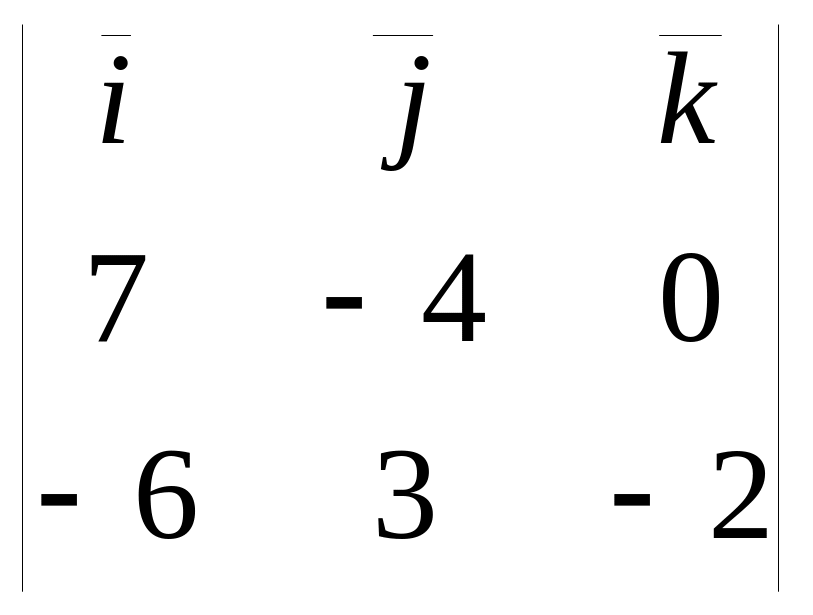=8
+14
-3
.
Таким
образом, векторное произведение имеет
координаты:
={8;
14; –3}, а его модуль
=
.
Применив формулу площади для треугольника ABC, построенного на векторах
,
,
получаем
.
Векторное
произведение
и его модуль найдем, аналогично решению
задачи 6):
=
,
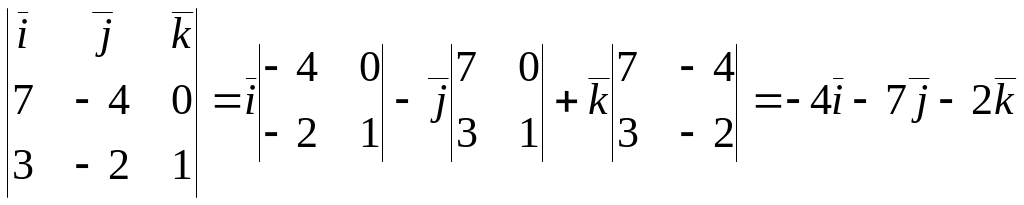={-4;
–7; –2},
=
.
Отсюда получаем,
что
(кв. ед.)
8) Точки A,B,C,D
будут лежать в одной плоскости, если
три вектора, соединяющие эти точки,
являются компланарными. Составим,
например, вектора
={7;
–4; 0},
={3;
–2; 1},
={-3;
1; –1} и найдем их смешанное произведение:
(
;
;
)=
,
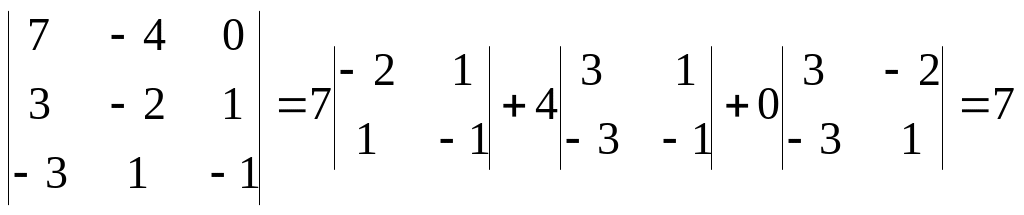Поскольку ( ; ; ) 0, то вектора , , не компланарны, а стало быть, точки A,B,C,D не лежат в одной плоскости.
Т
ак
как объем пирамиды равен
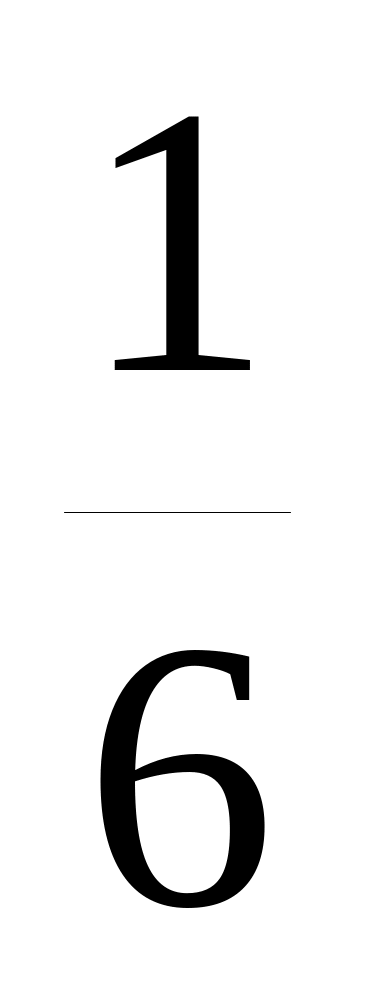части
объема параллелепипеда, построенного
на векторах
,
,
вычисляется по формуле
Vпирамиды=
Vпараллелепипеда
,
A
С то используя решение
задачи 8), получим Vпир=
(куб.ед.)
.
Задача 2. Определить
при каких
вектора
и
коллинеарны.
Решение. В случае
коллинеарности, соответствующие
координаты векторов
={-2;3;
}
и
={
;
-6; 2} должны быть пропорциональны, то
есть:
.
Отсюда
=4
и
=-1
Задача 3.
Определить при каком
вектора
и
перпендикулярны.
Решение. Вектора
={3;–2;
}
и
={1;3;-1}
перпендикулярны, если их скалярное
произведение
равно нулю. Из этого условия получаем:
=
=0.
Стало быть,
=-3.
Задача 4.
Вычислить, какую работу производит сила
{5
2 1}, когда точка ее приложения перемещается
из A(3;
0; 3) в B(-4;
1; 2).
Образуем
вектор перемещения
={-7;
1; -1}.
A
B
Тогда работа A=
=
-34.
Задача 5.
Найти
,
если
=1,
=3,
=
.
Решение. В силу свойств скалярного произведения, имеем:
=2
+6
-
-3
=2
2+5
-3
2=2
2+5
cos
--3
2.
Подставляя теперь в правую часть данные задачи, получим = -17,5.
Задача 6. Сила {5;–3; -7} приложена в точке В(2;1;1). Определить момент силы относительно точки К(2; 3; 4).
Решение. Образуем
вектор
={0
–2 -3}. Тогда момент относительно точки
К вычисляется по формуле:
=momK
=
.
Имеем,
=
,
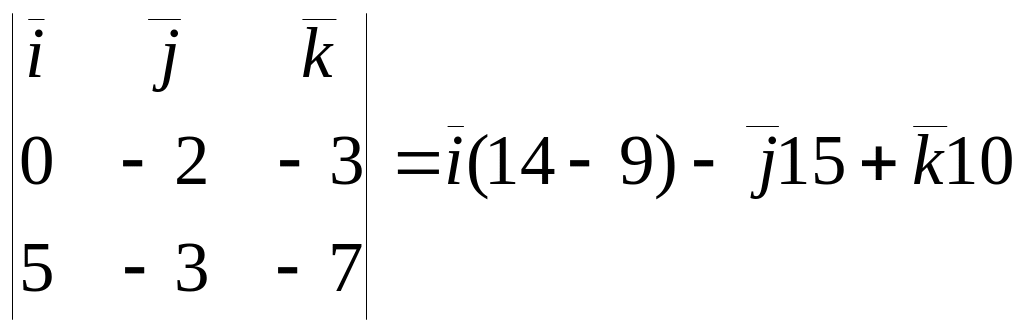или
={5;
–15; 10}.
Задача 7.
Найти
,
если
,
=1,
=3,
=
.
Решение. Используя
свойства векторного произведения,
упростим конструкцию вектора
,
а именно:
=2
- 8
+
- 4
.
Так как II , II , то = =0. Следовательно,
= - 8 + = - 9 .
Теперь по формуле модуля векторного произведения, получаем
=I - 9 I=9I I=9 sin =27 sin =13,5.