Экспериментальная часть

Приборы и оборудование: источник питания ИП; преобразователь импульсов ПИ; звуковой генератор PQ; осциллограф PO; магазин емкостей МЕ; модуль ФПЭ-13.

Функциональная схема представлена на рис. 10.5.

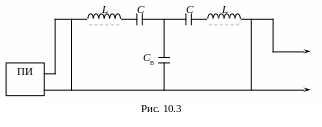
М етодика измерений

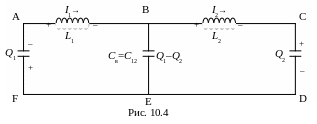
Для теоретических расчетов рассмотрим упрощенный вариант этой схемы – рис. 10.4, где обозначены знаки зарядов с обкладок конденсаторов в контурах и положительное направление тока: С_в=С₁₂; L₁=L₂=L, причем для наблюдения биений важно, чтобы I₁ и I₂ были сонаправлены. При одинаковом направлении токов знаки зарядов конденсаторов С₁ и С₂ окажутся такими, как указано на рис.10.4, а при равенстве этих зарядов конденсатор С₁₂ окажется незаряженным. Таким образом, если в начальный момент Q₁=Q₂, то колебания в контурах будут происходить независимо, так как конденсатор С₁₂ никакого влияния на колебания оказывать не будет. Такая ситуация аналогична колебаниям, возникающим в связанных математическиз маятниках, изображенных на рис.10.1,а.

Для двух LC – контуров, соединенных по схеме, показанной на рис. 10.4, запишем второе правило Кирхгофа для контуров ABEF и BCDE:

, (10.1)

. (10.2)

Подставляя , получаем:

; (10.3)

. (10.4)

Получилось довольно сложные уравнения для двух переменных. Можно упростить ситуацию, написать новые уравнения, полученные сложением и вычитанием уравнений (10.3) и (10.4).

Сложив эти уравнения, получаем:

. (10.5)

Разность (10.3) и (10.4) имеет вид:

. (10.6)

В (10.5) и (10.6) учтено, что С₁=С₂=С. Введём новые переменные:

и (10.7)

и обозначим:

и , (10.8)

тогда в новых переменных (10.5) и (10.6) будут выглядеть так:

, (10.5а)

. (10.6а)

С помощью проведенных математических операций удалось свести уравнения (10.3) и (10.4) к более простым уравнениям относительно переменных и .

Если при t=0 переменная имеет значение , то решение уравнения (10.5а) имеет вид

(10.9)

частота

(10.10)

равна частоте собственных колебаний отдельного контура. Аналогично, решение уравнения (10.6а) приобретает вид:

(10.11)

где

; (10.12)

– значение при t=0 переменной .

Два вида движения, описываемые уравнениями типа (10.5а) и (10.6а), называются нормальными модами колебаний системы связанных контуров, а переменные и – нормальными переменные. В данном случае эти уравнения описывают колебания тока в системе двух связанных электрических контуров. Нормальная мода колебаний – это коллективное колебание, при котором амплитуда колебаний каждого заряда и тока остается неизменной. Дифференциальные уравнения колебаний, записанные в нормальных переменных, имеют наиболее простой вид – это однородные дифференциальные уравнения второго порядка. Их решениями являются гармонические функции. Соответствующие частоты таких колебаний также называются нормальными.

Если вывести из положения равновесия один из контуров например, зарядить конденсатор С₁), то результирующим колебанием будет наложение (суперпозиция) двух нормальных мод колебаний. При Q₂₀=0 из (10.7), (10.9) и (10.10) получаем:

; (10.11)

. (10.12)

Используя известные тригонометрические тождества:

;

,

можно записать уравнения (10.11) и (10.12) в виде:

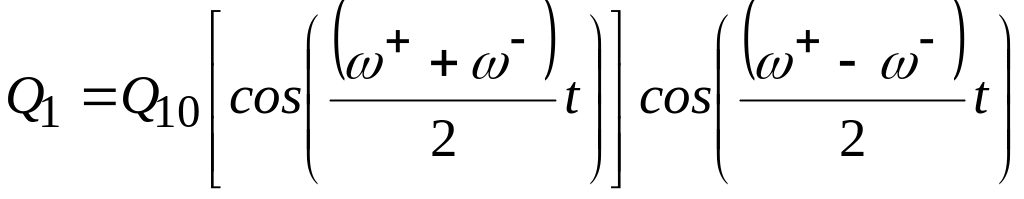; (10.13)

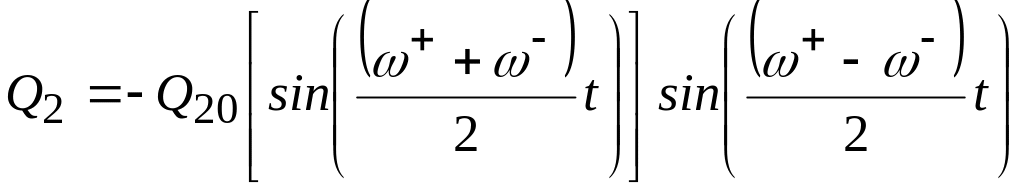. (10.14)

Вид функций Q₁(t) и Q₂(t) (10.13) и (10.14) для случая слабой связи между контурами ( <<1) показан на рис. 10.2. В этом случае нормальные частоты и близки друг другу (10.10) и (10.12), и вторые сомножители в (10.13) и (10.14) изменяются достаточно медленно по сравнению с первыми, так как разность мала по сранению с суммой . Получается амплитудно-модулированный сигнал с амплитудой, изменяющейся с периодом (период биений) и основной частотой, совпадающей с резонансной частотой колебаний каждого контура – . При t=0 амплитуда Q₂ равна нулю. Затем амплитуда Q₂ увеличивается, а амплитуда Q₁ уменьшается до тех пор, пока в момент времени, определяемый из соотношения амплитуда Q₁ не станет минимальной, а амплитуда Q₂ достигнет максимума.

Ситуацию, показанную на рис. 10.2, можно рассмотреть с энергетической точки зрения. При t=0 вся энергия сосредоточена в контуре 1. В результате связи через емкость С₁₂ энергия постепенно передается от контура 1 к контору 2 до тех пор, пока вся энергия не соберется в контуре 2. Время, необходимое для перехода энергии из контура 1 в контур 2 и обратно, можно получить из уравнения , а частота, с которой контуры обмениваются энергией

(10.15)

Для четной моды колебаний, обозначенной знаком «+», токи текут в одинаковом направлении и на емкости С₁₂ нет заряда. При этом частота ω⁺ остается такой же, как для несвязанных контуров, т.е. . В случае нечетной моды нормальных колебаний (знак «–»), емкость С₁₂ заряжена, что увеличивает частоту колебаний, т.е. .

Следует отметить, что для того, чтобы применить к связанным контурам рассмотренную выше теорию, они должны иметь одинаковую резонансную частоту и, кроме того, предполагается, что С₁₂ велика по сравнению с С, то есть <<1 («слабая связь»). Тогда выражение 10.15 можно преобразовать следующим образом

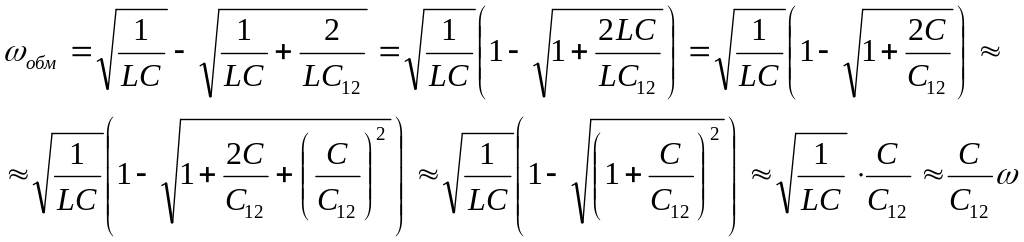(10.16)

Полученное значение частоты обмена ω_обм (имеется в виду обмен энергией), или частоты “биений” ω_б=ω_обм можно изменять, настраивая систему контуров путем изменения номиналов элементов С, С₁₂, L, R и т.д., добиваясь того, чтобы разностная частота была сведена к минимуму.

Исследование биений, то есть обмена энергий в связанных контурах, и является одной из практических задач данной лабораторной работы.