4. Обчислення границі функції в точці.
Доводити, що число є границею функції у точці з одного боку складно, з іншого не завжди можливо наперед знати границю. Тому виникає проблема обчислення границь конкретних елементарних функцій у заданих точках. Для розв’язання цієї задачі використовують основні формули, які доводяться на основі теорем про границі.
1.
(4.1)
2.
(4.2)
3.
(4.3)
4.
(4.4)
5.
(4.5)
Формули (4.1) – (4.5)
мають місце за умови, коли границі
існують і не дорівнюють нескінченності.
4.1. Границі многочлена та дробово-раціональної функції у точці.
Теорема 9
Границя многочлена
у точці дорівнює значенню многочлена
у цій точці, тобто
,
де
Для доведення використовують основні
формули та теорему 1 (
).
Теорема 10
Границя раціональної
функції
,
де
– многочлени, у точці а
дорівнює значенню цієї функції у точці,
тобто
,
якщо
.
Доведення проводимо, використовуючи основні формули та теорему 9.
Приклад 2
Знайти границю:
Розв’язання.
Використаємо
теорему 10 і одержимо:
Приклад 3
Знайти границю:
.
Розв’язання.
При знаходженні
цієї границі ми не можемо використати
теорему 10, бо границя знаменника дорівнює
нулю. Підстановка числа
під знак границі приводить до невизначеності
типу
.
Для обчислення границі розкладаємо
чисельник та знаменник на множники і
скорочуємо на
:
=
=
.
Зауваження.
Якщо х=а
– корінь многочлена
,
тобто
,
то за наслідком теореми Безу
ділиться без остачі на
,
тому його можна розкласти на множники:
,
де
– многочлен.
Приклад 4
Знайти границю:
.
Розв’язання.
=
.
4.2. Границі тригонометричних функцій. Перша важлива границя.
Теорема 11
.
Теорема 12
.
Теорема 13
.
Цю границю називають першою важливою границею.
Приклади 5 – 8
Знайти границі.
5.
6.
7.
8.
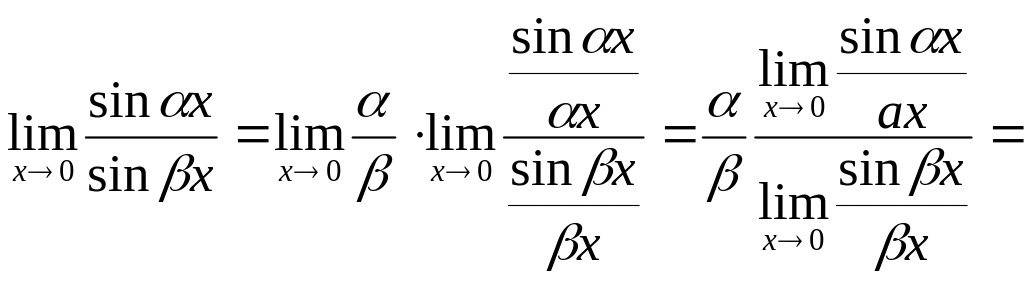
Теорема 14
.
Теорема 15
.
Приклади 9 – 10
Знайти границі.
9.
.
10.
Означення 3.
Дві
нескінченно малі функції називаються
еквівалентними, якщо
Позначаються
.
Розглянуті приклади дозволяють записати такі еквівалентні нескінченно малі функції:
.
При знаходженні границь доцільно нескінченно малі функції заміняти еквівалентними.
Приклад 11
Знайти границю:
;
Розв’язання.
=
=
= =
=
4.3. Друга важлива границя.
Означення 4.
Границя
змінної величини
при
називається числом е (
– ірраціональне число).
Теорема 15
Друга важлива
границя.
,
або
.
Друга важлива
границя використовується при розкритті
невизначеності типу
.
Приклад 12
Знайти границю:
Розв’язання.
=
=
=
=
=
=
.
Для розкриття
невизначеності типу
використовують простий прийом:
=
.
Приклад 13
Знайти границю:
Розв’язання.
=
=
=
=
4.4. Границі показникових та логарифмічних функції.
Теорема 16
.
Теорема 17
,
.
Приклад14
Знайти границю:
Розв’язання.
=
=
=
=
=
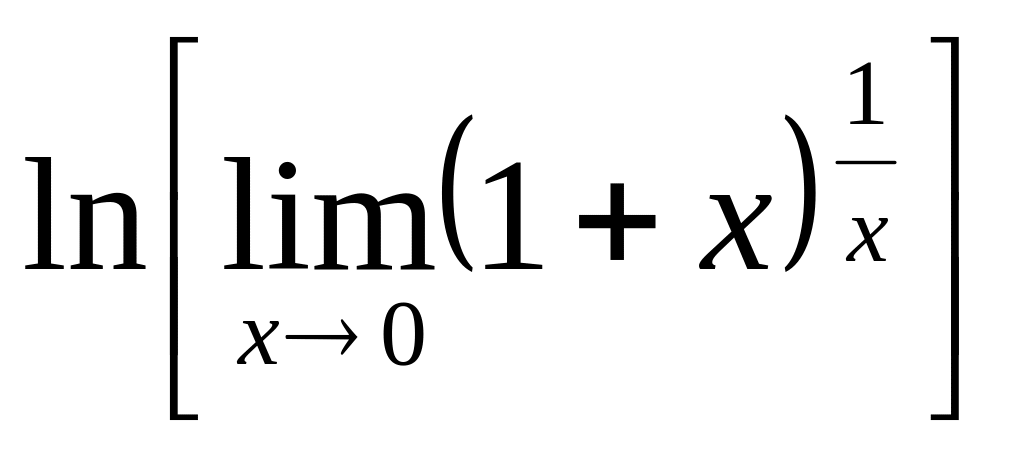Приклад 15
Знайти границю:
Розв’язання.
=
.
Зауваження.
Приклади 14 і 15 дають ще дві еквівалентні
нескінченно малі, які доцільно
використовувати при обчисленні границь.
.
4.5. Границі ірраціональних функцій.
Теорема 18
,
.
Приклад 16
Знайти границю:
.
Розв’язання.
=
=
=
=
=
4.6. Границя функції на нескінченності.
Означення 14.
Число А
називається границею функції
,
коли
,
якщо для будь-якого додатного числа
існує таке додатне число М,
що із нерівності
випливає
нерівність
.
Аналогічно означають
границю, коли
.
Запишемо поведінку відомих елементарних функцій на нескінченності.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10. Границі
тригонометричних функцій
на
нескінченності не існують.
Теорема 19
=
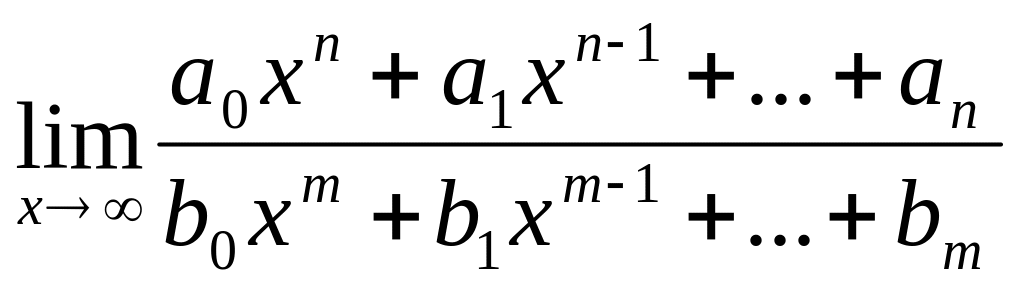Приклад 17
Знайти границю:
.
Розв’язання.
=
(використано теорему 19)
Приклад 18
Знайти границю:
.
Розв’язання.
=
(використано
теорему 19)
Приклад 19
Знайти границю:
Розв’язання.
=
(використано
теорему 19)
ІІІ. Неперервність функцій.
1. Означення неперервності.
Означення 5
Функція
називається
неперервною в точці
,
якщо:
функція визначена в точці і деякому її околі;
ця границя дорівнює значенню функції в точці , тобто
=
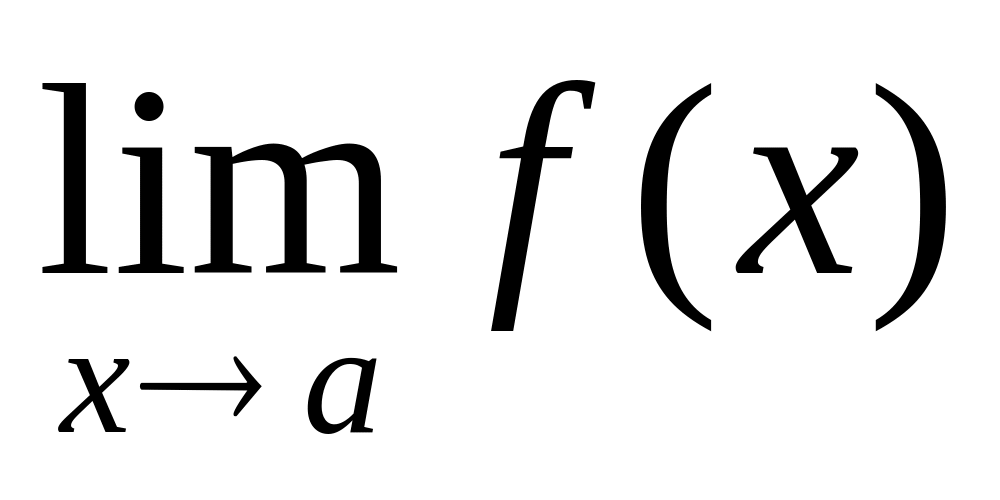Зауваження 1.
З умови неперервності випливає, що
=
.
Це дає правило граничного переходу під знаком неперервної функції.
Зауваження 2.
Умова неперервності може також бути
представлена в вигляді:
Ця умова означає,
що для неперервної в точці
функції, границя функції справа в точці
дорівнює границі функції зліва в точці
і дорівнює значенню функції в цій точці.