
- •1. Аксиоматика 3
- •2. Множества 4
- •3. Аналитическая геометрия 14
- •4. Векторная алгебра 25
- •5. Матрицы и определители 30
- •Аксиоматика
- •Аксиоматический метод построения математики
- •Математический язык
- •Множества
- •Понятие множества
- •Пустое множество
- •Числовые множества
- •Подмножества
- •Пересечение множеств
- •Объединение множеств
- •Вычитание множеств
- •Аналитическая геометрия
- •Система координат на плоскости и в пространстве
- •Расстояние между двумя точками на плоскости
- •Уравнение линии. Уравнение прямой с угловым коэффициентом
- •Уравнение – уравнение прямой с угловым коэффициентом k
- •Общее уравнение прямой
- •Уравнение прямой в отрезках
- •Уравнение прямой, проходящей через данную точку в данном направлении
- •Уравнение прямой, проходящей через данную точку
- •Уравнение прямой, проходящей через две данные (различные) точки и
- •Полярные координаты
- •Угол между прямыми
- •Уравнение окружности
- •Эллипс. Каноническое уравнение эллипса
- •Гипербола. Каноническое уравнение гиперболы
- •Парабола. Каноническое уравнение параболы
- •У равнение сферы
- •Векторная алгебра
- •Понятие вектора
- •Коллинеарные векторы
- •Операции над векторами
- •Угол между векторами
- •Проекция вектора на ось
- •Скалярное произведение двух векторов
- •Координаты вектора
- •Разложение векторов
- •Действия над векторами, заданным координатами в пространстве
- •Матрицы и определители
- •Матрицы
- •Определители
- •Определители третьего порядка
- •Миноры и алгебраические дополнения матрицы
- •Обратная матрица
- •Системы линейных уравнений
- •Формулы Крамера
- •Матричный способ решения систем линейных уравнений
- •Метод Гаусса
- •Функции
- •Понятие функции
- •Способы задания функции
- •Обзор элементарных функций и их графиков
- •Пределы
- •Предел последовательности
- •Предел функции
- •Непрерывность функции
- •Производная
- •Определение производной
- •Правила дифференцирования
- •Производные высших порядков
- •Применение производной для исследования функции
- •Неопределенный интеграл
- •Способы интегрирования
- •О пределенный интеграл
- •Дифференциальные уравнения
- •Основные понятия:
- •Признаки сходимости ряда:
- •Ряды по степени разности
- •Теория вероятностей
- •Основные понятия теории вероятностей
- •Классическое определение вероятности
- •Геометрические вероятности
- •Алгебра событий
- •Теорема сложения вероятностей двух несовместимых событий
- •Теорема умножения вероятностей.
- •Теорема сложения вероятностей совместимых событий
- •Формула полной вероятности
- •Теорема умножения вероятностей независимых событий:
- •Дискретные случайные величины
- •Закон распределения дискретных случайных величин
- •Функция распределения случайной величины
- •Нормальное распределение
- •Числовые характеристики случайных величин
- •Свойства математического ожидания (мо) дискретной случайной величины:
- •Дисперсия дискретной случайной величины
- •Среднее квадратичное отклонение (стандартное)
- •Системы двух случайных величин и их числовые характеристики
- •Литература
Дифференциальные уравнения
Определение:
дифференциальным
уравнением
называется соотношение, связывающее
независимую переменную x,
искомую функцию
![]() и ее производные. Если искомая функция
есть функция одной независимой
переменной, то дифференциальное
уравнение называется обыкновенным.
и ее производные. Если искомая функция
есть функция одной независимой
переменной, то дифференциальное
уравнение называется обыкновенным.
Всякая
функция
![]() ,
которая, будучи подставлена в уравнение,
обращает его в тождество, называется
решением
этого уравнения.
Решение уравнения, содержащее произвольную
постоянную величину, имеет вид
,
которая, будучи подставлена в уравнение,
обращает его в тождество, называется
решением
этого уравнения.
Решение уравнения, содержащее произвольную
постоянную величину, имеет вид
![]() .
.
Дифференциальное
уравнение первого порядка имеет вид:
![]() или
или
![]() .
Например:
.
Например:
![]() ;
;
![]() .
.
Порядком
(рангом)
дифференциального уравнения является
порядок старшей производной входящей
в него. Общий вид дифференциального
уравнения
-го
порядка следующий:
![]() .
.
Общим
решением
дифференциального уравнения
-го
порядка называется функция
![]() ,
существенно зависящая от
произвольных постоянных и обращающая
данное уравнение в тождество при любых
значениях этих постоянных.
,
существенно зависящая от
произвольных постоянных и обращающая
данное уравнение в тождество при любых
значениях этих постоянных.
Уравнение
вида
![]() ,
где
,
где
![]() и
и
![]() –
постоянные действительные числа
называется линейным однородным
дифференциальным уравнением второго
порядка с постоянными коэффициентами.
Его решение имеет вид функции
–
постоянные действительные числа
называется линейным однородным
дифференциальным уравнением второго
порядка с постоянными коэффициентами.
Его решение имеет вид функции
![]() .
Дифференцируя ее, имеем
.
Дифференцируя ее, имеем
![]() ,
,
![]() .
Уравнение, получаемое при подстановке
в условие значений
.
Уравнение, получаемое при подстановке
в условие значений
![]() и
и
![]() ,
имеет вид
,
имеет вид
![]() – называется
характеристическим
уравнением данного дифференциального
уравнения.
– называется
характеристическим
уравнением данного дифференциального
уравнения.
Решить,
или проинтегрировать, данное
дифференциальное уравнение – значит
найти его
общее решение, которое имеет вид:
![]() .
Решение, которое получается из общего
решения при некотором фиксированном
значении произвольной постоянной С,
называется частным
решением:
если при
.
Решение, которое получается из общего
решения при некотором фиксированном
значении произвольной постоянной С,
называется частным
решением:
если при
![]() ,
,
![]() ,
то такие условия называются начальными.
,
то такие условия называются начальными.
Простейшие классы дифференциальных уравнения:
 ,
тогда
,
тогда
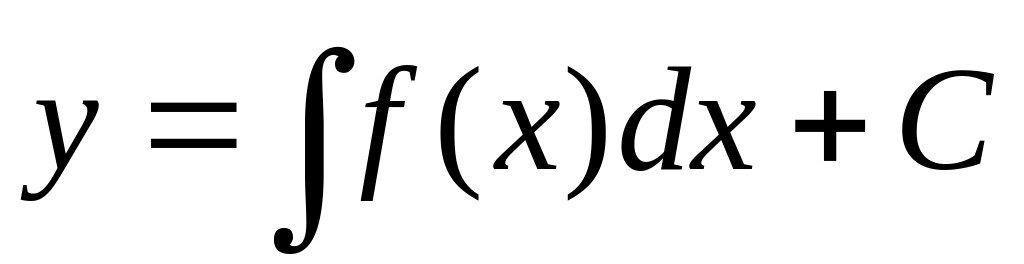 если данный интеграл берется, то
уравнение интегрируется в элементарных
функциях.
если данный интеграл берется, то
уравнение интегрируется в элементарных
функциях.
Уравнение вида
 (правая часть не содержит х).
Т.к.
(правая часть не содержит х).
Т.к.
 ,
то
,
то
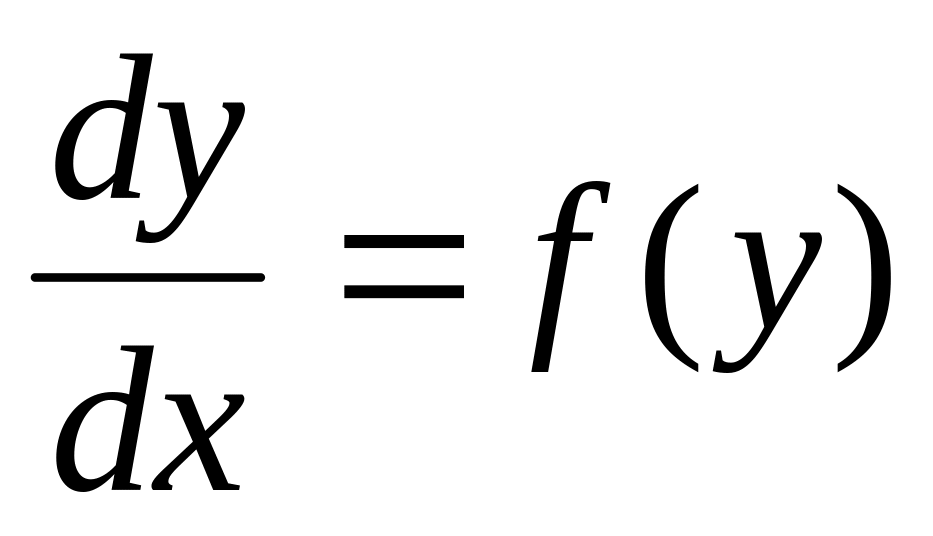 ,
,
 .
Интегрируя обе части имеем:
.
Интегрируя обе части имеем:
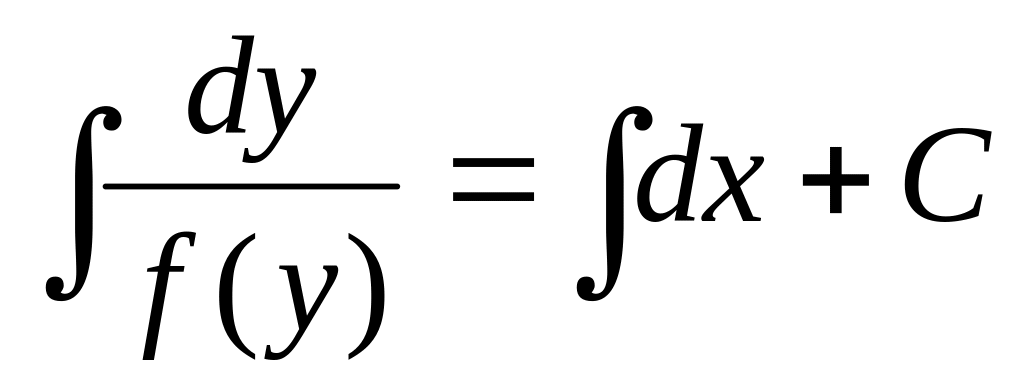 или
или
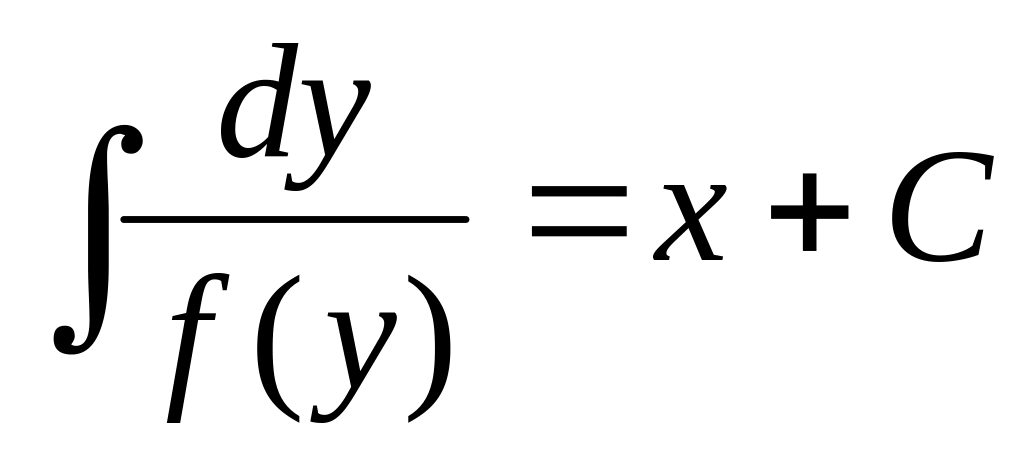 (могут быть потеряны корни
(могут быть потеряны корни
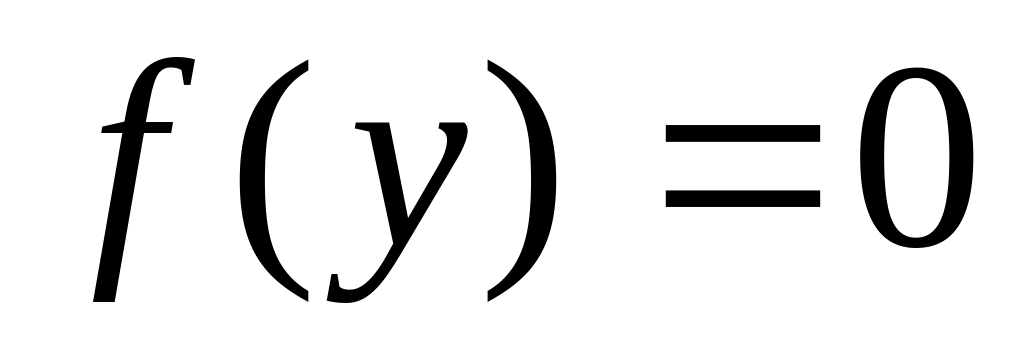 ).
).Уравнение с разделенными переменными, т.е. уравнение вида:
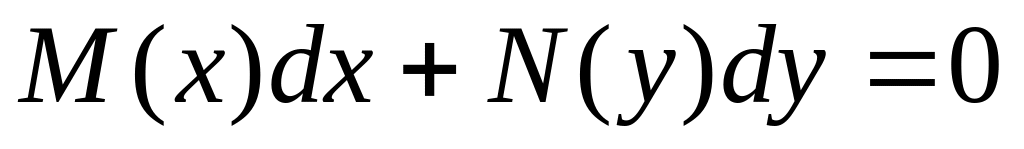 ,
или
,
или
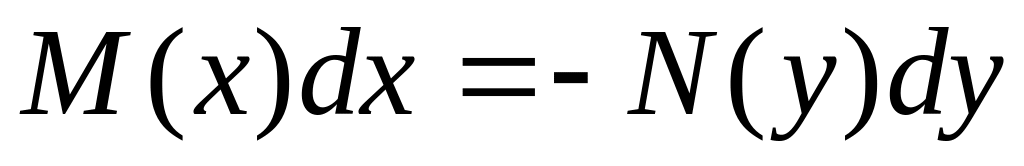
![]()
![]()
Уравнение с разделяющимися переменными имеет вид: или
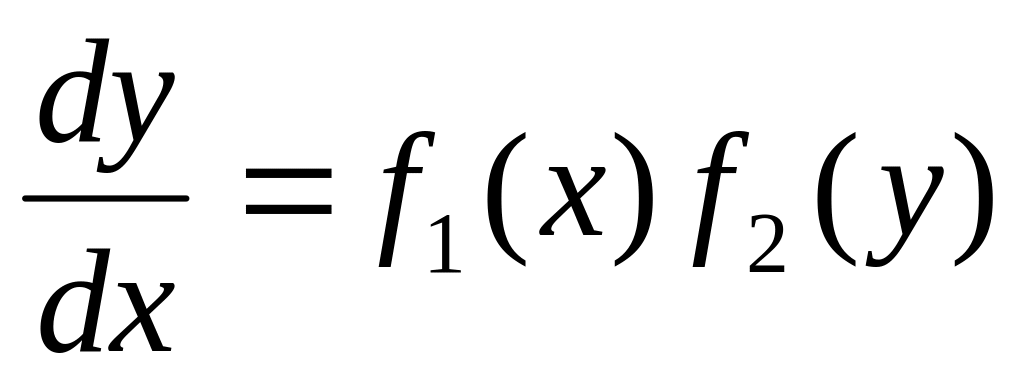 .
Его можно записать виде:
.
Его можно записать виде:
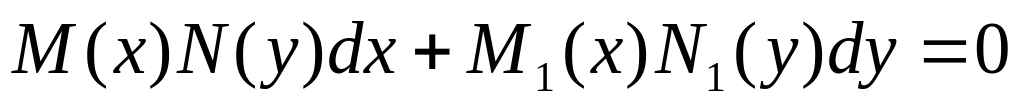 .
.
Ряды
Основные понятия:
Определение
1.
Математическое выражение
![]() называется числовым рядом, или просто
рядом, а числа
называется числовым рядом, или просто
рядом, а числа
![]() называются членами ряда. Применяется
и запись:
называются членами ряда. Применяется
и запись:
![]() .
.
Ряд
считается заданным, если известен общий
член
![]() .
.
Сумма
конечного числа членов ряда
![]() ,
,
![]() ,
,
![]() и т.д. называются частными
суммами (отрезками) ряда.
и т.д. называются частными
суммами (отрезками) ряда.
Рассмотрим
последовательность
![]() .
.
Определение
2. Если
существует предел
![]() ,
то ряд называется сходящимся,
а число S
– суммой этого ряда.
,
то ряд называется сходящимся,
а число S
– суммой этого ряда.
Если эта последовательность не имеет предела, то ряд называется расходящимся.
Расходящийся ряд суммы не имеет.
Признаки сходимости ряда:
Если
ряд
сходится, то общий член
![]() стремится к нулю при неограниченном
возрастании n,
т.е.
стремится к нулю при неограниченном
возрастании n,
т.е.
![]() (это необходимый признак сходимости
ряда).
(это необходимый признак сходимости
ряда).
Если
общий член ряда не стремится к нулю, то
ряд расходится при
![]() .
.
Признак
Даламбера:
если для положительного ряда существует
![]() ,
то при
,
то при
![]() ряд сходится, а при
ряд сходится, а при
![]() – расходится.
– расходится.
Числовые ряды бывают знакопостоянные и знакопеременные: если все члены ряда только положительные, то это знакоположительный ряд; если все члены – отрицательные, то это знакоотрицательный ряд; если не все члены имеют одинаковые знаки, то это знакопеременный ряд.
Ряд,
членами которых являются функции
![]() ,
называются функциональными.
Пример:
,
называются функциональными.
Пример:
![]() .
.
Если
в функциональном ряде придать
значение
,
то ряд
![]() будет числовым.
будет числовым.
Степенными
рядами
называются функциональные ряды вида
![]() ,
где
,
где
![]() – постоянные числа, называемые
коэффициентами степенного ряда.
– постоянные числа, называемые
коэффициентами степенного ряда.
Пример:
![]() .
Этот ряд сходится лишь при
.
При всех
.
Этот ряд сходится лишь при
.
При всех
![]() этот ряд расходится. Такой ряд относится
к рядам первого
класса.
этот ряд расходится. Такой ряд относится
к рядам первого
класса.
Есть
степенные ряды, которые сходятся на
всей числовой оси. Такие ряды относятся
к рядам второго
класса.
Например, ряд
![]() сходится на всей числовой оси:
сходится на всей числовой оси:
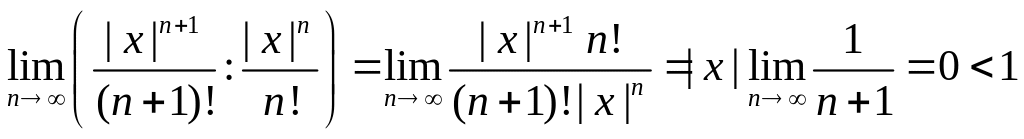
Ряды, которые не принадлежат к рядам первого и второго классов, относятся к рядам третьего класса.
Например
ряд
![]() ;
;
![]() есть ряд третьего класса, т.к.
есть ряд третьего класса, т.к.
![]() .
.
Определение:
такое число
,
что степенной ряд
![]() сходится при
сходится при
![]() и расходится при
и расходится при
![]() называется радиусом
сходимости.
Для рядов первого класса
называется радиусом
сходимости.
Для рядов первого класса
![]() ;
для ряда второго класса
;
для ряда второго класса
![]() .
.
Если
для ряда
![]() существует и отличен от нуля предел
существует и отличен от нуля предел
 ,
то
,
то
![]() .
В примере, рассмотренном выше,
.
В примере, рассмотренном выше,
![]() ,
а областью сходимости
,
а областью сходимости
![]() .
.
