9. Неопределенный интеграл

Определение 1: операция, обратная дифференцированию, называется интегрированием.

Если есть функция заданная для тех же значений, что и выполняется условие, что , то – первообразная функция.

Определение 2: выражение , где первообразная функции и – произвольная постоянная, называется неопределенным интегралом от функции : , где – подынтегральная функция; – подынтегральное выражение; – переменная интегрирования, – знак интеграла.

, если .

Таблица основных интегралов

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

1. Способы интегрирования

1. Непосредственное интегрирование:

2. Замена переменной интегрирования. Интегрирование путем ведения новой переменной (метод подстановки основан на формуле , где – функция переменной .

3. Интегрирование по частям. Если , – дифференцируемые функции от , то из формулы дифференциала произведения двух функций 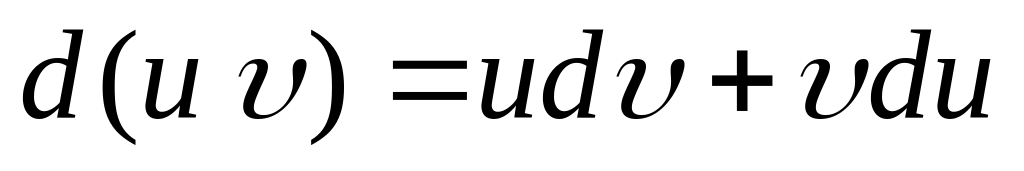получается формула интегрирования по частям:

В качестве обычно выбирается функция, которая упрощается дифференцированием, в качестве – оставшаяся часть подынтегрального выражения, содержащая , из которой можно определить путем интегрирования.

10. О пределенный интеграл

П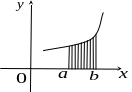 усть на отрезке определена функция . Отрезок разобьем на частей точками . В каждом из отрезков произвольным образом выберем точку и составим сумму произведений

Эта сумма называется интегральной суммой функции в промежутке .

Определение: определенным интегралом от функции в промежутке называется предел ее интегральной суммы, когда число элементарных отрезков неограниченно возрастает, а длинна наибольшего из них стремится к 0.

– подынтегральное выражение; и – пределы интегрирования ( – нижний, – верхний), – интегральная сумма.

1. Свойства определенного интеграла

1. ;

2. ;

3. ;

4. 

2. Формула Ньютона-Лейбница

Если – первообразная на , то

Пример:

1. 

2. 

3. Геометрический смысл определенного интеграла:

Определенный интеграл представляет собой площадь криволинейной трапеции, ограниченной сверху линией , снизу прямой , слева прямой и справа прямой .

Если фигура ограничена линиями и , , и , при условии, что то .

11. Комбинаторика

Комбинаторикой называется раздел математики, изучающий вопрос о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).

Определение 1. Множества элементов, состоящие из одних и тех же различных элементов и отличающиеся друг от друга их порядком, называются перестановками этих элементов.

(пэ из эн есть эн-факториал)

.

Принимается, что .

Определение 2. Размещениями из n различных элементов по m называют множества, содержащие m элементов из числа n заданных, и которые отличаются либо составом элементов, либо их порядком. Обозначается (читается A из эн по эм).

.

Определение 3. Сочетаниями из n различных элементов по m, называются множества, содержащие m элементов из числа n заданных, и которые отличаются хотя бы одним элементом.

Записывается: (читается цэ из эн по эм),

Замечание: .

Отметим разницу между сочетаниями и размещениями: в сочетаниях не учитывается порядок элементов.

Правило сумм: если некоторый объект А может быть выбран из множества объектов m способами, а объект В – n способами, то выбрать либо А, либо В можно способами.

Правило произведения: если объект А может быть выбран из множества объектов m способами и после каждого такого выбора объект B может быть выбран n способами, то пара объектов в указанном порядке может быть выбрана способами.