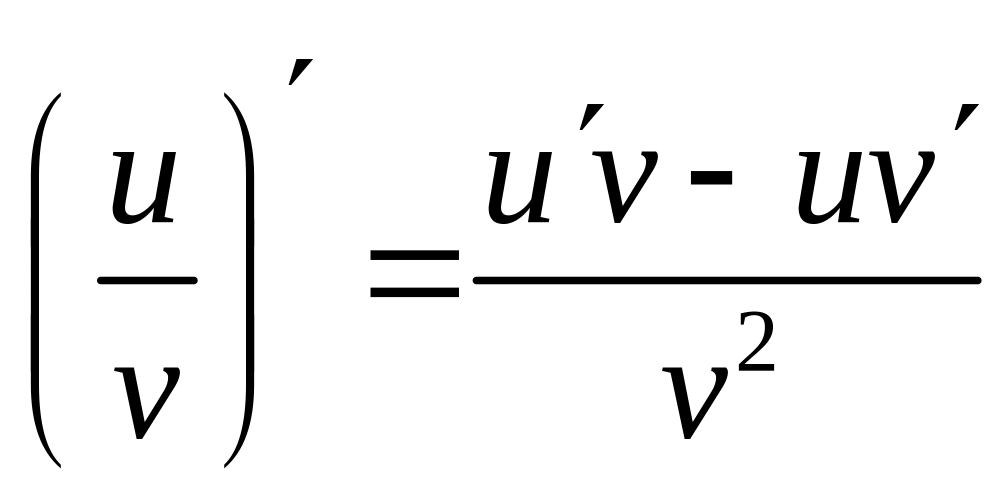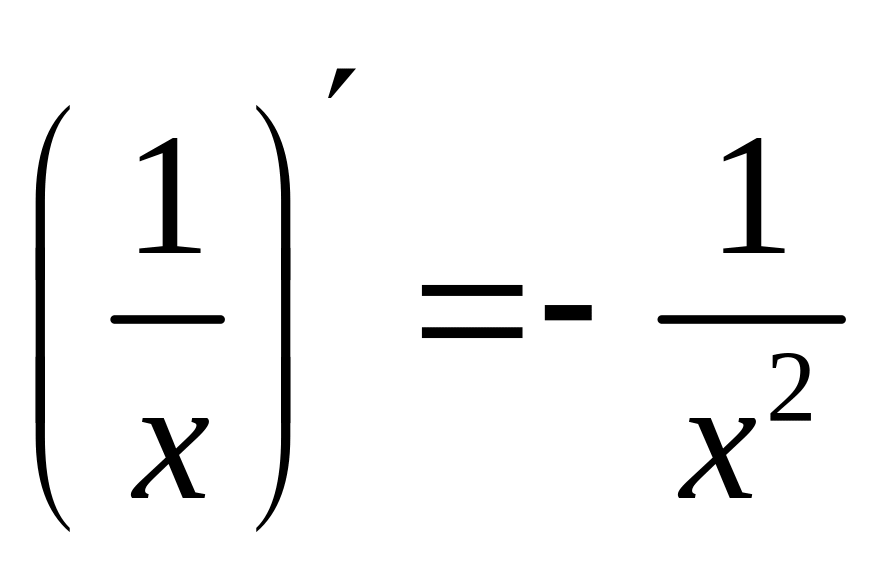- •1. Аксиоматика 3
- •2. Множества 4
- •3. Аналитическая геометрия 14
- •4. Векторная алгебра 25
- •5. Матрицы и определители 30
- •Аксиоматика
- •Аксиоматический метод построения математики
- •Математический язык
- •Множества
- •Понятие множества
- •Пустое множество
- •Числовые множества
- •Подмножества
- •Пересечение множеств
- •Объединение множеств
- •Вычитание множеств
- •Аналитическая геометрия
- •Система координат на плоскости и в пространстве
- •Расстояние между двумя точками на плоскости
- •Уравнение линии. Уравнение прямой с угловым коэффициентом
- •Уравнение – уравнение прямой с угловым коэффициентом k
- •Общее уравнение прямой
- •Уравнение прямой в отрезках
- •Уравнение прямой, проходящей через данную точку в данном направлении
- •Уравнение прямой, проходящей через данную точку
- •Уравнение прямой, проходящей через две данные (различные) точки и
- •Полярные координаты
- •Угол между прямыми
- •Уравнение окружности
- •Эллипс. Каноническое уравнение эллипса
- •Гипербола. Каноническое уравнение гиперболы
- •Парабола. Каноническое уравнение параболы
- •У равнение сферы
- •Векторная алгебра
- •Понятие вектора
- •Коллинеарные векторы
- •Операции над векторами
- •Угол между векторами
- •Проекция вектора на ось
- •Скалярное произведение двух векторов
- •Координаты вектора
- •Разложение векторов
- •Действия над векторами, заданным координатами в пространстве
- •Матрицы и определители
- •Матрицы
- •Определители
- •Определители третьего порядка
- •Миноры и алгебраические дополнения матрицы
- •Обратная матрица
- •Системы линейных уравнений
- •Формулы Крамера
- •Матричный способ решения систем линейных уравнений
- •Метод Гаусса
- •Функции
- •Понятие функции
- •Способы задания функции
- •Обзор элементарных функций и их графиков
- •Пределы
- •Предел последовательности
- •Предел функции
- •Непрерывность функции
- •Производная
- •Определение производной
- •Правила дифференцирования
- •Производные высших порядков
- •Применение производной для исследования функции
- •Неопределенный интеграл
- •Способы интегрирования
- •О пределенный интеграл
- •Дифференциальные уравнения
- •Основные понятия:
- •Признаки сходимости ряда:
- •Ряды по степени разности
- •Теория вероятностей
- •Основные понятия теории вероятностей
- •Классическое определение вероятности
- •Геометрические вероятности
- •Алгебра событий
- •Теорема сложения вероятностей двух несовместимых событий
- •Теорема умножения вероятностей.
- •Теорема сложения вероятностей совместимых событий
- •Формула полной вероятности
- •Теорема умножения вероятностей независимых событий:
- •Дискретные случайные величины
- •Закон распределения дискретных случайных величин
- •Функция распределения случайной величины
- •Нормальное распределение
- •Числовые характеристики случайных величин
- •Свойства математического ожидания (мо) дискретной случайной величины:
- •Дисперсия дискретной случайной величины
- •Среднее квадратичное отклонение (стандартное)
- •Системы двух случайных величин и их числовые характеристики
- •Литература
Непрерывность функции
Определение.
Функция
,
определенная на интервале
![]() ,
называется непрерывной в точке
,
называется непрерывной в точке
![]() ,
если
,
если
![]() (т.е. предел функции равен ее значению
при предельном значении аргумента).
(т.е. предел функции равен ее значению
при предельном значении аргумента).
Свойства непрерывных функций:
Если функции и
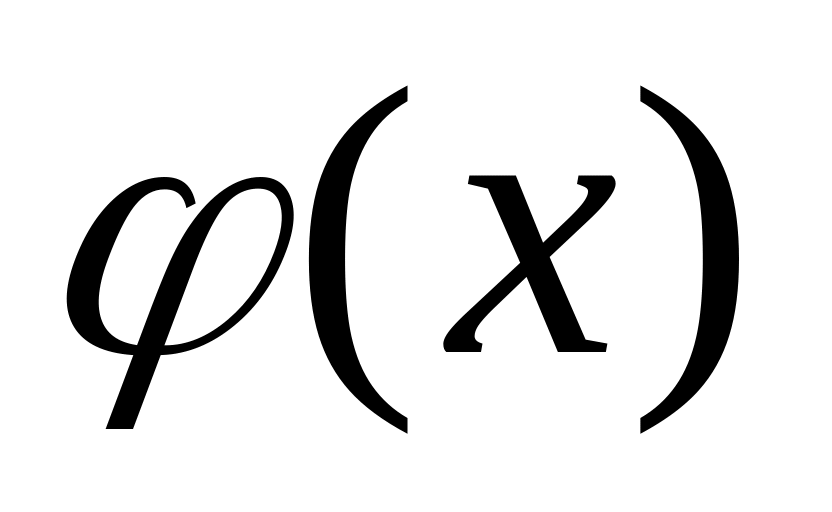 непрерывна в
непрерывна в
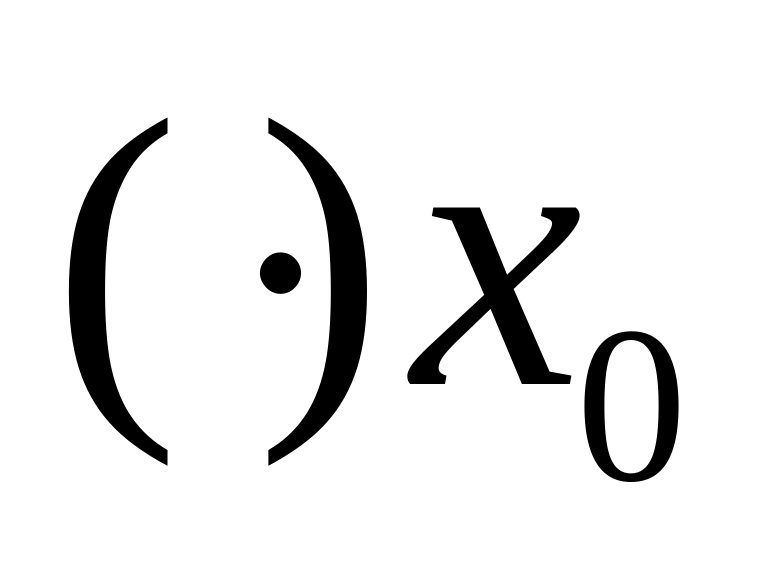 ,
то также непрерывны в этой точке их
сумма
,
то также непрерывны в этой точке их
сумма
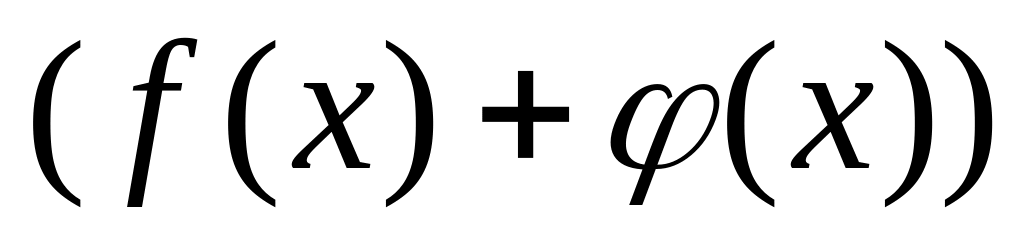 ,
разность
,
разность
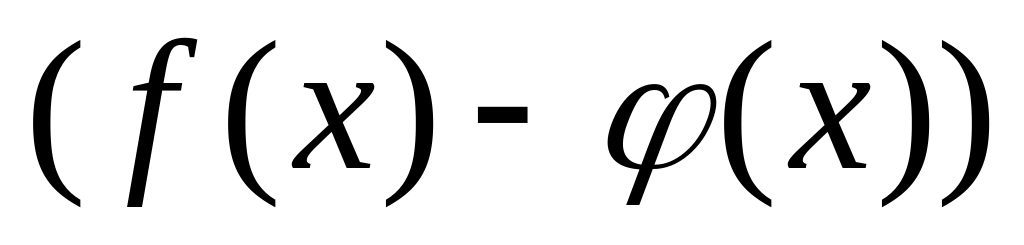 ,
произведение
,
произведение
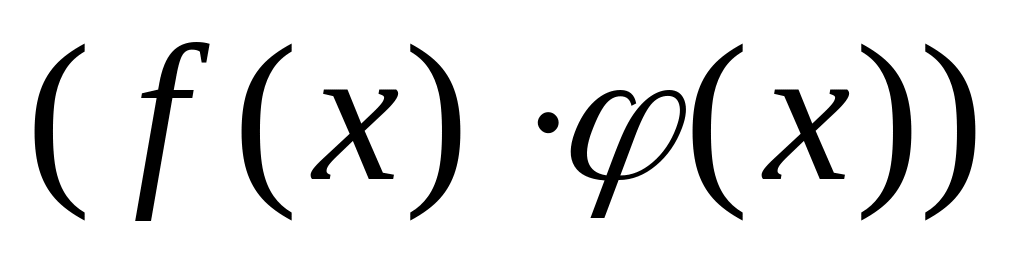 ,
а также частное
,
а также частное
 при условии, что
при условии, что
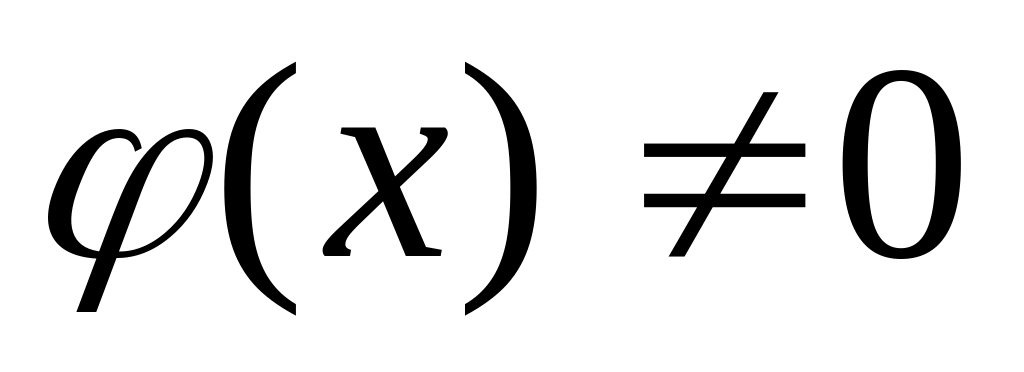 .
.Если функция непрерывна в точке
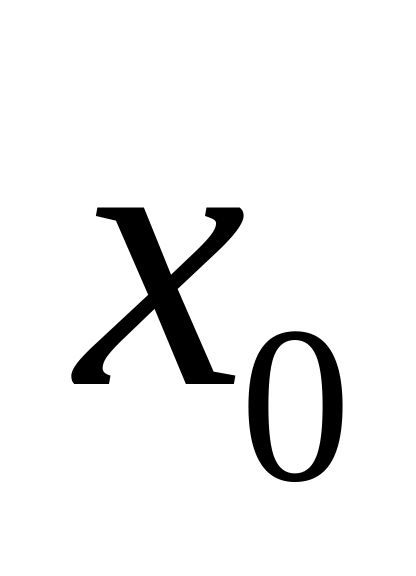 ,
а функция
,
а функция
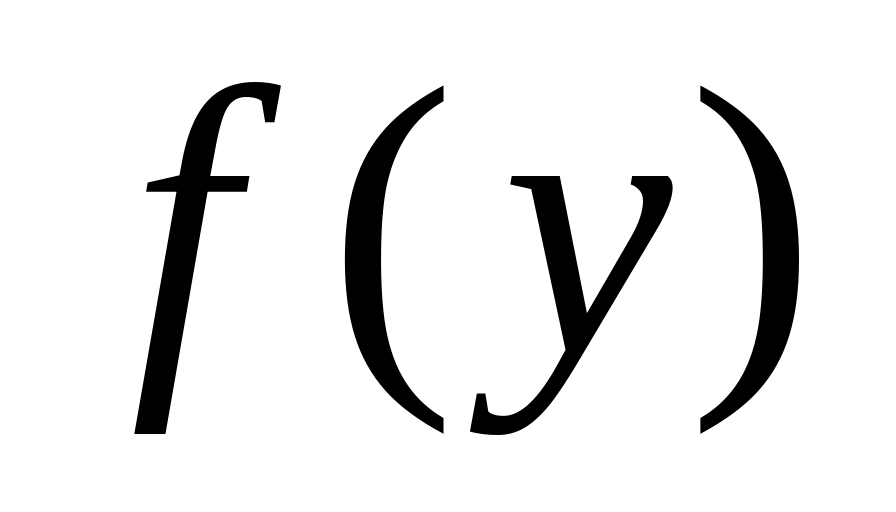 непрерывна в точке
непрерывна в точке
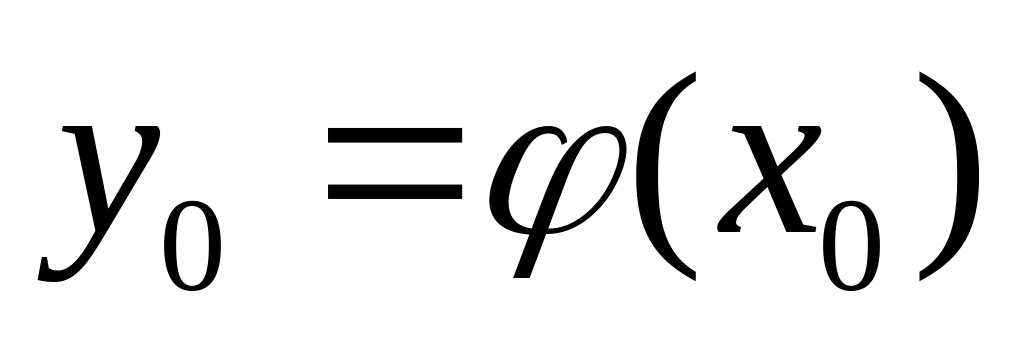 ,
то сложная функция
,
то сложная функция
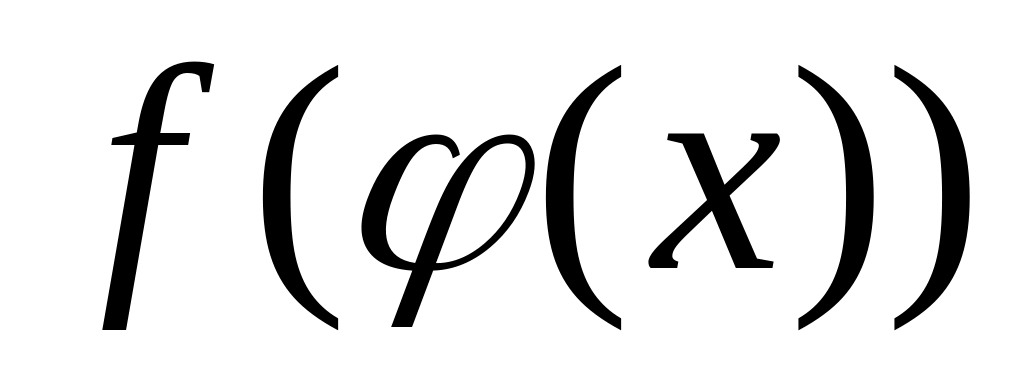 непрерывна в
.
непрерывна в
.Функция называется непрерывной на интервале , если она на нем определена и непрерывна в каждой точке этого интервала.
Все элементарные функции непрерывны в соответствующей области определения.
Точки разрыва функции:
Рассмотрим
функцию
,
определенную на интервале
,
кроме, быть может, точки
.
Значение аргумента
называется точкой
разрыва,
если при
![]() функция определена, но не является
непрерывной или не определена при этом
значении
.
Если
имеет точку разрыва и существуют пределы
слева и справа, то это точка
разрыва первого рода.
Если пределы справа и слева равны, то
– точка
устранимого разрыва.
Если хотя бы один предел не существует
или является бесконечным, то
– разрыв
второго рода.
функция определена, но не является
непрерывной или не определена при этом
значении
.
Если
имеет точку разрыва и существуют пределы
слева и справа, то это точка
разрыва первого рода.
Если пределы справа и слева равны, то
– точка
устранимого разрыва.
Если хотя бы один предел не существует
или является бесконечным, то
– разрыв
второго рода.
Пример:
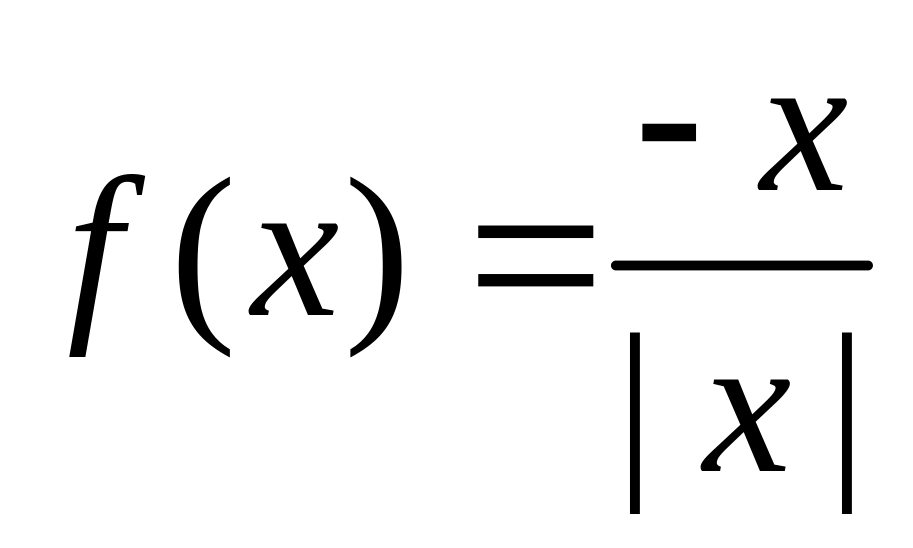 ,
при
,
при
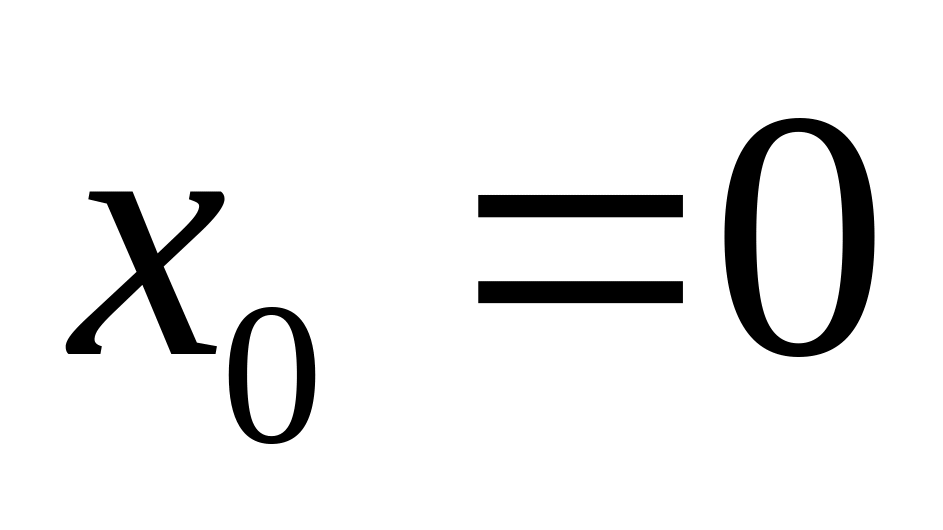 .
.
![]() ,
,
![]() ,
при
,
при
![]() неопределенна и в этой точке пределы
неравны, то это разрыв первого рода.
неопределенна и в этой точке пределы
неравны, то это разрыв первого рода.
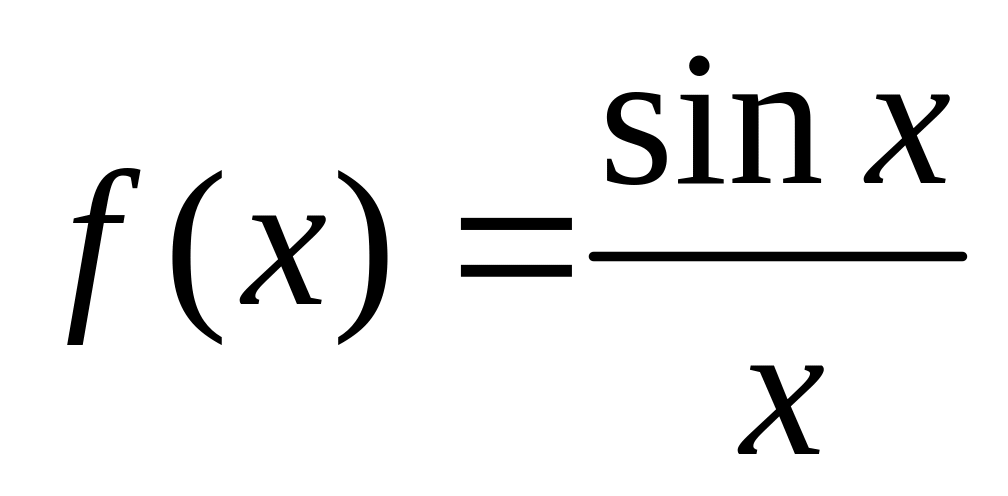 ,
,
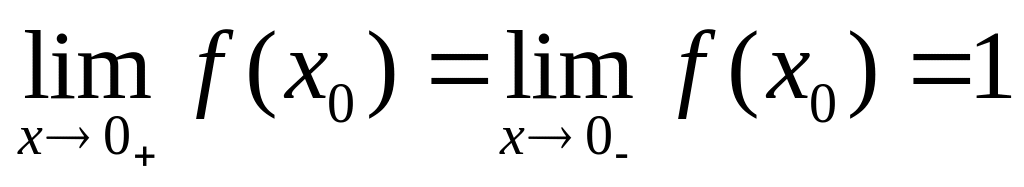 .
Устранимый разрыв.
.
Устранимый разрыв.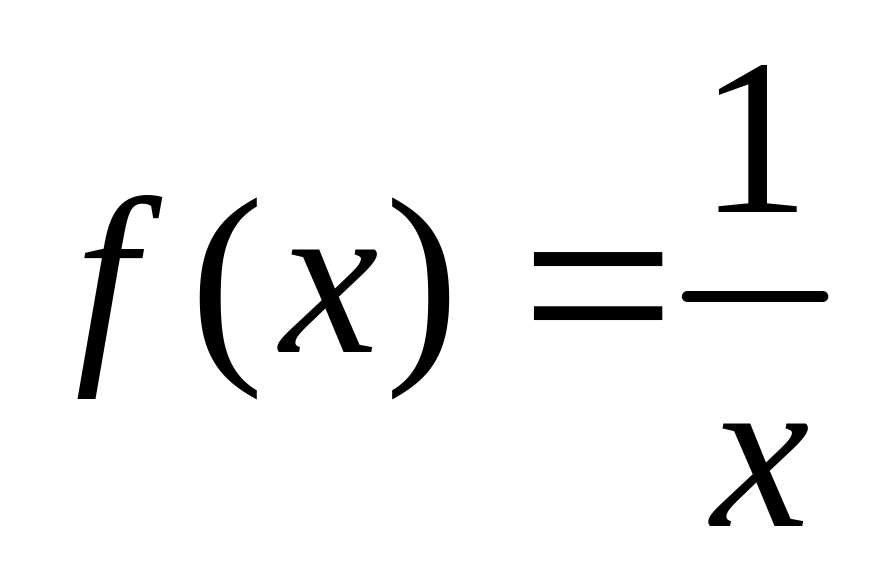 ,
,
,
,
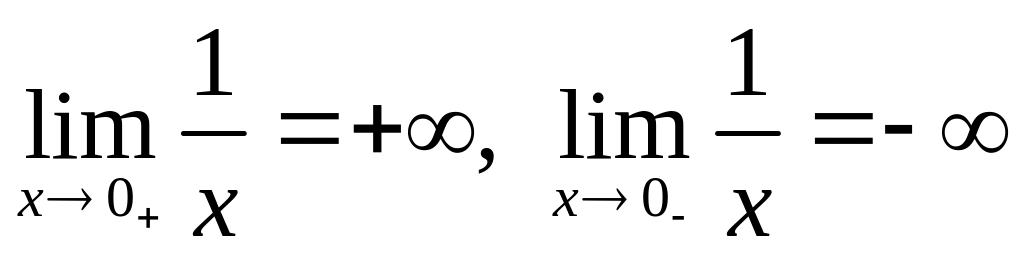 .
Разрыв второго рода.
.
Разрыв второго рода.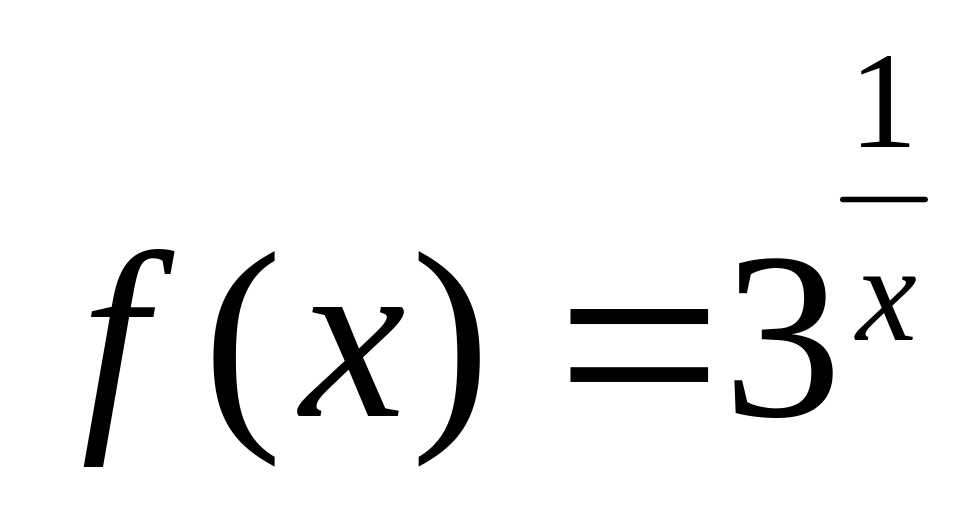 ,
,
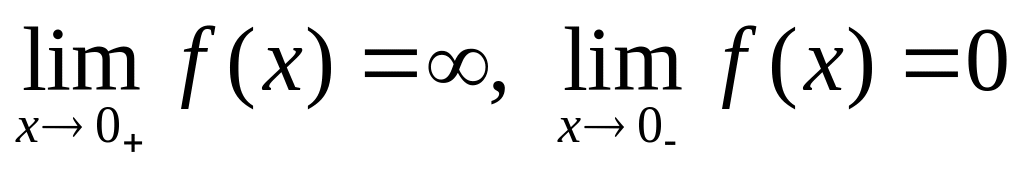 .
Разрыв второго рода.
.
Разрыв второго рода.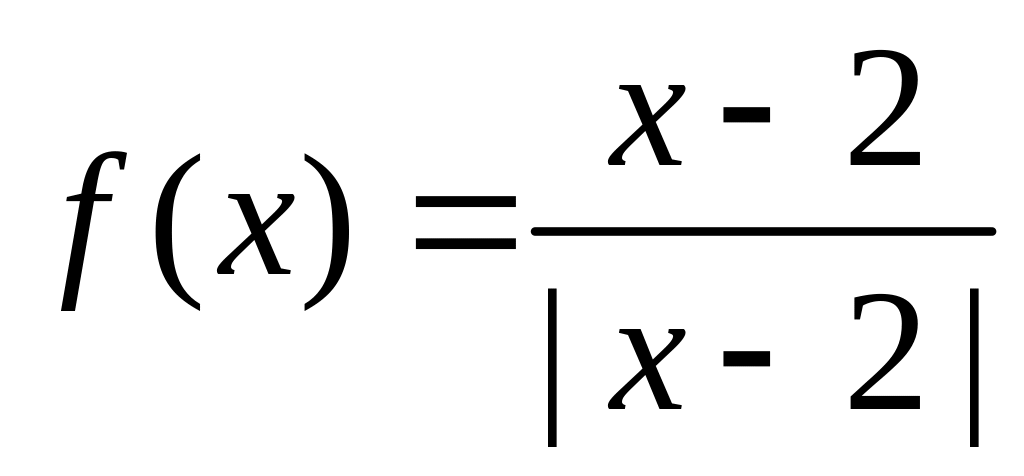 .
Какой разрыв в
.
Какой разрыв в
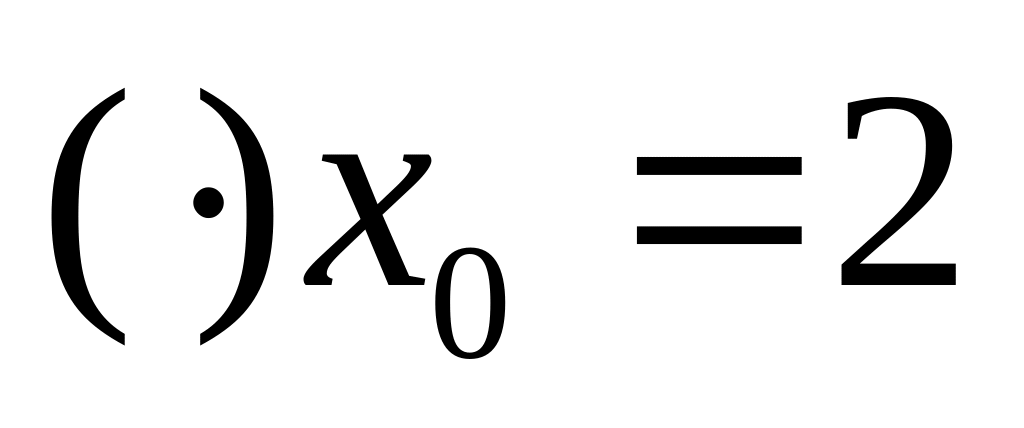 ?
?
![]() .
Разрыв первого рода.
.
Разрыв первого рода.
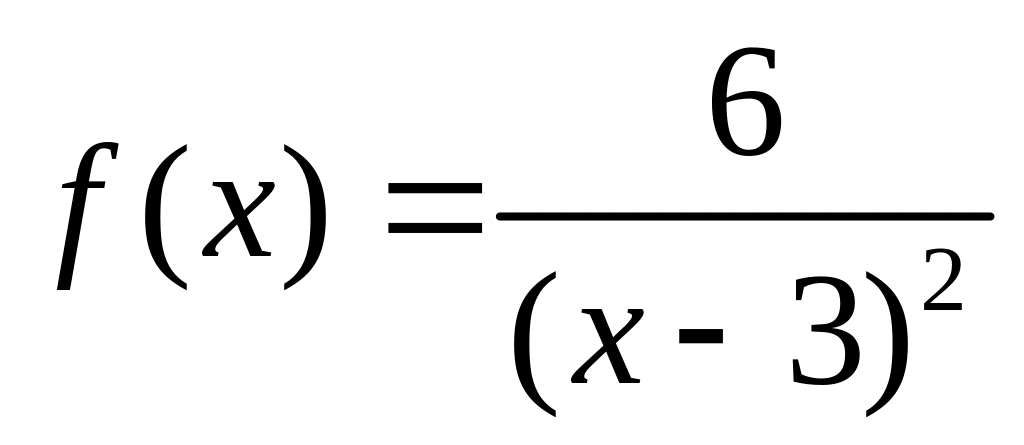 ,
,
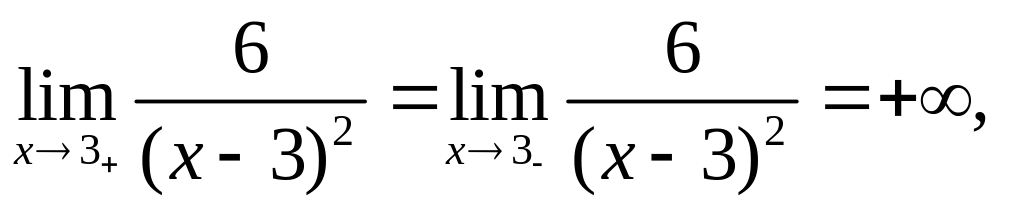 .
Точка разрыва.
.
Точка разрыва.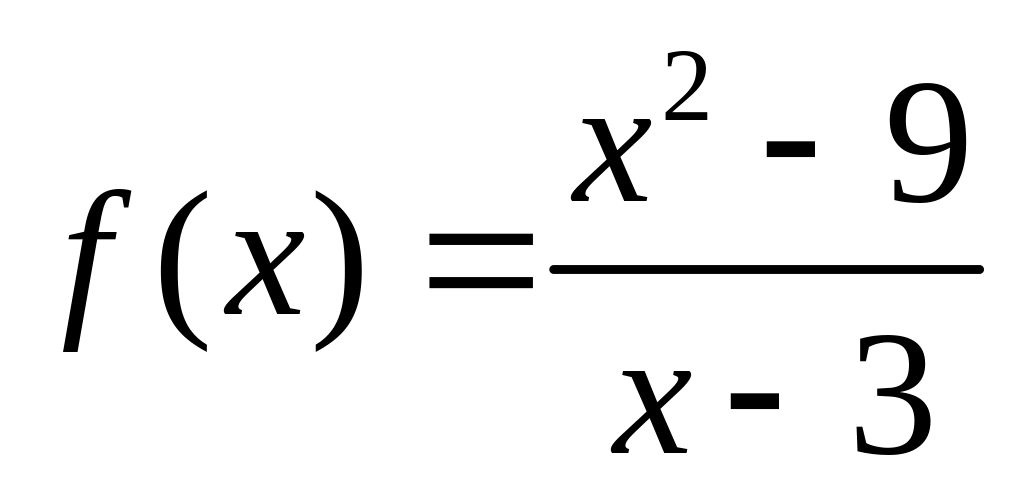 (Устранимый
разрыв при
(Устранимый
разрыв при
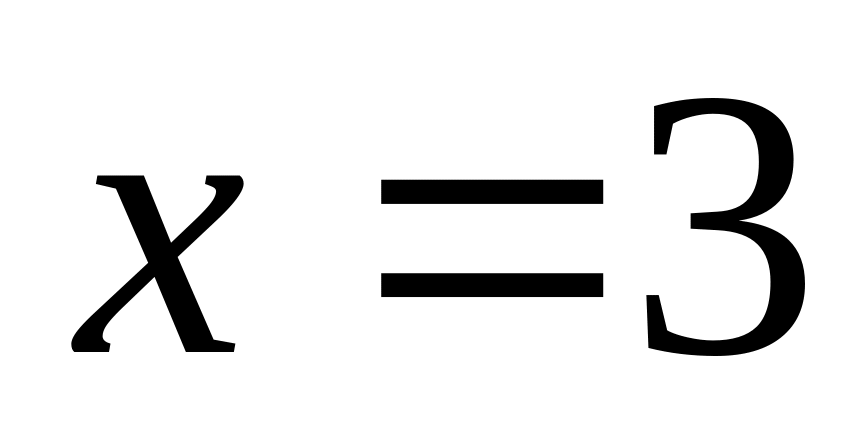 ).
).
Функция разрывна, если нарушается хотя бы одно условие:
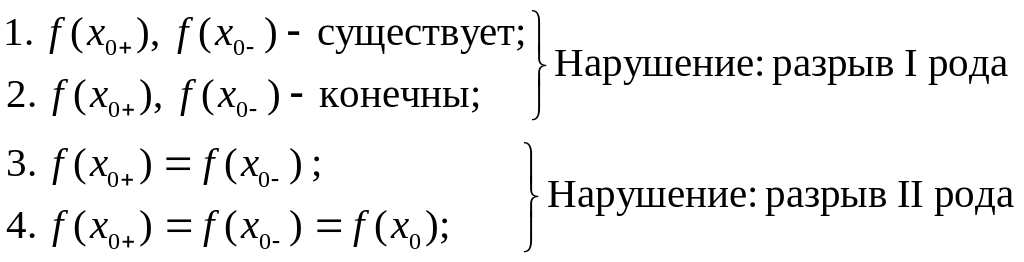
Производная
Определение производной
О пределение:
производной функции
в точке
называется предел отношения приращения
этой функции к приращению аргумента,
когда приращение аргумента стремиться
к нулю.
пределение:
производной функции
в точке
называется предел отношения приращения
этой функции к приращению аргумента,
когда приращение аргумента стремиться
к нулю.
Производная
функции
в точке
обозначается символом
![]() (читается "эф штрих от
")
или
(читается "эф штрих от
")
или
![]() .
.
Действие нахождения производной функции называется ее дифференцированием.
![]() или
или
![]() или
или
![]()
Геометрический
смысл
![]() :
угловой коэффициент касательной к
кривой
при
.
:
угловой коэффициент касательной к
кривой
при
.
Уравнение
касательной:
![]() .
.
Механический
смысл
производной (скорость есть изменение
пусти по времени:
![]() )
)
Правила дифференцирования
Производные высших порядков
Определение.
Производной второго порядка или второй
производной функции
называется производная от ее производной:
![]() или
или
![]() или
или
![]() .
.
Если
![]() ,
то
,
то
![]() ,
,
![]() –
механический смысл второй производной.
–
механический смысл второй производной.
Применение производной для исследования функции
Исследование функций можно провести по следующей схеме:
Найти область определения функции.
Исследовать изменение функции при стремящемся к концам промежутков области определения.
Поверить функцию на четность и нечетность (
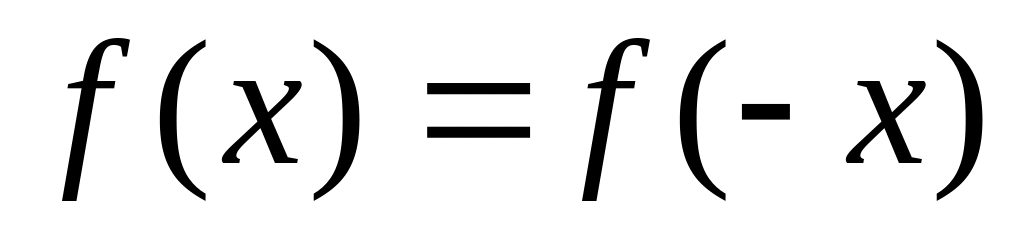 – четная,
– четная,
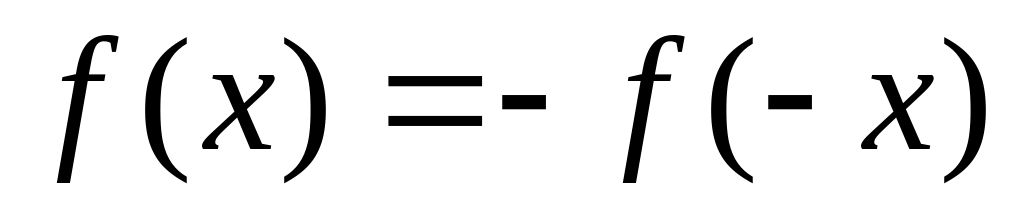 – нечетная;
– нечетная;
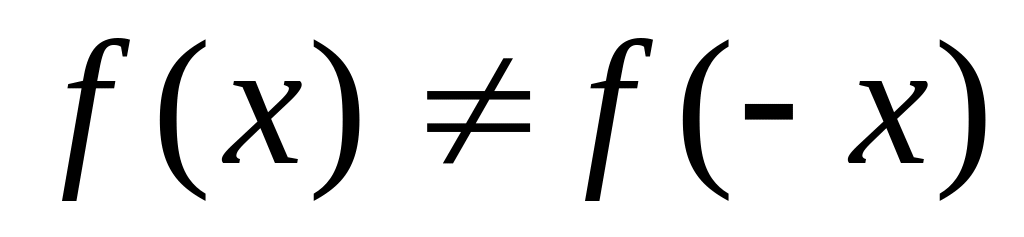 и
и
 – общего вида).
– общего вида).
Проверить, является ли функция периодической.
Найти критические точки (вычислить
 ;
решить уравнение
;
решить уравнение
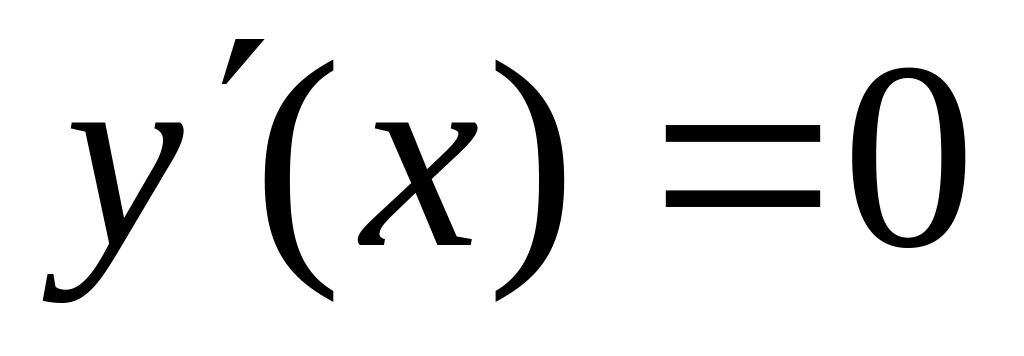 ).
).Найти промежутки возрастания (
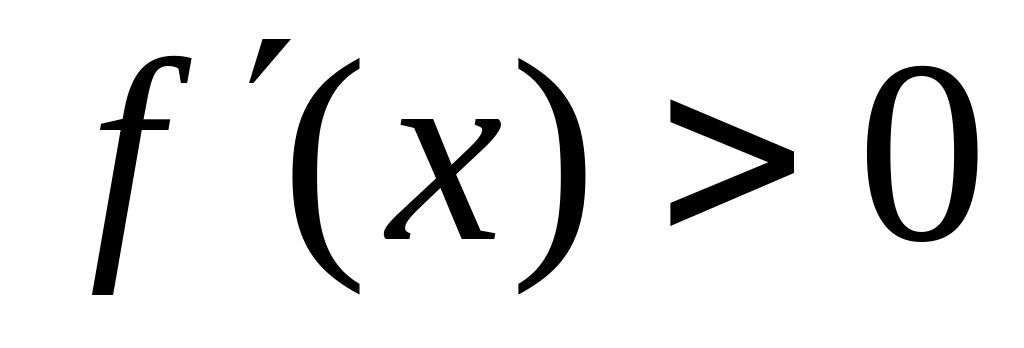 )
и убывания
)
и убывания
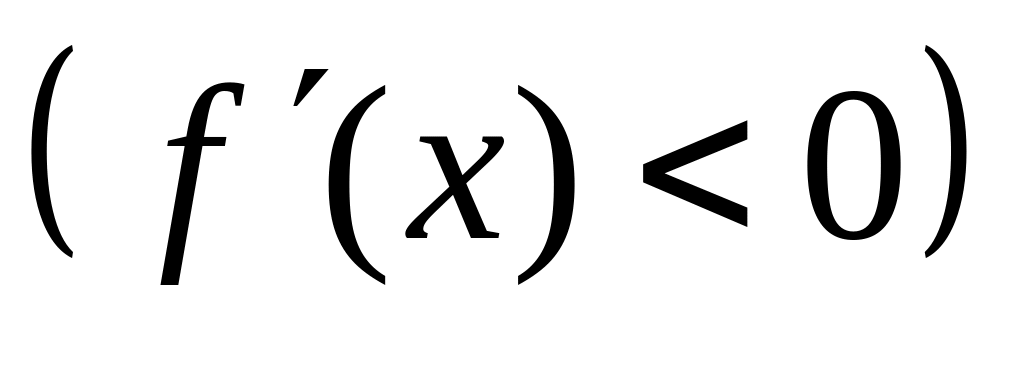 функции.
функции.
Определить точки экстремума, их вид и вычислить значения экстремумов.
Определить интервалы выпуклости (
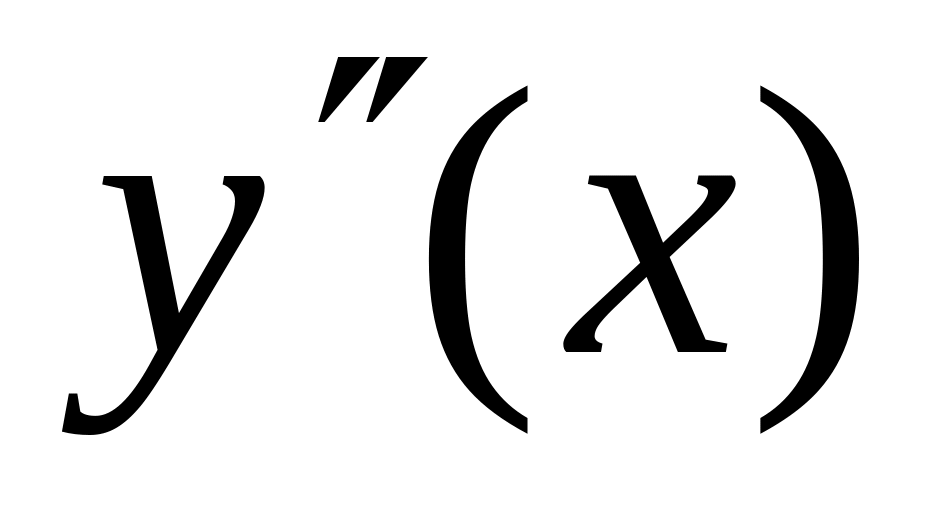 ;
;
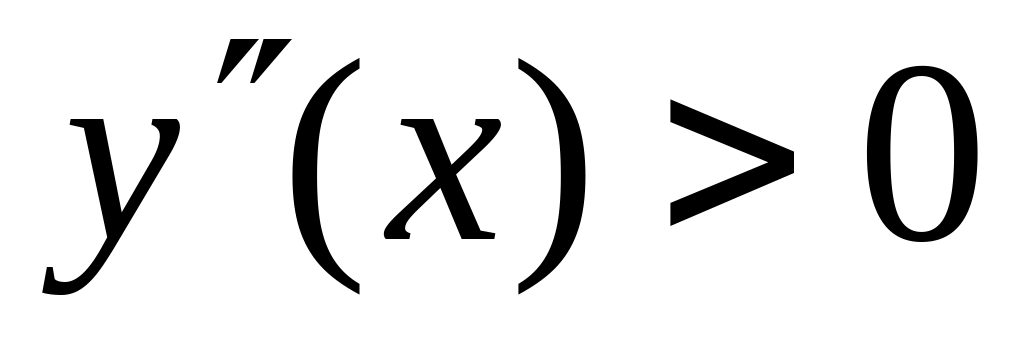 – выпуклая вниз;
– выпуклая вниз;
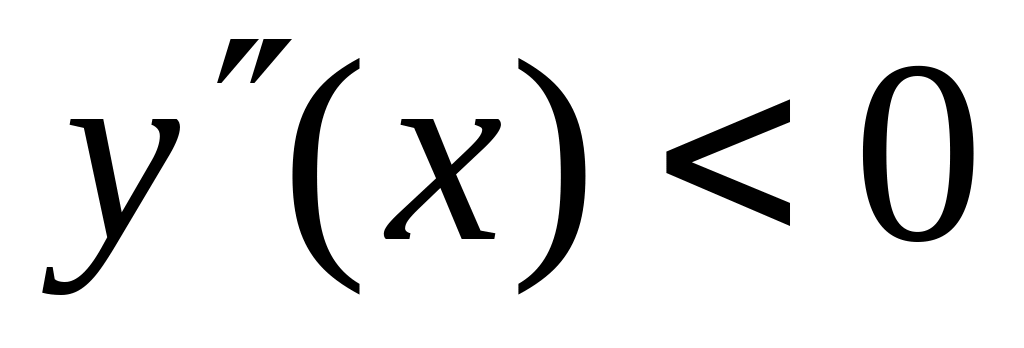 – выпуклая вверх) и точки перегиба (
– выпуклая вверх) и точки перегиба (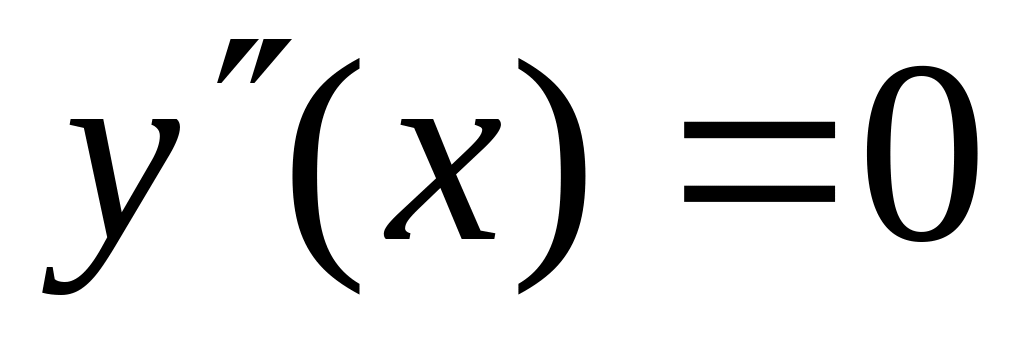 или
не существует).
или
не существует).Найти точки пересечения графика функции с осями координат (
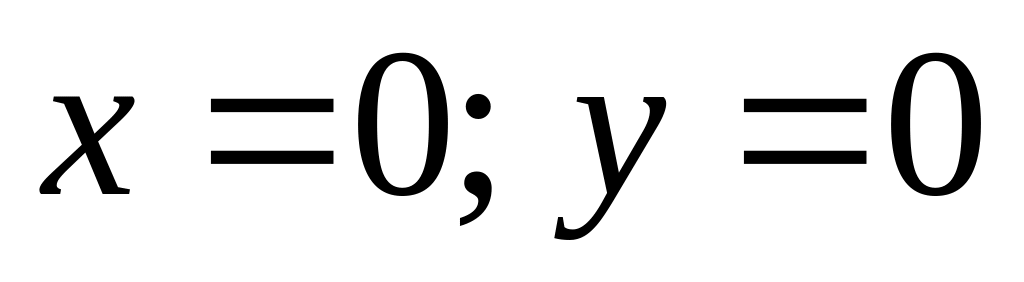 ).
).Вычислить асимптоты кривой если
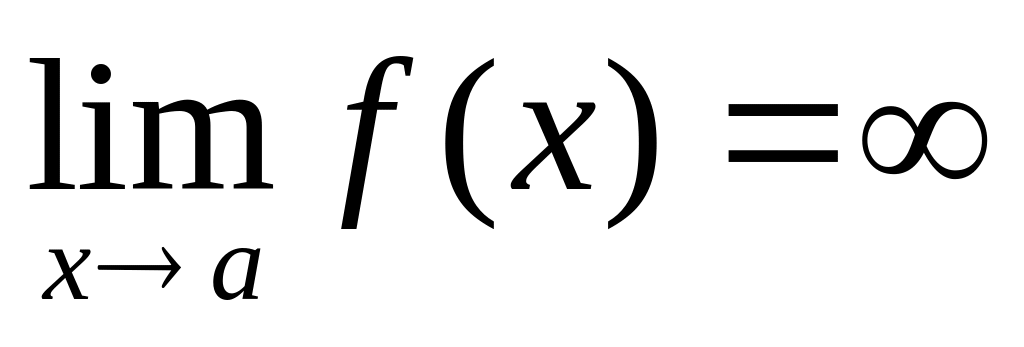 ,
то прямая
,
то прямая
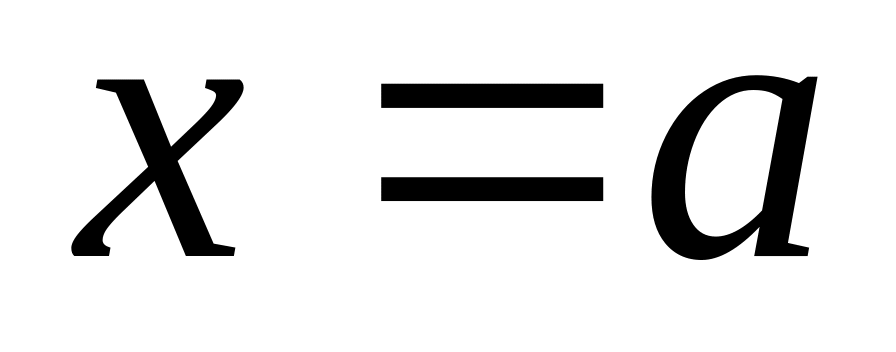 – вертикальная асимптота; если
– вертикальная асимптота; если
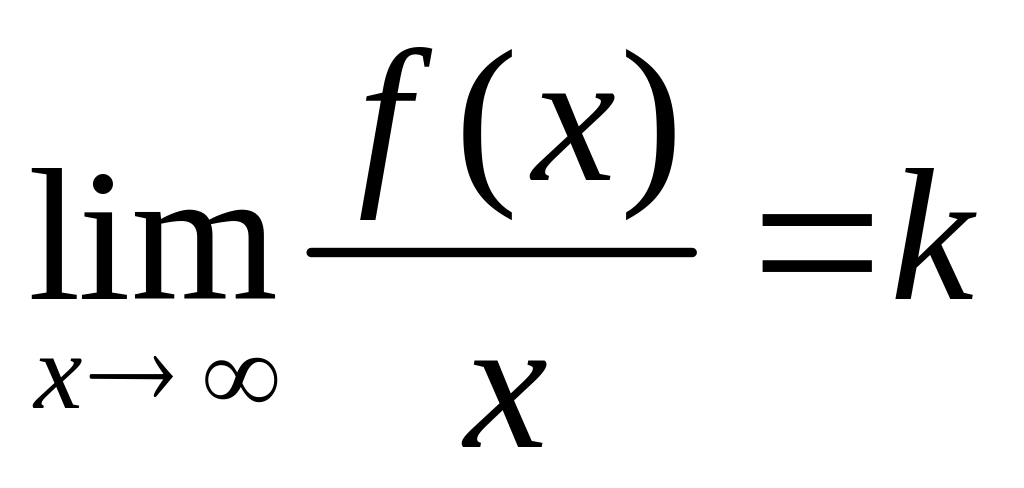 ,
,
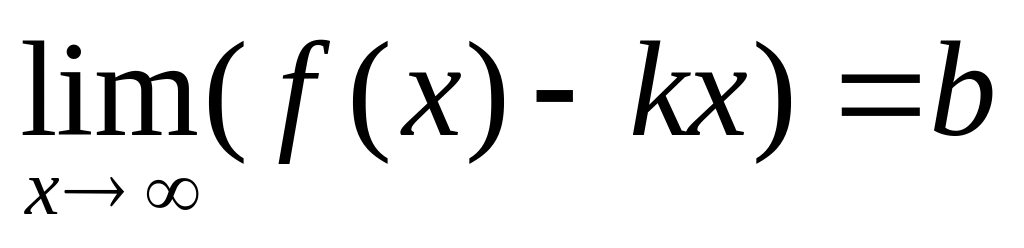 ,
то
–наклонная асимптота.
,
то
–наклонная асимптота.Построить график функции.
Правило
Лопиталя.
Производную можно применять для
нахождения пределов отношений вида
![]() и
и
![]() :
предел отношения двух бесконечо малых
или бесконечно больших функций равен
пределу отношения их производных, если
последний существует:
:
предел отношения двух бесконечо малых
или бесконечно больших функций равен
пределу отношения их производных, если
последний существует:
![]() .
Иногда правило Лопиталя приходится
применять несколько раз.
.
Иногда правило Лопиталя приходится
применять несколько раз.