2. Способы задания функции

Функция (соответствие) может быть задано при помощи формулы – аналитически ( , , и т.д.). Если уравнение, при помощи которого функция задана, записано неявно, то его надо решить относительно и привести функцию к явной форме:

Бывают такие случаи, когда задана несколькими формулами:

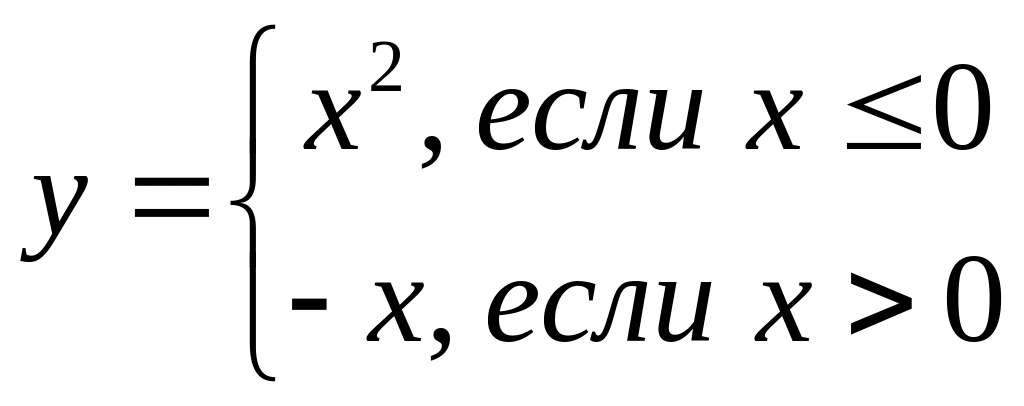
Табличный способ задания функции – способ здания при помощи таблицы (таблица тригонометрических функций, таблица логарифмов).

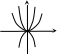
Г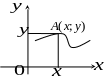 рафический способ задания – способ задания при помощи графика. Графиком называется множество точек плоскости, координаты которых связаны соотношением . Само равенство называется уравнением графика. Чтобы с помощью графика найти значение переменных, надо на графике взять точку и опустить перпендикуляры на оси координат:

3. Обзор элементарных функций и их графиков

Линейная функция. Функция вида называется линейной, где – угловой коэффициент, – свободный член.

График линейной функции – прямая линия. Чтобы построить прямую, надо взять две точки, принадлежащие прямой: через две точки плоскости проходит прямая и притом только одна.

Дробно-линейная функция. Такая функция задается отношением двух многочленов: .

Примером такой функции является функция . Графиком такой функции является гипербола.

Степенная функция – функция вида , где – действительное число. Если , где – натуральное число, то . Запись – корень степени или радикал.

, – биссектриса I и III координатных углов;

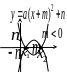
, – парабола, проходящая через начало координат;

, –

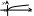
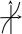, – кубическая парабола.

П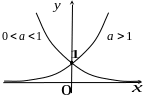 оказательная функция:

, , , .

1. 

2. 

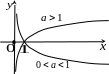
Логарифмическая функция:

, , , .

Функция, обратная данной:

; ; .

Графики симметричны относительно прямой .

Тригонометрические функции:

синусоида

косинусоида

тангенсоида

катангенсоида

Обратные тригонометрические функции

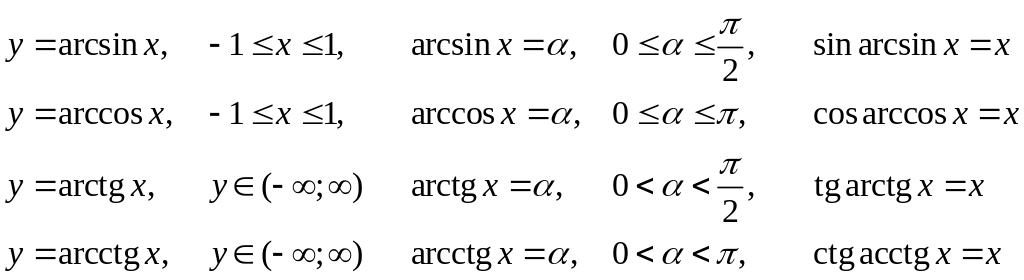
7. Пределы

   1. Предел последовательности

Определение 2: бесконечной числовой последовательностью называется функция , определенная для всех натуральных чисел. – множество элементов последовательности.

– формула

Определение 2: число называется пределом числовой последовательности , если для любого существует номер , зависящий от , что для всех выполняется неравенство .

или , при .

Иллюстрация .

п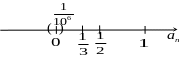 ри , .

Каждая числовая последовательность стремится к своему пределу по-своему.

Отметим, что последовательность может иметь только один предел. Последовательность, имеющая предел, ограничена, т.е. .

Свойства пределов:

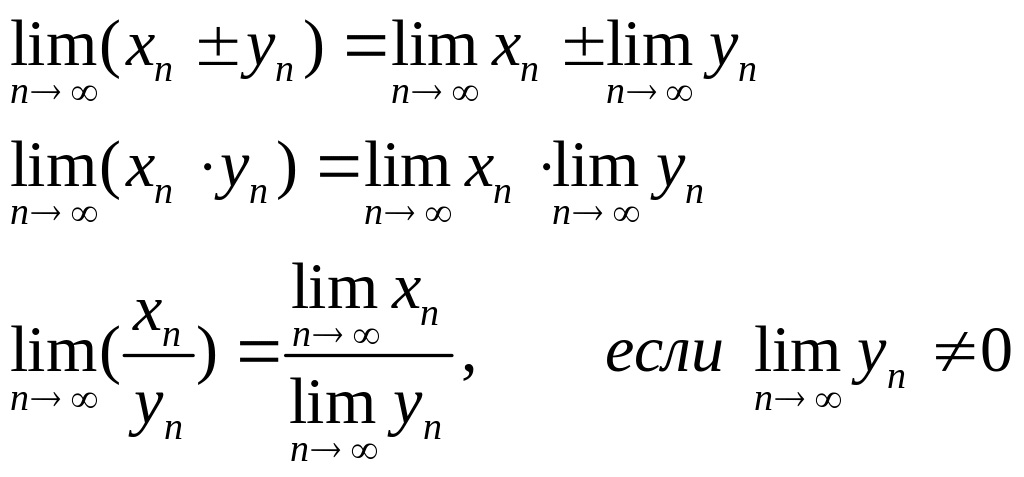
– второй замечательный предел

( – натуральный логарифм)

2. Предел функции

Определение1: Число называется пределом функции , если для любого числа существует (дельта от эпсилон), что для всех , удовлетворяющих условию выполняется неравенство .

или при .

И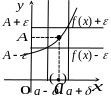 ллюстрация:

Замечательные пределы:

Первый замечательный предел: (при значение функции )

Второй замечательный предел: (иррациональное число )

Способы нахождения пределов

1. Подстановка в данное выражение предельного значения аргумента:

   1. 

   2. 

2. Предел числителя не равен нулю ( 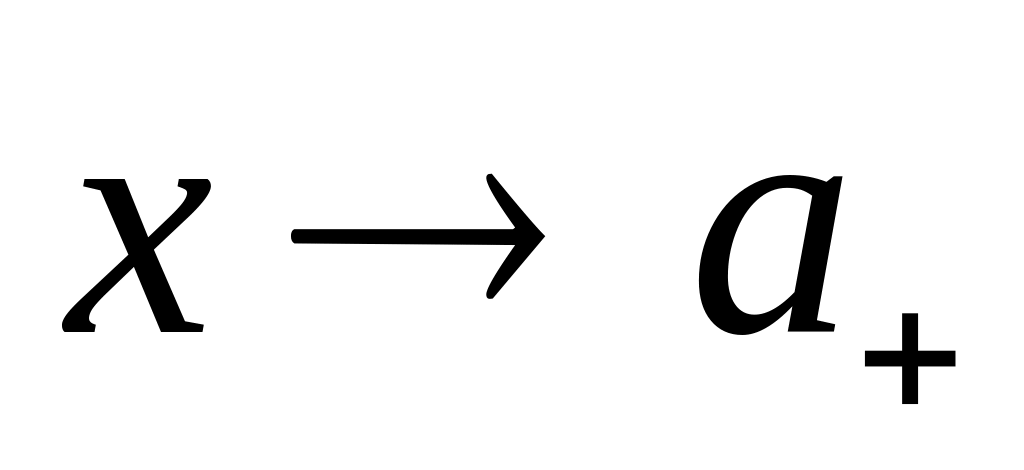справа и 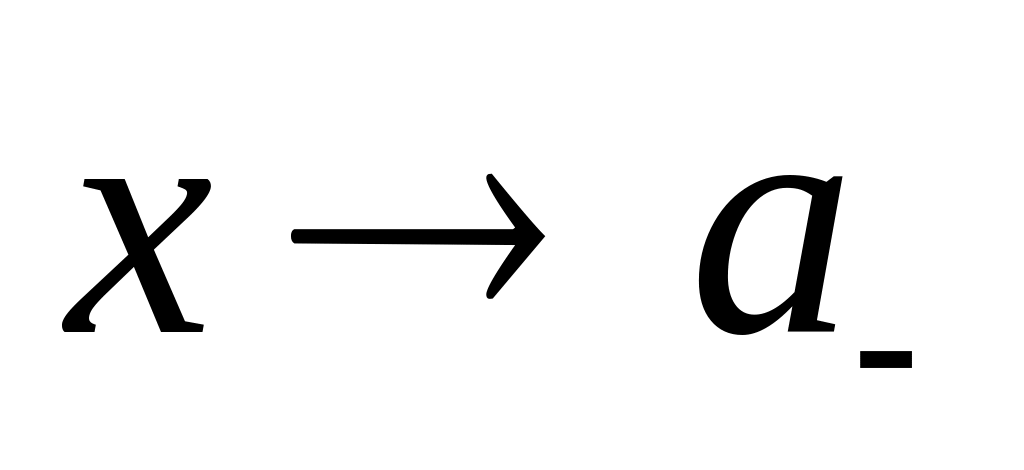слева):

рассматриваем

при и , то

е сли и , то

3. Предел числителя равен нулю:

(упрощение выражений, стоящих под знаком предела)

4. Вычисление предела при :

(почленное деление на в наибольшей степени)