
- •1. Аксиоматика 3
- •2. Множества 4
- •3. Аналитическая геометрия 14
- •4. Векторная алгебра 25
- •5. Матрицы и определители 30
- •Аксиоматика
- •Аксиоматический метод построения математики
- •Математический язык
- •Множества
- •Понятие множества
- •Пустое множество
- •Числовые множества
- •Подмножества
- •Пересечение множеств
- •Объединение множеств
- •Вычитание множеств
- •Аналитическая геометрия
- •Система координат на плоскости и в пространстве
- •Расстояние между двумя точками на плоскости
- •Уравнение линии. Уравнение прямой с угловым коэффициентом
- •Уравнение – уравнение прямой с угловым коэффициентом k
- •Общее уравнение прямой
- •Уравнение прямой в отрезках
- •Уравнение прямой, проходящей через данную точку в данном направлении
- •Уравнение прямой, проходящей через данную точку
- •Уравнение прямой, проходящей через две данные (различные) точки и
- •Полярные координаты
- •Угол между прямыми
- •Уравнение окружности
- •Эллипс. Каноническое уравнение эллипса
- •Гипербола. Каноническое уравнение гиперболы
- •Парабола. Каноническое уравнение параболы
- •У равнение сферы
- •Векторная алгебра
- •Понятие вектора
- •Коллинеарные векторы
- •Операции над векторами
- •Угол между векторами
- •Проекция вектора на ось
- •Скалярное произведение двух векторов
- •Координаты вектора
- •Разложение векторов
- •Действия над векторами, заданным координатами в пространстве
- •Матрицы и определители
- •Матрицы
- •Определители
- •Определители третьего порядка
- •Миноры и алгебраические дополнения матрицы
- •Обратная матрица
- •Системы линейных уравнений
- •Формулы Крамера
- •Матричный способ решения систем линейных уравнений
- •Метод Гаусса
- •Функции
- •Понятие функции
- •Способы задания функции
- •Обзор элементарных функций и их графиков
- •Пределы
- •Предел последовательности
- •Предел функции
- •Непрерывность функции
- •Производная
- •Определение производной
- •Правила дифференцирования
- •Производные высших порядков
- •Применение производной для исследования функции
- •Неопределенный интеграл
- •Способы интегрирования
- •О пределенный интеграл
- •Дифференциальные уравнения
- •Основные понятия:
- •Признаки сходимости ряда:
- •Ряды по степени разности
- •Теория вероятностей
- •Основные понятия теории вероятностей
- •Классическое определение вероятности
- •Геометрические вероятности
- •Алгебра событий
- •Теорема сложения вероятностей двух несовместимых событий
- •Теорема умножения вероятностей.
- •Теорема сложения вероятностей совместимых событий
- •Формула полной вероятности
- •Теорема умножения вероятностей независимых событий:
- •Дискретные случайные величины
- •Закон распределения дискретных случайных величин
- •Функция распределения случайной величины
- •Нормальное распределение
- •Числовые характеристики случайных величин
- •Свойства математического ожидания (мо) дискретной случайной величины:
- •Дисперсия дискретной случайной величины
- •Среднее квадратичное отклонение (стандартное)
- •Системы двух случайных величин и их числовые характеристики
- •Литература
Системы линейных уравнений
Определение
1: линейным
уравнением с
переменными называется равенство вида:
![]() ,
где
,
где
![]() и
числа, одновременно не равные 0.
и
числа, одновременно не равные 0.
Определение 2: системой линейных уравнений с неизвестными называется совокупность линейных уравнений с переменными вида:

Числа
называются коэффициентами
системы
(они берутся со своими знаками).
![]() – свободные
члены.
– свободные
члены.
Если
![]() ,
то система называется однородной.
,
то система называется однородной.
Определение 3: Решить систему уравнений значит найти такие значения неизвестных, при подстановке которых во все уравнения получаются тождества (всегда верные равенства). Однородная система имеет решение, равное 0, но может иметь и другие.
Система, имеющая хотя бы одно решение, называется совместной, система, не имеющая решений, называется несовместной.
Определение 4: Определителем системы линейных уравнений с неизвестными называется
 ;
;
Определитель
![]() получается, если i-ый
столбец заменить столбцом свободных
членов:
получается, если i-ый
столбец заменить столбцом свободных
членов:
 .
.
Формулы Крамера
Швейцарский математик Георг Крамер (1704-1752) вывел следующие формулы решения систем линейных уравнений с неизвестными:
составляем определитель системы
 ,
если
,
если
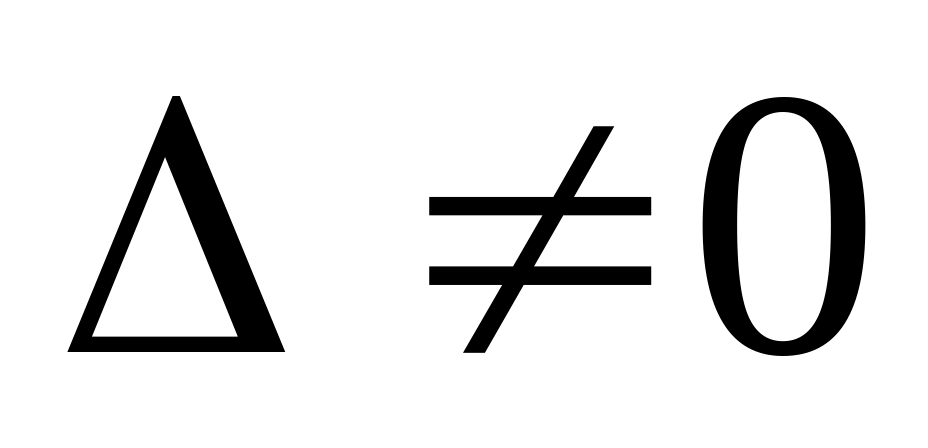 ;
;составляем вспомогательные определители ;
применяем формулы:
![]() ,
,
![]() ,
и т.д.
,
и т.д.
![]() .
.
Если
![]() ,
то система либо несовместная, либо
неопределенная, имеющая бесчисленное
множество решений.
,
то система либо несовместная, либо
неопределенная, имеющая бесчисленное
множество решений.
Матричный способ решения систем линейных уравнений
Сущность матричного способа решения систем линейных уравнений состоит в том, что составляется три матрицы
;  ;
;  .
.
Можем
составить матричное уравнение
![]() откуда
откуда
![]() ,
,
где
– обратная матрица, а
,
![]() ,
,
![]() – решения системы.
– решения системы.
Правило:
составляем матрицы ,
 и
;
и
;если
 ,
то составляем
– обратную матрицу;
,
то составляем
– обратную матрицу;выполнив умножение и получаем , элементы которой – решение системы.
Метод Гаусса
Систему
линейных уравнений с
неизвестными
,
,
…,
![]() можно решить методом исключения
неизвестных. Если
можно решить методом исключения
неизвестных. Если
![]() ,
то умножая первое уравнение на
,
то умножая первое уравнение на
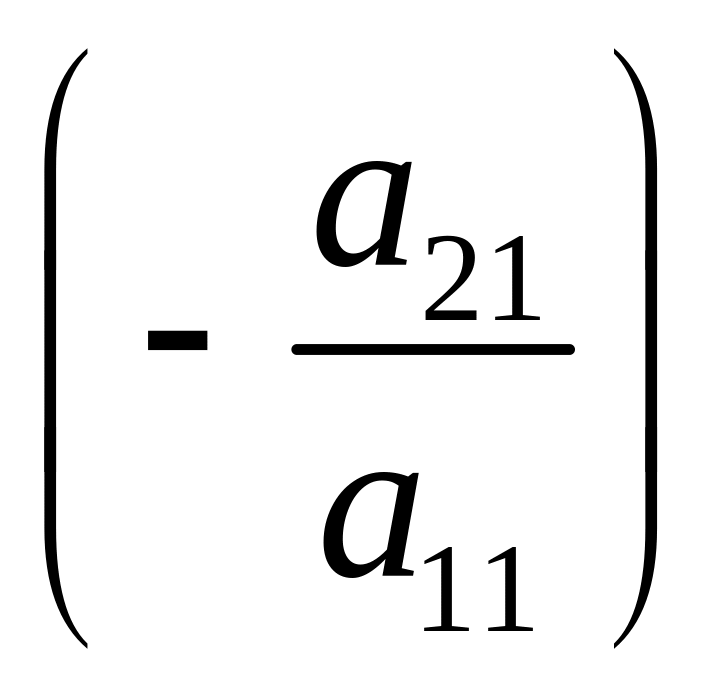 и прибавляя ко второму, получаем
уравнение, которое не содержит
.
Умножая первое уравнение на
и прибавляя ко второму, получаем
уравнение, которое не содержит
.
Умножая первое уравнение на
 и прибавляя к третьему получаем
уравнение, также не содержащее
.
Аналогичным путем преобразуем все
остальные уравнения, в результате чего
придем к системе, эквивалентной исходной,
но не содержащей в
и прибавляя к третьему получаем
уравнение, также не содержащее
.
Аналогичным путем преобразуем все
остальные уравнения, в результате чего
придем к системе, эквивалентной исходной,
но не содержащей в
![]() уравнении
.
Полагая
уравнении
.
Полагая
![]() и проводя аналогичные преобразования
получим систему эквивалентную исходной,
но в
уравнение не содержащую
.
Выполнив ряд аналогичных действий,
получим, что в последнем уравнении
содержится только
.
Таким образом,
– находим из последнего уравнения,
и проводя аналогичные преобразования
получим систему эквивалентную исходной,
но в
уравнение не содержащую
.
Выполнив ряд аналогичных действий,
получим, что в последнем уравнении
содержится только
.
Таким образом,
– находим из последнего уравнения,
![]() – из предпоследнего, и т.д., а
– из первого.
– из предпоследнего, и т.д., а
– из первого.
Метод последовательного исключения неизвестных применим к любой системе линейных уравнений.
Функции
Понятие функции
Определение.
Соответствие, при котором каждому
значению переменной
ставится в соответствие одно
определенное
значение переменной
называется
функцией от
.
Обозначается
![]() или
или
![]() .
.
Переменная называется независимой переменной или аргументом. Совокупность всех значений аргумента , для которых функция определена, называется областью определения этой функции. Совокупность всех значений, которые принимает , называется областью значений функции .
