6. Определители

Определение: определителем или детерминантом второго порядка, соответствующим матрицы , называется запись вида .

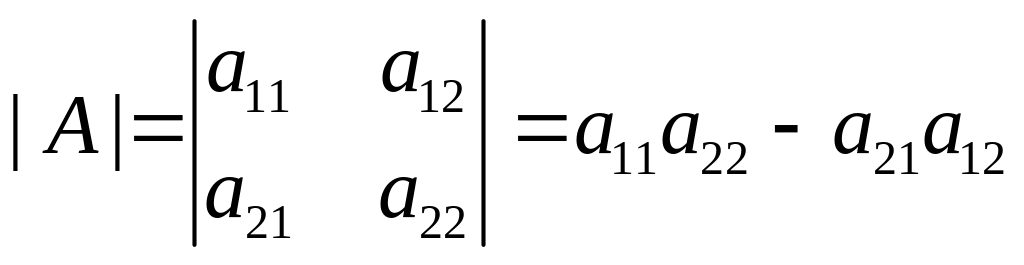Элементы матрицы называются элементами определителя . Элементы образуют главную диагональ, а элементы – побочную.

Для вычисления определителя второго порядка надо из произведения элементов главной диагонали, вычесть произведение элементов, стоящих на побочной диагонали.

Свойства определителя: величина :

1. не изменяется, если заменить его строки соответствующими столбцами:

.

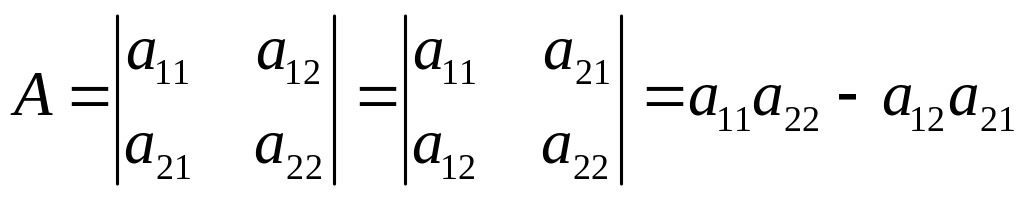2. не меняется, если к элементам какой-либо его строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на одно и тоже число:

3. изменяет знак, если поменять местами его строки или столбцы:

;

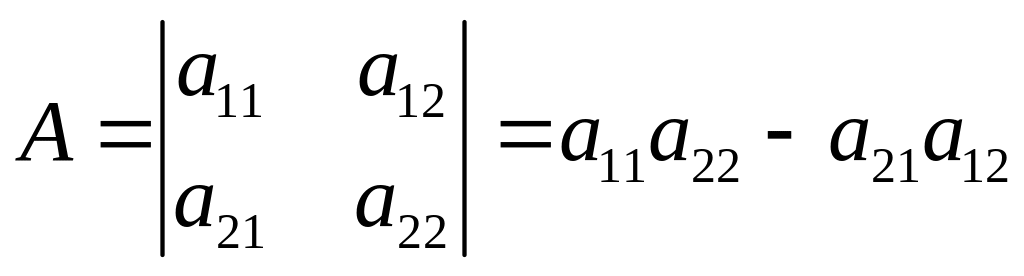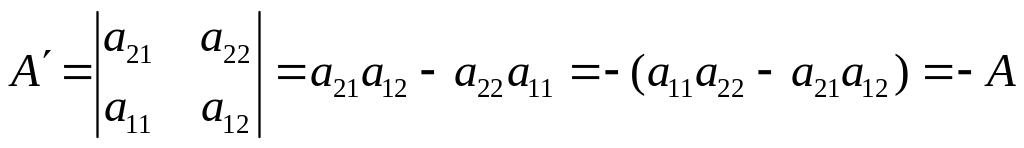
4. увеличиться в раз, если элементы какого-либо его столбца или строки увеличить в раз, т.е. общий множитель, имеющийся в столбце, или строке можно выносить за знак определителя:

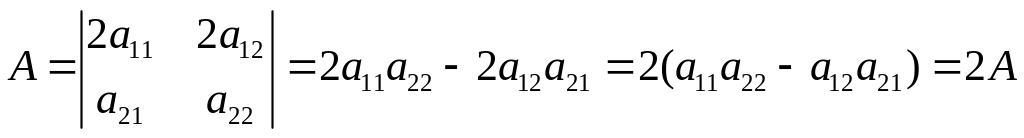
7. Определители третьего порядка

Рассмотрим квадратную матрицу третьего порядка: .

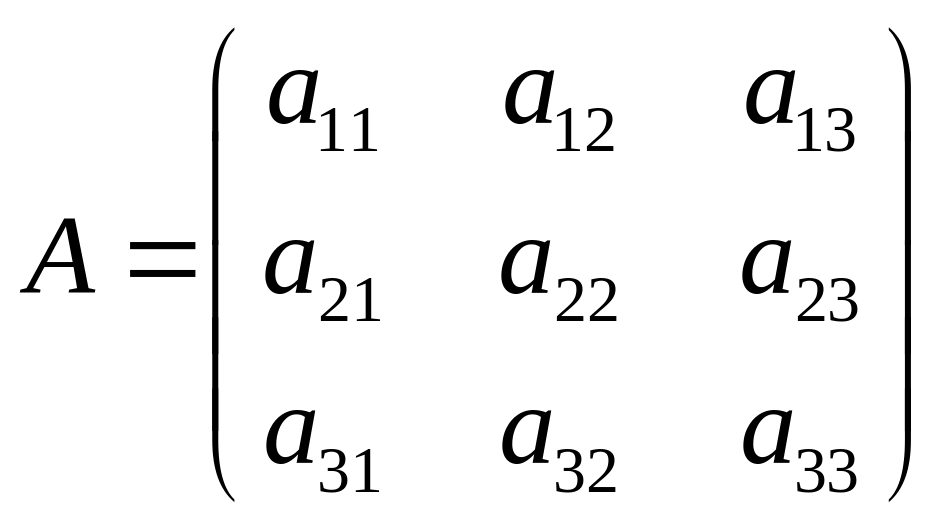Определителем третьего порядка, соответствующей матрице , называется число .

Чтобы запомнить какие произведения брать с "+", а какие с "–" полезно правило треугольников:

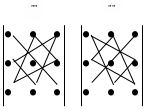
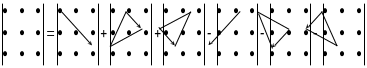
8. Миноры и алгебраические дополнения матрицы

Минором элемента определителя называется определитель, получаемый вычеркиванием из него той строки и того столбца, который данный элемент принадлежит.

Пример:

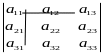
Минор элемента записывается и им является определитель .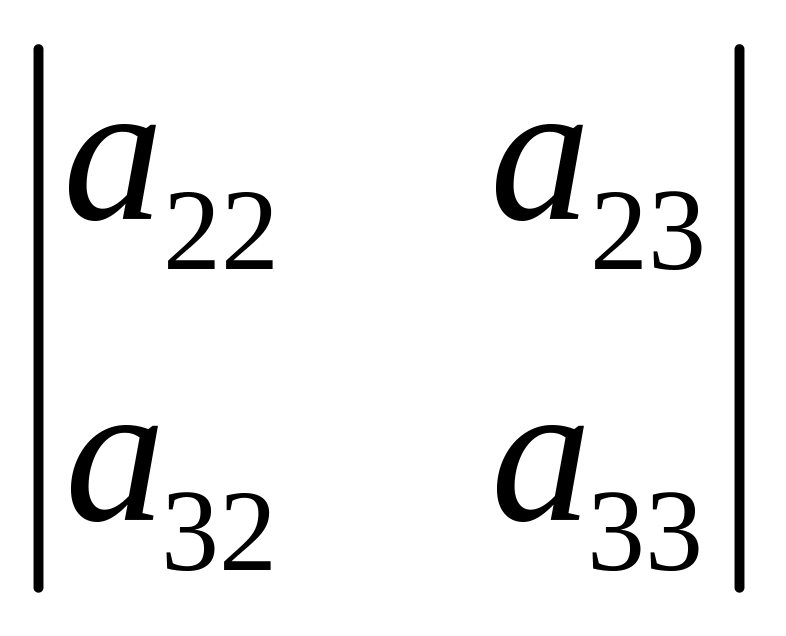

Определение: рангом матрицы называется наибольший из порядков ее миноров, отличных от нуля.

Определение: алгебраическим дополнением элемента ( ) определителя называется его минор, взятый со знаком . Если сумма элементов строки и столбца, на пересечении которого стоит элемент – четная, то "+", если нечетная – то "–": – берутся со знаком "+", – со знаком "–".

Правило: определитель равен сумме произведений элементов какой-либо строки (столбца) на их алгебраическое дополнение: – по этой формуле проводится вычисление определителя методом разложения по элементам первой строки.

9. Обратная матрица

Если – квадратная матрица, то обратной для нее матрицей называется матрица , удовлетворяющая условию , где – единичная матрица .

Если определитель матрицы равен нулю, то матрица называется вырожденной, а если не равен нулю, то матрица называется невырожденной.

Матрица

,

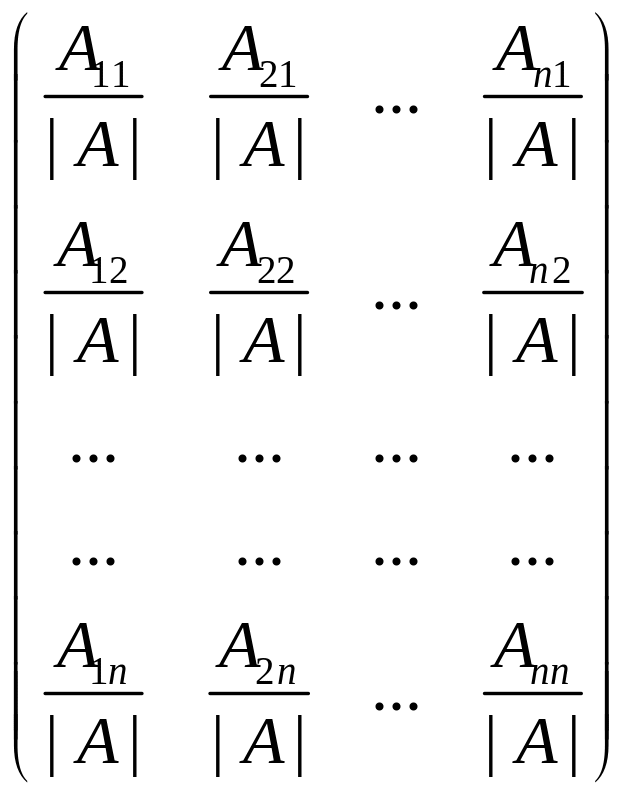где – алгебраическое дополнение элемента невырожденной матрицы, является обратной для .

Рассмотрим пример составления матрицы, обратной данной:

.

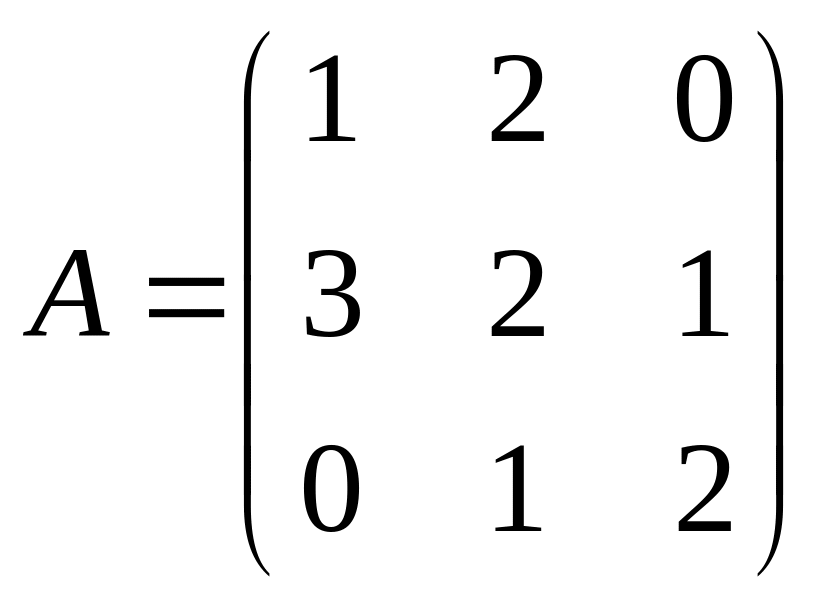1. Вычисляем определитель данной матрицы:

;

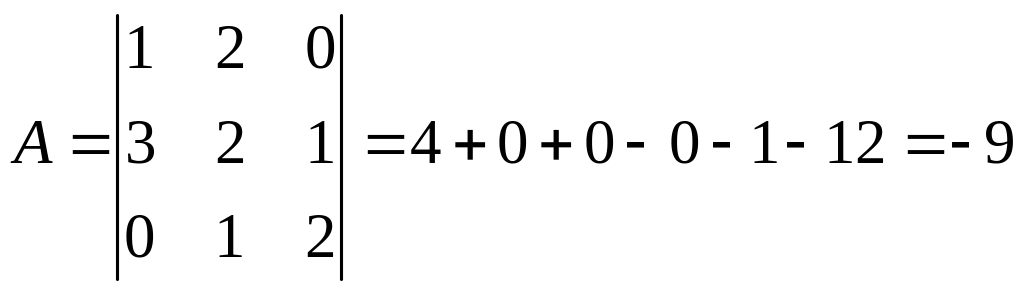2. Вычисляем алгебраические дополнения:

, , ,

, , ,

, , .

3. Составляем матрицу С:

4. Сделав в этой матрице С ее строки столбцами с тем же номером получим:

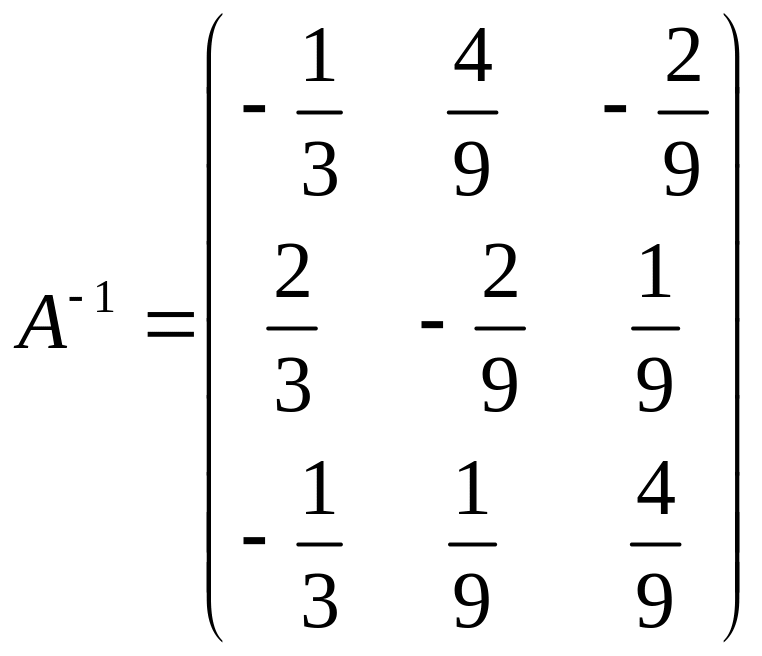– матрица, обратная А.